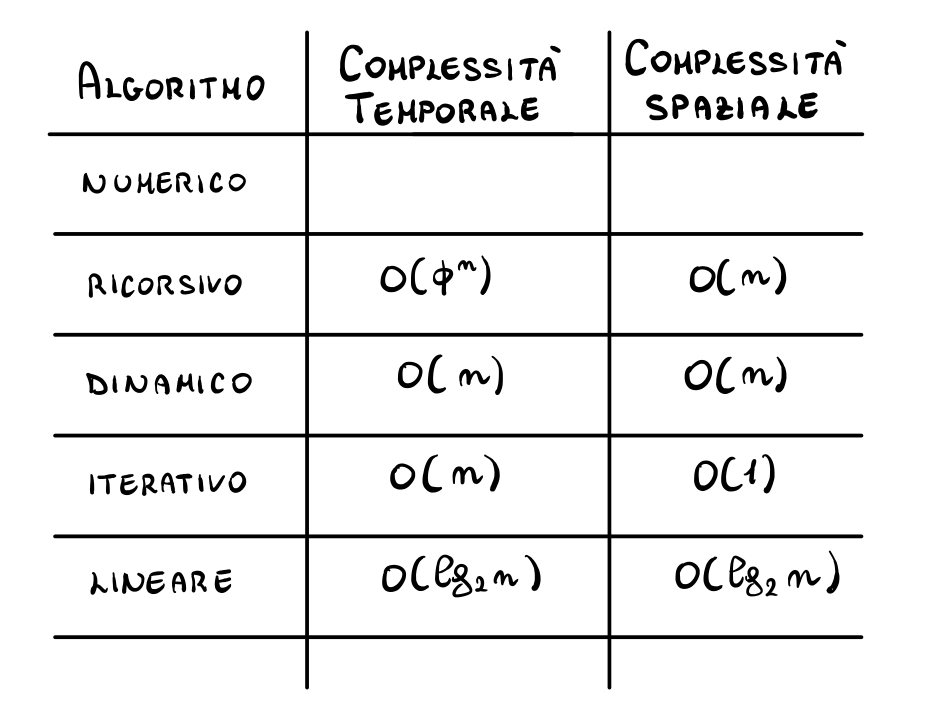
ASD1 - 02 - Numeri di Fibonacci
Lecture Info
Data:
Sito corso: ASD1_2016
Slides: ASD1 - 02 - Numeri di Fibonacci
Introduzione: In questa lezione abbiamo definito la sequenza dei numeri di fibonacci e introdotto cinque diversi algoritmi per calcolare il generico termine della sequenza.
1 Numeri di Fibonacci
I numeri di fibonacci sono stati introdotti da Leonardo Bonacci (1170 \(\approx\) 1250), anche noto come Fibonacci, nel tentativo di trovare una legge matematica che descrivesse la crescita di una popolazione di conigli.
La sequenza è così definita
\[F_n := \begin{cases} F_{n_1} + F_{n-2} \,\,&,\,\, n \geq 3 \\ 1 \,\,&,\,\, n = 1, 2 \\ \end{cases}\]
I primi numeri di questa sequenza sono
\[1,\,\, 1,\,\, 2,\,\, 3,\,\, 5,\,\, 8,\,\, 13,\,\, 21,\,\, 34,\,\, 55,\,\, 89,\,\, 144,\,\, \ldots\]
Andiamo quindi a descrivere vari algoritmi per il calcolo del generico termine della sequenza \(F_n\).
2 Algoritmo Numerico
Un risultato noto rispreso dalla matematica discreta, e in particolare dalla teoria delle funzioni ricorsive, ci dice che
\[\forall n: \,\, F_n = \frac{1}{\sqrt{5}} \cdot \Big(\phi^n - \hat{\phi}^n \Big)\]
dove,
\[\phi := \frac{1 + \sqrt{5}}{2} \approx 1,618\]
\[\hat{\phi} := \frac{1 - \sqrt{5}}{2} \approx -0,618\]
Osservazione: Il valore \(\phi\) è anche noto come rapporto aureo, ed è molto presente in natura.
Un primo possibile algoritmo per il calcolo di \(F_n\) è quindi il seguente

Questo algoritmo però risulta problematico in quanto non è corretto. I numeri \(\phi\) e \(\hat{\phi}\) infatti sono irrazionali, ovvero sono rappresentabili come una sequenza infinita di cifre che non si ripete mai. I calcolatori però hanno una memoria finita, e quindi non sono in grado di memorizzare completamente questi numeri. Possono solo memorizzarne un'approssimazione. L'output ritornato da questo algoritmo quindi, quando viene implementato in un calcolatore, non è sempre corretto.
Consideriamo infatti il seguente algoritmo
def fibo_1(n): phi_1 = (1 + math.sqrt(5))/2 phi_2 = (1 - math.sqrt(5))/2 return 1/math.sqrt(5) * (phi_1**n - phi_2**n)
Quando lo andiamo ad eseguire su vari input otteniamo il seguente risultato
F_0 = 0.0 F_1 = 1.0 F_2 = 1.0 F_3 = 2.0 F_4 = 3.0000000000000004 F_5 = 5.000000000000001 F_6 = 8.000000000000002 F_7 = 13.000000000000002 F_8 = 21.000000000000004 F_9 = 34.00000000000001 F_10 = 55.000000000000014 F_11 = 89.00000000000003
3 Algoritmo Ricorsivo
Un modo più intuitivo per calcolare \(F_n\) consiste nell'utilizzare direttamente la definizione data.

Questo algoritmo, a differenza di quello precedente, è corretto, ovvero calcola l'esatto valore di \(F_n\) per ogni \(n\). Detto questo, fib2() risulta comunque inefficiente.
3.1 Complessità
Per analizzare la complessità di questo algoritmo definiamo
\[T(n) := \text{numero di operazioni eseguite da } Fib2(n)\]
Dal codice di \(Fib2(n)\) troviamo che
\[T(n) = \begin{cases} T(n-1) + T(n-2) + O(1) \,\,&,\,\, n \geq 3 \\ O(1) \,\,&,\,\, n = 1, 2 \\ \end{cases}\]
Al fine di calcolare \(T(n)\) possiamo utilizzare la tecnica dell'albero della ricorsione, che consiste nel rappresentare l'esecuzione dell'algoritmo tramite una struttura ad albero.
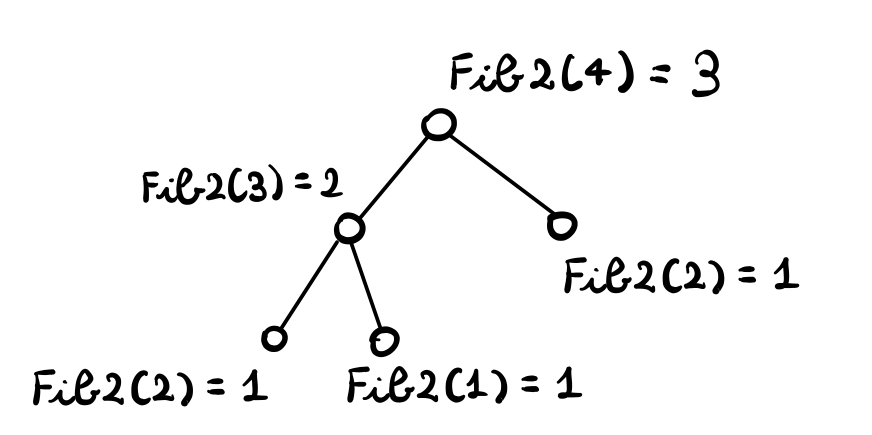
I seguenti risultati saranno necessari per stimare \(T(n)\).
3.1.1 Nodi Interni di un Albero Binario
Lemma: Il numero di nodi interni in un albero in cui ogni nodo interno ha due figli è pari al numero di foglie meno uno.
dim: Procediamo per induzione su \(n := \text{ numero di nodi dell'albero}\).
caso base (\(n = 3\)):
Graficamente abbiamo,
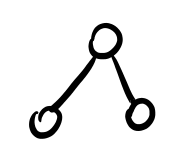
in questo caso abbiamo che il numero di nodi è pari al numero di foglie meno uno.
\[\tag*{$\checkmark$}\]
passo induttivo (\(n \geq 3\)):
Sia \(r\) la radice dell'albero. Dalle assunzioni segue che \(r\) ha due figli. Siano \(u\) e \(v\) questi figli. Graficamente abbiamo,
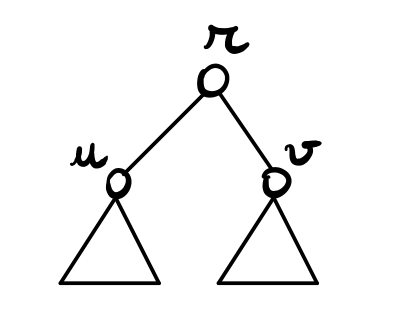
Dato che i sottoalberi radicati in \(u\) e \(v\) hanno almeno un nodo in meno dell'albero di partenza, possiamo utilizzare l'ipotesi induttiva a questi due sottoalberi per trovare
\[\begin{cases} \text{numero nodi interni a } u &= \text{numero fogli sotto u } - 1 \\ \text{numero nodi interni a } v &= \text{numero fogli sotto v } - 1 \\ \end{cases}\]
In totale quindi abbiamo
\[\begin{split} \text{# nodi interi totali} &= 1 + \text{# nodi interni a } u + \text{# nodi interni a } v \\ &= 1 + (\text{# nodi interni a } u - 1) + (\text{# nodi interni a } v - 1) \\ &= \text{# foglie sotto } r - 1 \\ \end{split}\]
\[\tag*{$\blacksquare$}\]
3.1.2 Foglie Albero di Ricorsione di \(Fib2(n)\)
Lemma: Il numero di foglie nell'albero di ricorsione di \(Fib2(n)\) è \(F_n\).
dim: Procediamo sempre per induzione su \(n\).
caso base (\(n = 1,2\)):
Per \(n=1,2\) graficamente abbiamo,
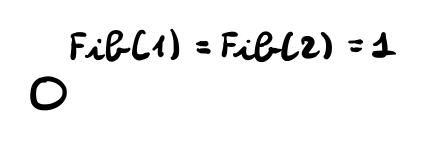
\[\tag*{$\checkmark$}\]
passo induttivo (\(n \geq 3\)):
Consideriamo l'albero di \(Fib2(n)\)
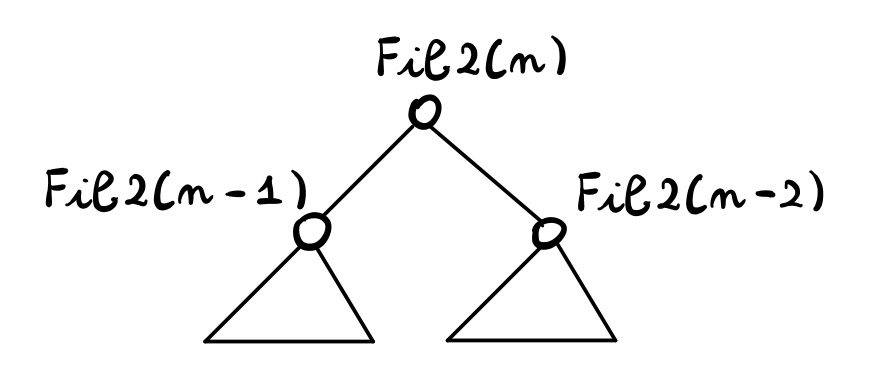
Utilizzando l'ipotesi induttiva sui due sottoalberi troviamo
\[\begin{split} \text{# foglie in } Fib2(n) &= \text{# foglie in } Fib2(n-1) + \text{# foglie in } Fib2(n-2) \\ &= F_{n-1} + F_{n-2} \\ &= F_n \end{split}\]
\[\tag*{$\blacksquare$}\]
Mettendo assieme questi risultati troviamo
\[\begin{split} T(n) &= \text{# nodi albero di } Fib2(n) \\ &= \text{# nodi interni } + \text{ # foglie } \\ &= (F_n - 1) + F_n \\ &= 2 F_n - 1 \\ \end{split}\]
e quindi
\[T(n) = \approx F_n \approx \phi^n\]
ovvero abbiamo un algoritmo esponenziale
4 Algoritmo Dinamico
Se analizziamo l'albero di ricorsione di \(Fib2(n)\) notiamo che ci sono molte computazioni ripetute, e quindi l'algoritmo fa molto lavoro superfluo.
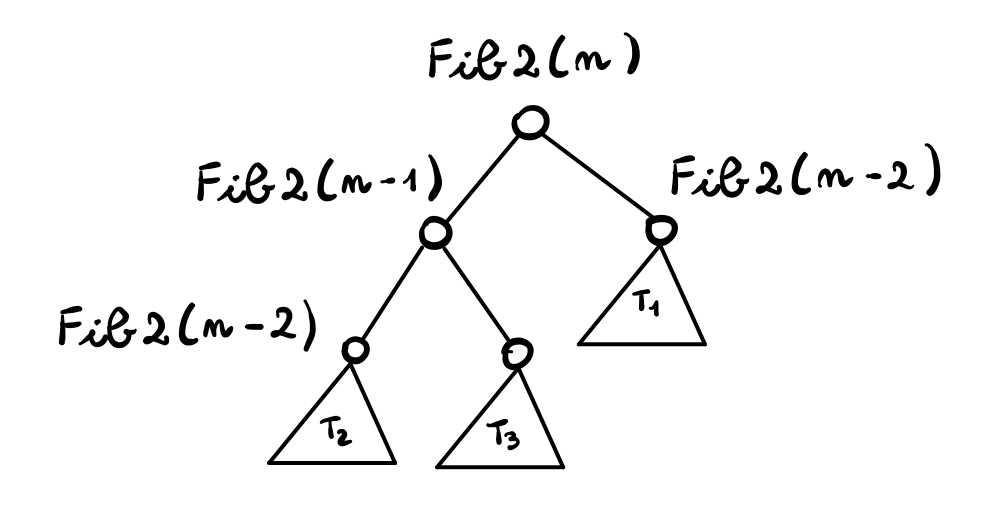
L'idea è quindi quella di memorizzare i risultati delle varie chiamate in una tabella. Così facendo non finiamo mai di calcolare due volte la stessa cosa: la prima volta la calcoliamo e la salviamo nella tabella; dalla seconda in poi al posto di calcolarla possiamo semplicemente leggerla dalla tabella.
Questa idea viene implementata nel seguente algoritmo

Questo algoritmo è sia corretto che efficiente, in quanto \(T(n) = O(n)\). Detto questo, per memorizzare i vari risultati l'algoritmo utilizza anche un \(O(n)\) di memoria.
5 Algoritmo Iterativo
L'idea in questo caso è quella di togliere il costo di \(O(n)\) sulla memoria. Per fare questo ci basta notare che per calcolare \(F_n\) abbiamo bisogno solo dei due numeri precedenti nella sequenza.
Troviamo quindi il seguente algoritmo

Questo algoritmo è corretto, ha una complessità temporale di \(O(n)\) e occupa una memoria costante di \(O(1)\) in quanto utilizza solamente \(3\) varaibili.
6 Algoritmo Lineare
L'ultimo algoritmo che vedremo si basa sulla seguente proprietà, ripresa dall'algebra lineare.
Lemma:
\[\begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix}^n = \begin{pmatrix} F_{n+1} & F_n \\ F_n & F_{n-1} \\ \end{pmatrix}\]
dim: Procdiamo per induzione su \(n\)
caso base (\(n = 1\)):
\[\begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix} = \begin{pmatrix} F_2 & F_1 \\ F_1 & F_0 \\ \end{pmatrix}\]
\[\tag*{$\checkmark$}\]
passo induttivo (\(n \geq 1\)): Utilizzando l'ipotesi induttiva e la definizione del prodotto tra matrici troviamo
\[\begin{split} \begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix}^n &= \begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix}^{n-1} \cdot \begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix} \\ &= \begin{pmatrix} F_n & F_{n-1} \\ F_{n-1} & F_{n-2} \\ \end{pmatrix}^{n-1} \cdot \begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix} \\ &= \begin{pmatrix} F_n + F_{n-1} & F_n \\ F_{n-1} + F_{n-2} & F_{n-1} \\ \end{pmatrix} \\ &= \begin{pmatrix} F_{n+1} & F_n \\ F_n & F_{n-1} \\ \end{pmatrix} \\ \end{split}\]
\[\tag*{$\blacksquare$}\]
Continuando, per calcolare in modo veloce l'\(n\) esima potenza di un numero, possiamo utilizzare il seguente approccio di tipo divide et impera
\[a^n = \begin{cases} \Big(a^{\frac{n}{2}}\Big)^2 \,\,&,\,\, n \text{ pari} \\ \Big(a^{\frac{n-1}{2}}\Big)^2 \cdot a \,\,&,\,\, n \text{ dispari} \\ \end{cases}\]
L'algoritmo finale è quindi formato da due funzioni: MatrixExp(A, k), che calcola in modo efficiente la potenza di una matrice

Fibo5(n), che calcola in modo efficiente \(F_n\)

7 Sommario
La situazione finale è quindi la seguente