ASD2 - 04 - Riduzioni I
Date:
Course Site:
Lecturer: Francesco Pasquale
Table of Contents:
In questa lezione abbiamo introdotto il concetto della riduzione polinomiale e abbiamo poi fatto vedere come è possibile utilizzare le riduzioni per risolvere i problemi.
La riduzione polinomiale è una tecnica algoritmica che può essere utilizzata per risolvere dei problemi.
In particolare una riduzione polinomiale permette di risolvere un problema \(Q\) partendo da una conoscenza pregressa che ci dice come risolvere un altro problema \(P\) e utilizzando una funzione che ci permette di passare da istanze del problema \(Q\) a istanze del problema \(P\) in un tempo polinomiale.
Lo schema da tenere a mente è dunque il seguente
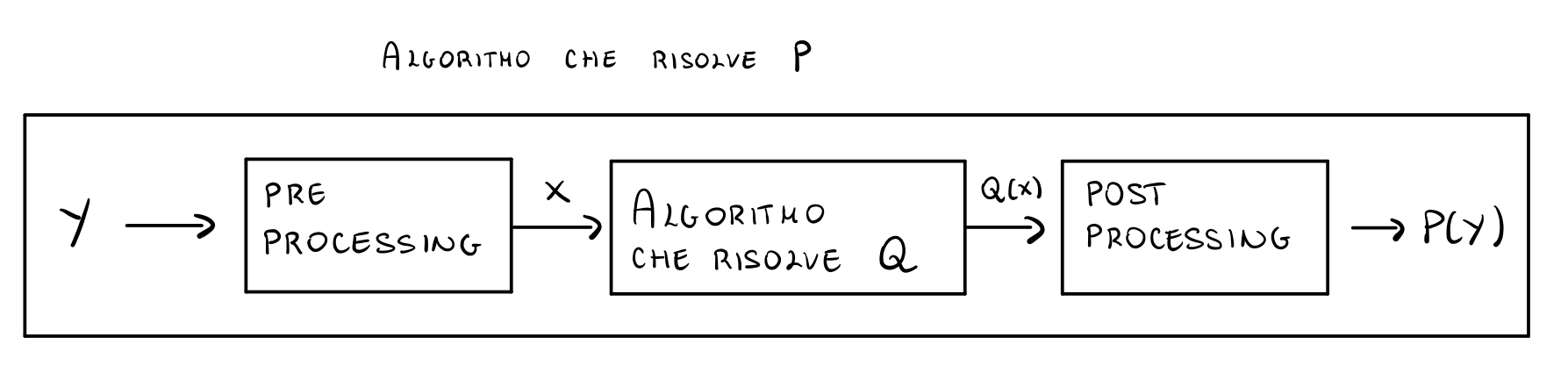
Per cercare di far capire meglio come funziona questa tecnica algoritmica andiamo a mostrare un esempio di come una riduzione polinomale può essere utilizzata per risolvere il problema \(\text{2-SAT}\).
Il problema \(\text{2-SAT}\) è il famoso problema di soddisfacibilità di una formula booleana, e può essere descritto come segue: data una formula booleana in forma \(\text{2-CNF}\), trovare una assegnazione di verità per le variabili che soddisfa la formula. Formalmente,
Input: Formula \(\phi\) in forma \(\text{2-CNF}\) (Conjunctive Normal Form), ovvero formata da un and (\(\land\)) di or (\(\lor\)) di clausole contenenti due letterali. In simboli,
\[\phi = (l_1^1 \lor l_1^2) \,\, \land \,\, (l_2^1 \lor l_2^2 ) \,\, ... \,\, (l_m^1 \lor l_m^2)\]
con \(l_j^i \in \{x_1, x_2, ..., x_n, \overline{x}_1, \overline{x}_2, ..., \overline{x}_n\}\) per \(i=1, 2\) e \(j=1, ..., m\).
Soluzione: Se \(\phi\) è soddisfacibile, assegnazione \(\tau: \{x_1, x_2, ..., x_n\} \to \{True, False\}\) che soddisfa \(\phi\). Altrimenti \(None\).
Segue qualche esempio per familiarizzare meglio con il problema.
Se \(\phi = (x_1 \lor x_2) \land (\overline{x}_1 \lor x_2) \land (x_2 \lor x_3)\), allora
\[\tau(x_1) = \tau(x_2) = \tau(x_3) = True\]
è una assegnazione che soddisfa la formula.
Se \(\phi = (\overline{x}_1 \lor x_2) \land (\overline{x}_2 \lor x_3) \land (\overline{x}_3 \lor \overline{x}_1) \land (x_1 \lor x_2) \land (\overline{x}_2 \lor x_1)\) allora non esiste una assegnazione che soddisfa \(\phi\).
La risoluzione del problema appena descritto di basa sulla riformulazione del problema all'interno della teoria dei grafi tramite una riduzione polinomiale. In particolare, data una formula \(\phi\) di \(\text{2-SAT}\), vogliamo costruire il grafo delle implicazioni \(G_{\phi}\) di \(\phi\) in modo tale da ridurre il problema di soddisfacibilità ad un problema inerente alla struttura del grafo delle implicazioni.
Andiamo adesso a discutere la struttura qualitativa del grafo delle implicazioni, per poi formalizzare il tutto:
Per ogni variabile \(x_i\) in \(\phi\), il grafo \(G_{\phi}\) contiene due nodi, uno associato a \(x_i\) e l'altro associato a \(\overline{x}_i\).
Data una clausola \((\alpha \lor \beta)\) in \(\phi\), il grafo \(G_{\phi}\) contiene sia l'arco \(\overline{\alpha} \to \beta\) che e l'arco \(\overline{\beta} \to \alpha\). Questi due archi vengono utilizzati per rappresentare il fatto che per poter soddisfare la formula \(\phi\), la presenza della clausola \((\alpha \lor \beta)\) porta al dover soddisfare le seguenti due implicazioni
\[\begin{cases} \overline{\alpha} \implies \beta \\ \overline{\beta} \implies \alpha \end{cases}\]
queste implicazioni ci dicono essenzialmente che, se andiamo ad impostare a False una variabile tra \(\alpha\) e \(\beta\), allora l'altra variabile deve necessariamente essere impostata a True per poter soddisfare l'intera formula. Dal punto di vista di un arco \((u, v)\) del grafo \(G_{\phi}\), abbiamo che se \(\tau(u) = True\), allora necessariamente \(\tau(v) = True\).
Formalmente il grafo \(G_{\phi} = (V, e)\) è costruito come segue
\(V := \{x_1, x_2, ..., x_n, \overline{x}_1, \overline{x}_2, ..., \overline{x}_n\}\), con \(x_i\) variabile di \(f\).
\(E := \{(\alpha, \beta) \in V \times V: \,\, \overline{\alpha} \lor \beta \text{ è una clausola di } \phi\}\)
Esempio: Se \(\phi = (x_1 \lor x_2) \land (\overline{x}_2 \lor x_3)\) il grafo delle implicazioni \(G_{\phi}\) è il seguente
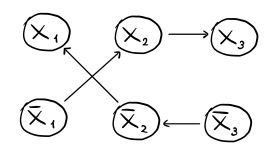
Osserviamo a questo punto che a partire dal grafo delle implicazioni \(G_{\phi}\) possiamo immediatamente capire quando la formula \(\phi\) non è soddisfacibile.
In precedenza abbiamo infatti menzionato il fatto che se \(u\) e \(v\) sono connessi tramite un arco, allora in qualsiasi assegnazione \(\tau\) che soddisfa \(\phi\) i lettarali \(u\) e \(v\) devono avere lo stesso valore di verità. Possiamo estendere per transitività questo risultato non solo ai nodi connessi tramite un arco, ma anche ai nodi connessi tramite un cammino. Ma allora, se esiste un ciclo \(\pi = \langle v_0, v_1, ..., v_k=v_0\rangle\) che contiene sia una variabile \(x_i \in \pi\) che il suo negato \(\overline{x}_i \in \pi\), abbiamo che qualsiasi assegnazione \(\tau\) non potrà mai soddisfare la formula, in quanto se \(\tau\) soddisfa \(\phi\), allora se \(\tau(x_i) = True\) si ha che \(\tau(\overline{x}_i)\) = True, in quanto \(x_i\) e \(\overline{x}_i\) sono connessi da un cammino in \(G_{\phi}\), e quindi \(\tau(x_i) = False\), il che è un assurdo. In modo analogo il caso \(\tau(x_i) = False\) porta ad un assurdo, e quindi \(\tau\) non può soddisfare \(\phi\) se esiste un tale ciclo \(\pi\).
A questo punto consideriamo il DAG formato dalle componenti fortemente connesse del grafo \(G_{\phi}\) (tale DAG esiste sempre). Se impostiamo a True un letterale in un nodo del DAG, allora dobbiamo impostare a True anche tutti gli altri letterali contenuti nello stesso nodo del DAG e i letterali contenuti in nodi puntati dal nodo preso in considerazione.
Nasce dunque la seguente strategia per trovare una assegnazione di verità: si comincia assegnando True ai letterali presenti nell'ultima componente del DAG; successivamente si cancellano i letterali a cui è già stato assegnato il valore di verità. Si ripete quindi questo procedimento andando ad ignorare i nodi del DAG che contengono la versione negata dei letterali appena trovati. Il processo termina una volta che tutti i nodi del DAG sono stati o analizzati o ignorati.
Per cercare di capire l'assegnazione di verità che andiamo a costruire consideriamo il seguente grafo
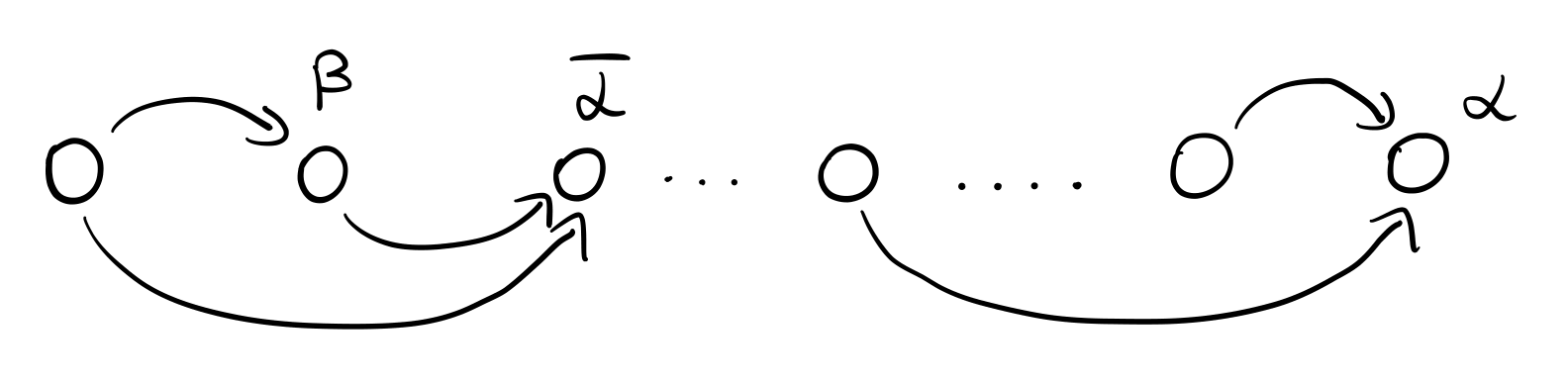
assegnando al letterale \(\alpha\) il valore True, ne segue che \(\tau (\overline{\alpha}) = False\). Ma allora, per essere sicuri che l'assegnazione che sto creando soddisfi la formula \(\phi\), bisogna assicurarsi che non può esistere un \(\beta\) tale che \((\beta, \overline{\alpha}) \in E\) con \(\tau(\beta) = True\). Infatti per costruzione sappiamo che
\[\begin{split} (\beta, \overline{\alpha}) \in E &\implies (\overline{\beta} \lor \overline{\alpha}) \text{ è una clausola di } \phi \\ &\implies (\alpha, \overline{\beta}) \in E \\ &\implies \overline{\beta} \text{ fa parte dell'ultimo nodo del DAG} \\ &\implies \tau(\overline{\beta}) = True \\ &\implies \tau(\beta) = False \\ \end{split}\]
Segue una descrizione dettagliata dell'algoritmo.

La complessità dell'algoritmo è \(\theta(n + m)\), dove \(n\) è il numero di variabili e \(m\) il numero di clausole. Infine, nel seguente link è disponibile una implementazione in python dell'algoritmo appena descritto 2sat.py.