ASD2 - 07 - Ricerca Esaustiva Intelligente
Date:
Course Site:
Lecturer: Francesco Pasquale
Table of Contents:
In questa lezione abbiamo iniziato ad introdurre delle tecniche che ci permettono di gestire i problemi NP-hard, ovvero i problemi per cui non si conosce nessun algoritmo polinomiale. La prima tecnica introdotto è quella della ricerca esaustiva intelligente.
La ricerca esaustiva intelligente è un approccio alla risoluzione di problemi N-completi, e consiste nel fare delle ricerche che cercano di filtrare il più possibile lo spazio delle possibili soluzioni.
Da un punto di vista teorico, per quanto riguarda il worst-case di questi algoritmi abbiamo che il costo computazionale è comunque esponenziale. Detto questo questi algoritmi, se sono buoni, riescono ad ottenere dei buoni risultati sulla maggior parte delle istanze.
Esistono due tecniche principali per effettuare una ricerca esaustiva intelligente. Queste sono:
Backtracking: Tecnica utilizzata per problemi decisionali.
Branch and Bound: Tecnica utilizzata per problemi di ottimizzazione.
L'idea che si trova alla base del backtracking è che molte volte è possibile rigettare una soluzione semplicemente guardando solo una piccola parte di essa. Con questo approccio è quindi possibile esplorare l'insieme delle soluzioni un passo alla volta, eliminando possibili soluzioni non appena si verifica una situazione non valida.
Per chiarire meglio le idee, consideriamo una formula \(\varphi\) del problema \(\text{SAT}\). Se la formula \(\varphi\) contiene la clausola \((x_1 \lor x_2)\), allora tutte le possibili soluzioni in cui \(x_1 = x_2 = \text{False}\) possono essere scartate.
Notiamo che questo tipo di ricerca esaustiva può essere rappresentata da un albero
dove \(\varphi'\) rappresenta la formula \(\varphi\) in cui \(w\) viene impostato a \(0\), mentre \(\varphi''\) rappresenta la formula \(\varphi\) in cui \(w\) viene impostato a \(1\).
Presentiamo adesso un esempio completo di backtracking per il problema di soddisfacibilità \(\text{SAT}\).
Consideriamo come formula iniziale \(\varphi\) la seguente
\[(w \lor x \lor y \lor z) \land (w \lor \overline{x}) \land (x \lor \overline{y}) \land (y \lor \overline{z}) \land (z \lor \overline{w}) \land (\overline{w} \lor \overline{z})\]
Possiamo rappresentare l'esecuzione di una ricerca esaustiva intelligente tramite il backtracking con il seguente albero
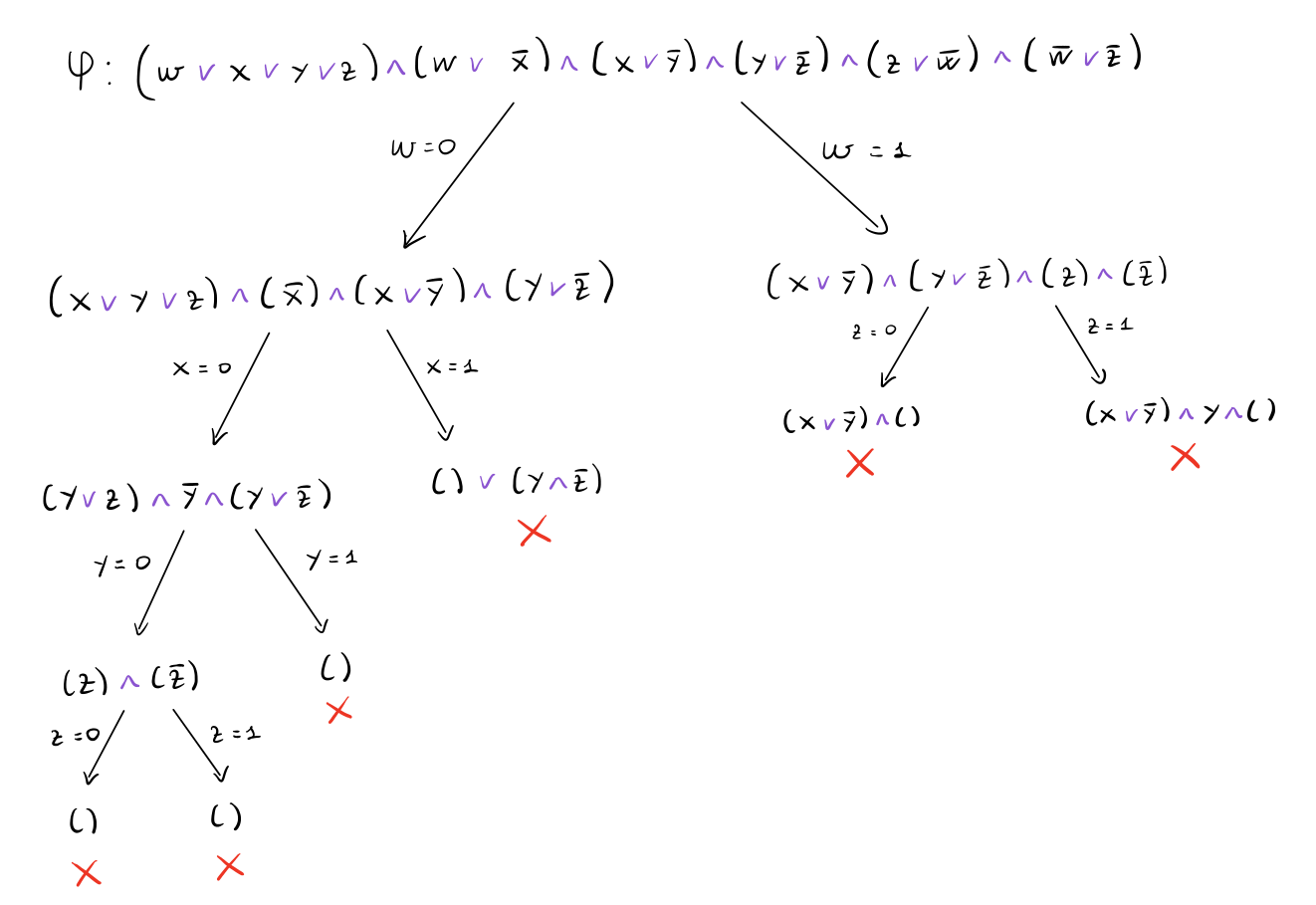
Dato che alla fine tutti i rami hanno portato a formule insoddisfabili, possiamo concludere che la formula \(\varphi\) iniziale non è soddisfacibile. Notiamo inoltre che per scoprirlo non abbiamo dovuto controllare tutte le \(2^4 = 16\) assegnazioni di verità, ma solo \(10\).
Osservazione: Dato che il beneficio del backtracking deriva dal "tagliare" parti dello spazio di ricerca, è molto utile, per problemi come il \(\text{SAT}\), scegliere le variabili con cui espandersi all'interno della clausola con il più piccolo numero di letterali.
Il branch and bound è l'analogo del backtracking ma per problemi di ottimizzazione.
Per poter implementare un algoritmo di branch and bound dobbiamo essere in grado di risolvere i seguenti due problemi:
Dobbiamo gestire il fatto di avere solo delle soluzioni parziali a disposizione. In altre parole dobbiamo capire qual'è il modo migliore per completare uan soluzione parziale.
Dobbiamo trovare un criterio che ci permetta di sapere quando eliminare delle soluzioni parziali, dopo averle completate. Quando dobbiamo eliminare una soluzione parziale infatti, al posto di calcolare il costo esatto della soluzione, che sarebbe inefficiente, possiamo utilizzare un quick lower bound per essere sicuri che il costo della soluzione parziali superi quello di una soluzione che abbiamo già incontrato.
Segue uno pseudocodice che implementa questa idea
