ADRC - 01 - Modello Distribuito

Le entità \(x \in \xi\) si comportano in modo reattivo, nel senso che ogni entità risponde solamente se sottoposta a eventi esterni. Ci sono tre tipologie di eventi esterni, tra cui troviamo:

• Ricezione di un messaggio.

• Sveglia dell'alarm clock.

• Impulsi spontanei.

Mentre le prime due tipologie di eventi esterni sono esterni rispetto all'entità, ma sono comunque generati all'interno del sistema distribuito, la terza tipologia di eventi esterni, gli impulsi spontanei, sono eventi che vengono generati al di fuori del sistema e che sono utilizzati per far partire la computazione distribuita.

---

Quando una entità \(x \in \xi\) riceve un evento \(e\), l'entità \(x\) esegue una serie di operazioni che prende il nome di action (azione). Una action, per poter essere definita tale, deve rispettare le seguenti proprietà:

• Deve essere finita, ovvero deve contenere un numero finito di operazioni;

• Deve essere indivisibile, ovvero le operazioni contenute nella action devono essere eseguite una dopo l'altra, senza interruzioni;

• Deve essere terminante, ovvero una volta iniziata deve terminare in un tempo finito.

La particolare azione che viene eseguita dipende dai seguenti due fattori

1. Il tipo di evento \(e\);

2. Lo stato in cui si trovata l'entità nell'istante in cui si riceve l'evento \(e\).

Per descrivere questa associazione si utilizzano quindi delle regole della forma

\[\text{ Status } \times \text{ Event } \rightarrow \text{ Action }\]

---

Il comportamento di una entità \(x \in \xi\) è definito come l'insieme di tutte le regole applicate al nodo \(x\), e viene indicato con il simbolo \(B(x)\). Tale comportamento deve essere completo e non-ambiguo, ovvero per ogni coppia \((s, e)\) con \(s\) stato ed \(e\) evento, si deve avere che

\[|\{ r \in B(x): \,\, r \text{ è attivata da } (s, e) \}| = 1\]

ovvero ci deve essere una e una sola regola \(r\) attivata dalla coppia \((s, e)\). L'insieme \(B(x)\) è anche chiamato il protocollo di x.

Il comportamento collettivo di una collezione di entità \(\xi\) è l'insieme

\[B(\xi) := \{B(x) : \,\, x \in \xi\}\]

Tale insieme definisce il nostro protocollo (o algoritmo) distribuito. Esistono varie tipologie di comportamenti collettivi, tra cui troviamo anche il seguente

Definizione: Un protocollo distribuito \(B(\xi)\) è detto omogeneo se e solo se

\[\forall x, y \in \xi: \,\, B(x) = B(y)\]

Ogni protocollo distribuito può essere trasformato in un protocollo distribuito omogeneo andando ad introdurre una variabile nella memoria di ogni nodo che specifica il particolare ruolo del nodo e modificando le azioni da eseguire in modo da tenere conto del ruolo.

Le entità comunicano tra loro inviandosi dei messaggi, che sono sequenze finite di bits. Per ogni nodo \(x \in \xi\) definiamo

• \(N_{out}(x) :=\) L'insieme delle entità a cui \(x\) può inviare un messaggio in modo diretto.

• \(N_{in}(x) :=\) L'insieme delle entità che possono inviare un messaggio diretto ad \(x\).

Questa relazione di "vicinato" definisce un grafo diretto \(\overrightarrow{G} = (V, \overrightarrow{E})\), dove \(V\) è l'insieme dei nodi, ciascuno dei quali rappresenta una entità in \(\xi\), ed esiste l'arco \((x, y)\) sse \(x\) può inviare un messaggio all'entità \(y\), ovvero sse \(x \in N_{in}(y)\).

Il grafo \(\overrightarrow{G}\) descrive la topologia di comunicazione del nostro ambiente di lavoro. Rispetto al grafo \(\overrightarrow{G}\) troviamo le seguenti notazioni utili da ricordare

• \(n(\overrightarrow{G}) := \text{ numero di vertici.}\)

• \(m(\overrightarrow{G}) := \text{ numero di archi.}\)

• \(d(\overrightarrow{G}) := \text{ diametro del grafo.}\)

Il modello distribuito classico con comunicazione point-to-point utilizza i seguenti assiomi di base:

• Finite Communication Delay

  In assenza di failures i ritardi di comunicazione sono finiti.

• Local Orientation

  Ogni entità è in grado di identificare e distinguere ciascun vicino, sia entrante che uscente. Questa identificazione avviene tramite l'utilizzo di una funzione local al nodo \(\lambda_x(\cdot)\) che associa a ciascun arco incidente al nodo un particolare numero di porta.

  \[\lambda_x(x, y) := \text{ etichetta associata dal nodo } x \text{ all'arco } (x, y)\]

  La funzione \(\lambda_x(\cdot)\) deve essere iniettiva in modo da permettere al nodo di identificare univocamente ogni vicino. Osserviamo poi come due entità diverse possono assegnare due etichette diverse allo stesso arco. In formula

  \[\underbrace{\lambda_x(x, y)}_{\text{ locale a } x} \neq \underbrace{\lambda_y(x, y)}_{\text{locale a } y}\]

  questo significa che ogni arco del grafo ha esattamente due etichette.

  

---

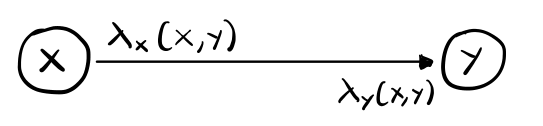
Oltre a questi assiomi base, il modello può essere caratterizzato da altri tipi di assunzioni che prendono il nome di restrizioni. Notiamo che ogni tipo di assunzione extra che utilizzamo in un protocollo limita (o restringe) l'applicabilità del procollo stesso. Bisogna quindi essere molto cauti nell'utilizzo di queste restrizioni.

La complessità di un protocollo distribuito può essere descritta rispetto alle seguenti tre quantità di interesse

Al fine di poter definire lo stato globale del nosto ambiente distribuito iniziamo descrivendo le condizioni iniziali del sistema.

Sia \(x \in \xi\) una entità. Indichiamo con il simbolo \(\sigma(x, 0)\) lo stato iniziale interno dell'entità \(x\). Tale stato contiene al suo interno i seguenti elementi

• Il contenuto iniziale di tutti i registri di \(x\).

• Il valore iniziale del local alarm clock \(C_x\) di \(x\).

Una descrizione statica del sistema prima dell'esecuzione del protocollo distribuito è quindi la seguente

\[\Sigma(0) := \{ \sigma(x, 0): \,\,\, x \in \xi\}\]

---

Ricordiamo che nel modello che stiamo descrivendo ci sono tre tipologie di eventi, che sono

• Spontaneous impulses (spontaneously).

• Reception of a message (receiving).

• Alarm clock ring (when).

L'esecuzione di una azione può potenzialmente generare nuovi eventi. Ad esempio l'operazione send() genera un nuovo evento di tipo receiving, mentre l'operazione set_alarm() genera un evento di tipo when. Anche se gli eventi vengono generati, questo non implica necessariamente che verranno verificati durante l'esecuzione del protocollo. A seconda delle dinamiche della particolare esecuzione infatti potrebbero accadere varie cose, tra cui il fallimento di determinati nodi e archi, che potrebbe portare un evento generato a non verificarsi. Inoltre, anche nel caso in cui un evento generato finisce per verificarsi, non lo fa nel momento in cui viene generato, ma solo in un tempo successivo. Alcune volte il delay tra quando l'evento viene generato e quando si verifica è noto, mentre altre volte non lo è. Questo significa che diversi delay danno forma a diverse esecuzioni dello stesso protocollo, che possono quindi portare a diversi outcomes. In ogni caso la correttezza di un protocollo non deve dipendere dal particolare ordine in cui gli eventi si verificano.

Indichiamo con \(t(e)\) il tempo di generazione dell'evento \(e\). Tutti gli spontenous impulses vengono generati al tempo \(t = 0\), in quanto sono proprio gli eventi che fanno partire l'esecuzione del protocollo. L'insieme che contiene questi eventi è detto set of initial events.

Nel nostro modello il tempo è visto dagli occhi di un osservatore esterno al sistema. Dato un istante di tempo \(t\) è possibile separare l'asse del tempo nelle seguenti \(3\) parti

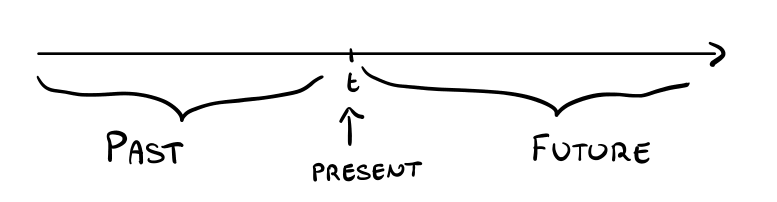
Indichiamo con \(Future(t)\) l'insieme degli eventi futuri che sono stati generati al tempo \(\leq t\) e che ancora devono verificarsi.

---

Prendendo in considerazione il tempo \(t\) indichiamo con \(\sigma(x, t)\) lo stato interno dell'entità \(x\) al tempo \(t\). Seguono due proprietà importanti relative agli stati interni delle entità

Proprietà 1: Supponiamo che uno stesso evento accada al nodo \(x\) al tempo \(t\) in due esecuzioni diverse, e indichiamo \(\sigma_1, \sigma_2\) gli stati interni di \(x\) nelle due esecuzioni. Se \(\sigma_1 = \sigma_2\) allora il nuovo stato interno di \(x\) sarà lo stesso in entrambe le esecuzioni.

Proprietà 2: Supponiamo che uno stesso evento accada al nodo \(x\) e al nodo \(y\) al tempo \(t\) nella stessa esecuzione, e siano \(\sigma_x, \sigma_y\) gli stati interni di \(x\) e \(y\). Se \(\sigma_x = \sigma_y\) allora il nuovo stato interno di \(x\) sarà lo stesso del nuovo stato interno di \(y\).

---

Siamo adesso in grado di descrivere lo stato globale del nostro sistema al tempo \(t\). Infatti, una descrizione statica del nostro sistema al tempo \(t\) è data da

\[\Sigma(t) := \{\sigma(x, t): \,\, x \in \xi\}\]

notiamo però che la particolare esecuzione potrebbe aver generato degli eventi che ancora devono verificarsi. Per descrivere in modo completo lo stato globale al tempo \(t\) necessitiamo quindi le seguenti cose

\[C(t) := \Big(\Sigma(t), Future(t) \Big)\]

La configurazione iniziale \(C(0)\) oltre a contenere l'insieme degli stati iniziali \(\Sigma(0)\) contiene anche l'insieme degli eventi spontanei, rappresentato da \(Future(0)\). Ambienti che differiscono solamente nella loro configurazione iniziale \(C(0)\) sono chiamati istanze dello stesso sistema.

Un problema \(P\) per il nostro modello distribuito è definito come una tripla

\[P = \langle P_{init}, P_{final}, R \rangle\]

in cui,

• \(P_{init}\) è un predicato che vincola i valori dei registri delle entità all'inizio della computazione.

• \(P_{final}\) è un predicato che vincola i valori dei registri delle entità alla fine della computazione.

• \(R\) è un insieme di restrizioni.

---

Un protocollo \(B\) che risolve il problema \(P\) deve specificare come le entità possono passare dal soddisfare la condizione \(P_{init}\) al soddisfare la condizione \(P_{final}\) sotto i vincoli imposti da \(R\).

Un passo importante nella definizione di un protocollo distribuito è la definizione dei possibili stati in cui le entità del modello si possono trovare. Tra le varie tipologie di stati troviamo i seguenti di particolare interesse

• \(S_{init}\) := Stati utilizzati all'inizio dell'esecuzione del protocollo.

• \(S_{term}\) := Stati che una volta raggiunti non possono essere cambiati dal protocollo.

• \(S_{start}\) := Stati in \(S_{init}\) che fanno partire l'esecuzione del protocollo.

• \(S_{final}\) := Stati in \(S_{term}\) in cui non c'è bisogno di effettuare alcuna attività.

Notiamo che

\[S_{final} \subseteq S_{term} \,\,\,\,,\,\,\,\, S_{start} \subseteq S_{init}\]

---

Diciamo che un protocollo \(B\) termina se, per ogni configurazione iniziale \(C(0)\) che soddisfa \(P_{init}\) e per ogni esecuzione che parte dallo stato iniziale \(C(0)\), il predicato

\[\text{Terminate}(t) \equiv \Big(\{status_t \subseteq S_{term}\}\Big) \land \Big( Future(t) = \emptyset\Big)\]

vale per qualche valore di \(t\).

Si parla invece di terminazione esplicita quando tutti i nodi sono consapevoli del fatto che il protocollo è terminato. Questa situazione è verificata quando

\[\text{Explicit_Terminate}(t) \equiv \Big( \{status_t\} \subseteq S_{final} \Big)\]

è verificato per qualche \(t\).

---

Infine, diciamo che il protocollo \(B\) è corretto se per tutte le configurazioni che partono da una configurazione iniziale che soddisfa \(P_{init}\), si ha che

\[\exists t > 0: \,\, \forall t' > t: P_{final}(t)\]