ADRC - 05 - Spanning Tree Construction

1 Lecture Info

Data: [2018-10-25 gio]

Capitolo del libro: 2 - Basic Problems and Protocols

In questa lezione abbiamo trattato il problema di della costruzione distribuita di uno spanning tree di una data rete, introducendo due protocolli per risolvere il problema e andandone ad analizzare la correttezza e la complessità. Per terminare la lezione sono state presentate alcune osservazioni fondamentali relative al problema analizzato.

2 ST Construction Problem

Lo Spanning Tree Construction problem consiste nel costruito in modo distribuito un qualsiasi spanning tree $T$ (e non il minimo), data una rete $G$.

Il problema è formalizzato dalla tripla $P = \langle P_{init}, P_{final}, R \rangle$ dove,

$P_{init}(t) = \forall x \in V: \,\,\, \text{Tree-Neigh}(x) = \{\}$

$P_{final}(t) = \bigcup\limits_{x \in V} \text{Tree-Neigh}(x)$ forma uno spanning tree della rete $G=(V,E)$.

$R = \begin{cases} \text{Total Reliability (TR)} \\ \text{Bidirectional Link (BL)} \\ \text{Connectivity (CN)} \\ \text{Unique Initiator (UI)} \\ \end{cases}$

A differenza di algoritmi centralizzati come l'algoritmo di Kruskal per la costruzione del minimo spanning tree, nel nuovo mondo distribuito la conoscenza dello spanning tree $T$ che viene costruito è divisa nei vari nodi della rete. Ogni nodo quindi conosce solamente la parte locale di $T$ a lui adiacente, e non esiste nessun nodo che ha una visione globale dello spanning tree costruito.

3 Protocollo SHOUT

Come oramai ci stiamo abituando, per risolvere questo problema dobbiamo definire un protocollo che, tramite l'invio di particolari messaggi, riesce a costruire uno spanning tree della rete. Per quanto riguarda i messaggi, siamo interessati alle seguenti due tipologie di messaggi che ogni nodo può inviare:

Un messaggio per chiedere ad un nodo adiacente se vuole far parte dell'albero che si sta costruendo. (Messaggio $Q$)
Un messaggio per accettare di essere aggiunto all'albero che si sta costruendo. (Messaggio $Y$)
Un messaggio per rifiutare di essere aggiunto all'albero che si sta costruendo. (Messaggio $N$)

L'idea chiave per definire il nostro primo protocollo è quella di utilizzare il fatto di avere un unico initiator, assieme al fatto che in un albero esiste la relazione $\text{padre-figlio}$, e che tale relazione è monotona, ovvero un figlio ha solo un padre. Un possibile protocollo può quindi procedere con la costruzione di uno spanning tree partendo dalla sorgente (l'unico initiator), e aggiungendo di volta in volta all'albero solamente i nodi che non hanno ancora scelto il proprio padre. Questa idea è formalizzata nel seguente protocollo, che prende il nome di protocollo SHOUT.

Per quanto riguarda gli stati abbiamo $4$ possibili stati,

$S = \{\text{initiator}, \text{idle}, \text{active}, \text{done}\}$
$S_{init} = \{\text{initiator}, \text{idle}\}$
$S_{term} = \{\text{done}\}$

L'idea è che inizialmente tutti i nodi tranne uno si trovano nello stato $\text{idle}$. L'unico nodo che si trova nello stato $\text{initiator}$ si sveglia da un impulso esterno al sistema e comincia ad inviare il messaggio $Q$ di domanda a tutti i suoi vicini. Con questo messaggio il nodo sta proponendo ai nodi a lui adiecenti se vogliono essere connessi a lui all'interno dello spanning tree. Quando un nodo nello stato $\text{idle}$ riceve un messaggio $Q$, si attiva, e sceglie come padre il primo nodo da cui ha ricevuto tale messaggio. Successivamente invia il messaggio $Q$ lui stesso a tutti i nodi a lui adiacenti (tranne il nodo che l'ha attivato), e si mette nello stato $\text{active}$. Quando un nodo si trova nello stato $\text{active}$, vuol dire che ha già scelto un padre, e dunque risponderà sempre di no a tutti i messaggi di tipo $Q$ che riceve dagli altri nodi. Se invece riceve un messaggio di tipo $Y$, ovvero se è stato scelto come padre da un nodo a lui adiecente, allora aggiunge tale nodo nella sua visione locale dello spanning tree, e aumenta il contatore per indicare che quel nodo gli ha dato una risposta. Se riceve un messaggio di tipo $N$ invece aumenta solo il contatore. Una volta che il contatore diventa pari al grado del nodo, il nodo termina e va nello stato $\text{done}$.

Volendo formalizzare quanto descritto, troviamo il seguente protocollo

Lo stato $\text{done}$ è stato omesso in quanto è uno stato finale in cui il nodo non fa nulla. Andiamo adesso ad argomentare la correttezza e la complessità del protocollo SHOUT.

3.1 Correttezza

Come prima cosa argomentiamo che il protocollo termina. A tale fine sia $x$ un nodo qualsiasi, e facciamo vedere che esiste un tempo $t$ in cui il nodo $x$ passa allo stato $\text{done}$. Abbiamo due possibili casi:

Se $x$ è il nodo initiator, allora invierà a tutti i nodi adiacenti il messaggio $Q$, risvegliandoli, e dopo un po' di tempo riceverà da tutti i suoi vicini un messaggio (di tipo $Y$ o $N$), andando infine nello stato $\text{done}$.
Se $x$ è un qualsiasi altro nodo, allora, dato che $G$ è connesso, esisterà sempre un cammino che va dal nodo initiator $s$ al nodo $x$. Ma allora dopo un po' di tempo ad $x$ arriverà il messaggio $Q$.

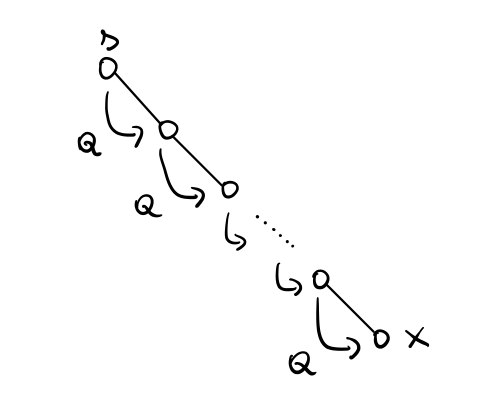
Questo fatto può essere formalmente dimostrato per induzione sulla distanza dalla sorgente il fatto che ogni nodo riceve in un tempo finito un messaggio di tipo $Q$.

Appena un nodo riceve $Q$, il nodo si sveglia, passa allo stato $\text{active}$, e invia $Q$ a tutti i nodi a lui adiacenti. Appena riceve la risposta di tutti il nodo va nello stato $\text{done}$ e termina.

Dimostriamo ora che gli archi selezionati dal protocollo formano un sottografo aciclico e connesso. A tale fine sia $x$ il nodo initiator, e sia $y \in V \setminus \{x\}$ un qualsiasi altro nodo. Vogliamo far vedere che esiste un solo cammino che collega $x$ a $y$. Spezziamo quindi la dimostrazione in due passi

Esiste almeno un cammino:

Come prima cosa mostriamo che esiste almeno un cammino che collega $x$ a $y$. Consideriamo quindi il nodo $z$ che ha fatto svegliare $y$, o, detto altrimenti, il nodo a cui $y$ ha inviato il messaggio $Y$. Per costruzione, l'arco $(z, y)$ fa parte dello spanning tree $T$. Continuando indietro così è possibile trovare un cammino da $x$ a $y$ utilizzando solo gli archi dello spanning tree costruito.
Esiste un solo cammino:

Supponiamo adesso che esistano almeno due cammini che collegano $x$ a $y$. Troviamo quindi la seguente situazione

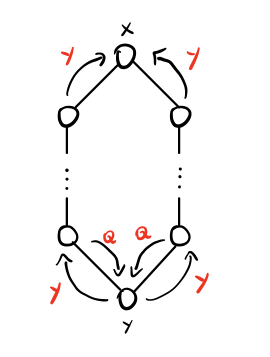
Andando ad analizzare la struttura del ciclo in funzione dei messaggi $Y$ inviati notiamo che un ciclo si può formare solo nel caso in cui un nodo invia più di un messaggio $Y$. Ma questo non è previsto dal protocollo. Troviamo quindi un assurdo e concludiamo che può esistere un solo cammino che collega $x$ a $y$.

\[\tag*{$\Huge\unicode{x21af}$}\]

3.2 Complessità

Andiamo adesso a discutere la message complexity del protocollo SHOUT. Notiamo che i messaggi inviati dal protocollo possono essere divisi in due categorie: abbiamo il messaggio $Q$ che viene inviato per effettuare una domanda, e i messaggi $Y$ a $N$ che vengono inviati in risposta al messaggio $Q$.

Andando ad effettuare una analisi per arco troviamo la seguente situazione:

Per ogni arco che andrà poi a far parte dello spanning tree costruito abbiamo che passano due messaggi: da un lato passa il messaggio di richiesta $Q$, e dall'altro passa la rispost affermativa $Y$.

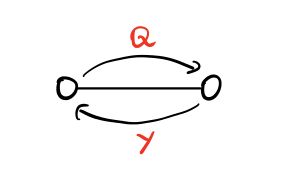
Dato che questi archi sono $n-1$, troviamo già $n-1$ messaggi di tipo $Q$ e $n-1$ messaggi di tipo $Y$.

Per i restanti archi, quelli che non fanno parte dello spanning tree, abbiamo che a due messaggi $Q$ seguono due messaggi $N$.

Questi archi poi sono $m - (n-1)$.

Andando a sommare il numero totale delle varie tipologie di messaggio troviamo

Totale Messaggi $\text{Q}$:

\[\begin{cases} 1 \text{ per archi dello spanning tree} \\ 2 \text{ per altri archi} \\ \end{cases} \implies n-1 + 2 \cdot \big(m - (n-1)\big) = 2m - n + 1\]
Totale Messaggi $\text{Y}$:

\[ 1 \text{ per archi dello spanning tree} \implies n - 1\]
Totale Messaggi $\text{N}$:

\[ 2 \text{ per altri archi} \implies 2 \cdot \big(m - (n-1)\big)\]

Infine, mettendo tutto assieme

\[\begin{split} M(\text{SHOUT}) &= \Big(2m - n + 1\Big) + \Big(2 \big(m - (n-1)\big)\Big) + \Big(n-1\Big) \\ &= 2m -n +1 +2m -2n +2 +n -1 \\ &= 4m -2n + 2 \end{split}\]

dunque abbiamo appena dimostrato che la message complexity del protocollo SHOUT è data da

\[M(\text{SHOUT}) = 4m -2n + 2\]

Osservazione: Notiamo che il protocollo SHOUT effettua un flooding di messaggi $Q$ seguiti da una reply che può essere $Y$ o $N$, a seconda se l'arco è inserito nello spanning tree oppure no. Da questo segue che $M(\text{SHOUT}) = 2 \cdot M(\text{FLOOD})$, il che torna con quanto appena dimostrato.

Per quanto riguarda l'ideal time complexity troviamo sempre un valore pari al diametro del grafo $G$ nel caso peggiore.

4 Protocollo SHOUT+

Se andiamo ad analizzare in modo più dettagliato il protocollo SHOUT è possibile notare che i messaggi $N$ non sono necessari per far sapere al nodo quando terminare. Vale infatti la seguente osservazione: se $y$ invia $N$ a $x$, allora $h$ ha anche inviato $Q$ a $x$ prima. Ma allora, se un nodo riceve il messaggio $Q$ da una porta, il nodo può semplicemente interpretare tale messaggio come il messaggio $N$, nel senso che quel nodo ha già scelto un padre.

Questa idea viene implementata nel seguente protocollo, che prende il nome di protocollo SHOUT+

Notiamo come a differenza del protocollo SHOUT, nel protocollo SHOUT+ non ci sono più i messaggi $N$. In ogni caso il comportamento è analogo a quello analizzato prima, in quanto il messaggio $Q$ contiene tutte le informazioni che portava il messaggio $N$.

4.1 Complessità

Avendo eliminato la tipologia di messaggi $N$, ci aspettiamo un calo nel numero di messaggi inviati. Andando ad effettuare una analisi per arco otteniamo infatti

Per ogni arco dello spanning tree, abbiamo la situazione di prima in cui vengono scambiati esattamente due messaggi: un messaggio $Q$ e un messaggio $Y$.
Per ogni arco che non fa parte dello spanning tree, vengono scambiati due messaggi di tipo $Q$.

Mettendo tutto assieme otteniamo una message complexity di

\[M(\text{SHOUT+}) = 2 \cdot (n-1) + 2 \cdot \big(m - (n-1) \big) = 2 \cdot m\]

4.2 Terminazione Globale nello SHOUT+

Notiamo che per come abbiamo definito lo SHOUT e lo SHOUT+, il tipo di terminazione che otteniamo è una terminazione locale, nel senso che ogni nodo sa quando il suo compito è finito, ma nessun nodo è in grado di stabilire quand'è che l'intero spanning tree è stato costruito. Detto questo, tramite una piccola modifica al protocollo è possibile ottenere una terminazione globale, in cui ogni nodo sa esattamente quando il protocollo è terminato e quando lo spanning tree è stato costruito.

L'idea è quella di far partire una operazione di accumulation a partire dalle foglie, che si sparge in alto nell'albero per arrivare infine alla radice. Per fare questo si aggiunge un nuovo messaggio al protocollo, il messaggio $\text{saturated}$. Questo messaggio viene condiviso nel seguente modo:

I nodi foglia inviano il messaggio $\text{saturated}$ al proprio padre;
Un nodo non foglia invia al proprio padre il messagio $\text{saturated}$ solo dopo averlo ricevuto da tutti i propri figli.

Graficamente otteniamo,

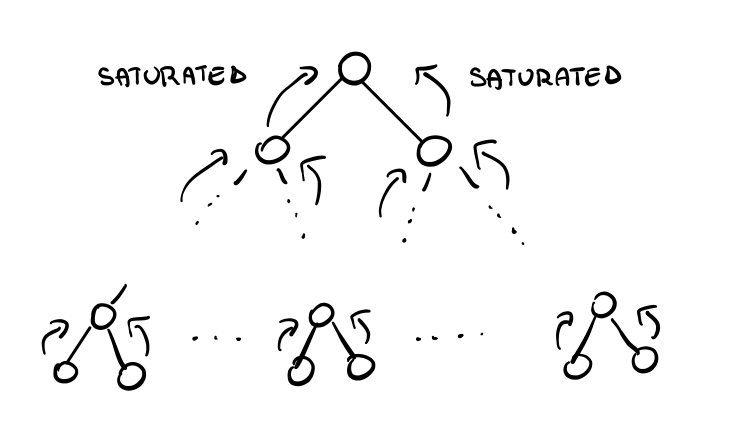
Quando la radice riceve il messaggio $\text{saturated}$ da ogni figlio, allora la radice sa che l'albero è stato costruito e può iniziare una operazione di broadcasting per indicare a tutti i nodi che l'albero è stato finalizzato.

Il costo totale per questo processo è quindi dato da $n-1$ se si vuole informare solo la radice della costruzione dell'albero, e da $2(n-1)$ se si vuole informare ogni nodo.

5 Osservazioni Finali

Segue qualche osservazione finale sulla costruzione distribuita dello spanning tree che abbiamo appena trattato.

5.1 ST tramite Broadcast

Notiamo che un qualunque protocollo di broadcast induce in modo implicito uno spanning tree della rete. In particolare lo spanning tree indotto è ottenuto definendo la relazione padre-figlio nel seguente modo

\[\text{Father}(x) := \text{nodo che manda per primo l'informazione } I \text{ al nodo } x\]

Notiamo però che questo non basta a risolvere il problema della costruzione distribuita di uno spanning tree, in quanto così facendo i nodi conoscono solo chi è il proprio padre, e non chi sono i propri figli. Questo è una conseguenza del fatto che utilizzando il broadcast non ci sono messaggi di feedback.

5.2 Lower Bound per la ST Construction

Da quanto appena notato, e dal fatto che un lower bound per il problema del broadcast è $\Omega(m)$, segue che $\Omega(m)$ è un lower bound anche per il problema della costruzione distribuita di uno spanning tree.

5.3 Che tipo di ST Costruiamo?

Notiamo che fissato un protocolo $P$ che risolve il problema della costruzione distribuita di uno spanning tree abbiamo che il particolare spanning tree distribuito dipende

Dal protocollo $P$.
Dalla particolare esecuzione del protocollo $P$, ovvero dal particolare delay dei messaggi.

Ad esempio il protocollo $\text{SHOUT+}$ è in grado di generare ogni possibile spanning tree del grafo $G$ semplicemente cambiando i ritardi dei messaggi. Una conseguenza di questo fatto è che alcune proprietà del grafo $G$ potrebbero essere perse nel particolare spanning tree costruito. Ad esempio si potrebbe avere che

\[diam(\text{ST}) \gg diam(G)\]

il che non è proprio una bella notizia.

Se invece lavoriamo in un modello sincrono allora è possibile simulare una BFS (Bredth First Search) per costruire uno spanning tree che rispetta le distanze relative.

Osservazione: Esiste una teoria, chiamata teoria degli spanners, il cui oggetto di studio è la costruzione di sottografi ricoprenti e sparsi che soddisfano determinate proprietà.

Sotto ipotesi generali dato un grafo è possibile trovare un sottografo le cui distanze relative sono peggiorate di un fattore costante $c$. Tale sottografo è chiamato spanner, mentre il fatto $c$ è chiamato stretch factor.

5.4 ST Construction con più Intiators

Poniamo ora il seguente quesito: è possibile definire un protocollo che costruisce uno spanning tree anche quando ci sono più initiators?

Esempio: nel caso del protocollo $\text{SHOUT+}$ questo non è possibile, come mostra la seguente esecuzione

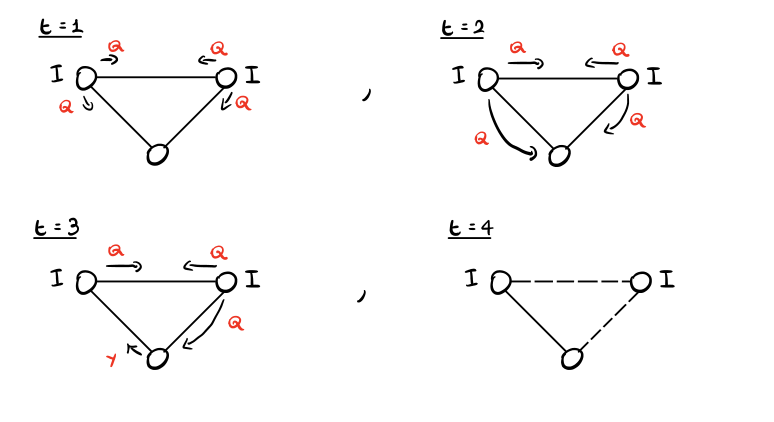
È possibile poi dimostrare che questo non è un caso particolare dello $\text{SHOUT+}$, ma è un risultato più generale. Vale infatti il seguente teorema.

Teorema: Il problema della costruzione distribuita di uno spanning tree non è risolubile in modo deterministico sotto le ipotesi generali con più initiators.

Dimostrazione: Consideriamo la seguente situazione completamente simmetrica in cui abbiamo un triangolo con tre initiators

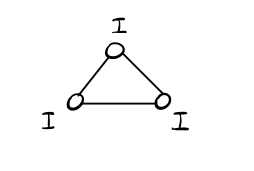
Notiamo che ad ogni $t > 0$ per simmetria tutti i nodi devono necessariamente fare le stesse cose. Ma allora non è possibile rompere la simmetria e costruire uno spanning tree.

\[\tag*{$\blacksquare$}\]