ADRC - 06 - Depth First Traversal
1 Lecture Info
Data:
Capitolo del libro: 2 - Basic Problems and Protocols
In questa lezione abbiamo trattato il problema di come distribuire una risorsa (token) all'interno di una rete distribuita.
2 Depth First Traversal (DFT)
A differenza del problema del broadcast in cui dovevamo condividere una informazione con tutti i nodi nella rete, in questo caso la risorsa che dobbiamo distribuire è gestita in modo mutualmente esclusivo. In particolare quindi esiste una sola copia della risorsa e in un dato istante temporale esiste un solo un nodo che la possiede.
Tra tutti i possibili modi di distribuire il token in questa lezione ci concentreremo su una strategia nota con il nome di depth-first-traversal. L'idea alla base di questa strategia prevede che ogni nodo cerca di inoltrare il token ai suoi vicini fino a quando tutti i nodi a lui adiacenti hanno già ricevuto il token. A quel punto il nodo, che non può più inoltrare il token in "avanti", lo manda "indietro" al nodo che inizialmente lo aveva inoltrato a lui.
Esempio: Il seguente esempio mostra l'ordine in cui i nodi vengono visitati da una depth first traversal, chiamata anche depth first search (DFS)
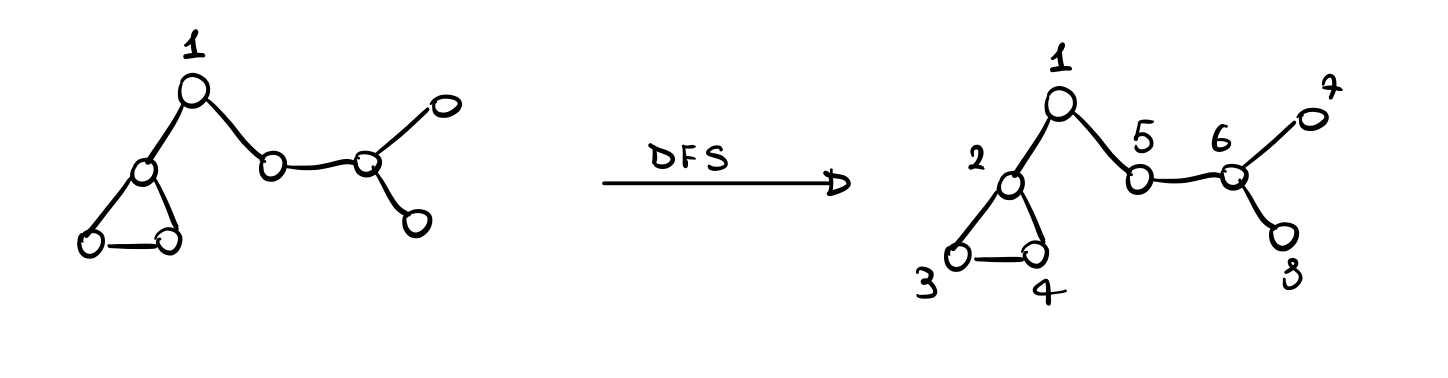
Il problema è quindi definito dalla seguente tripla \(P= \langle P_{init}, P_{final}, R \rangle\) dove,
\(P_{init} = \text{Solo l'initiator ha il token}\)
\(P_{final} = \text{Tutti i nodi hanno ricevuto il token seguendo l'ordine di una DFT}\)
\(R = \begin{cases} \text{Total Reliability (TR)} \\ \text{Bidirectional Link (BL)} \\ \text{Connectivity (CN)} \\ \text{Unique Initiator (UI)} \\ \end{cases}\)
3 Protocollo BACK
Il protocollo più semplice che risolve il problema della DFT può essere descritto come segue:
Quando un nodo riceve il token per la prima volta, ricorda il nodo che gli ha inviato il token (il padre) e comincia ad inoltrare il token ad un suo vicino con il messaggio \(\text{TOKEN}\), aspettando la sua risposta.
Quando il vicino riceve il token, se lo ha già ricevuto lo ritorna immediatamente con un messaggio \(\text{BACK-EDGE}\), altrimenti lo inoltra a tutti i suoi vicini in modo sequenziale, per poi ritornarlo al nodo da cui lo ha ricevuto con un messaggio \(\text{RETURN}\).
Quando il nodo riceve il messaggio \(\text{RETURN}\) dal suo vicino, inoltra il token ad un altro vicino.
Infine, quando il nodo finisce tutti i vicini, invia il messaggio \(\text{RETURN}\) al nodo da cui inizialmente aveva ricevuto il token (il nodo che ha segnato come padre).
Andiamo adesso a formalizzare la strategia appena discussa. Iniziamo notando che il protocollo utilizza i seguenti stati
\(S = \{\text{initiator}, \text{idle}, \text{visited}, \text{done}\}\)
\(S_{init} = \{\text{initiator}, \text{idle}\}\)
\(S_{term} = \{\text{done}\}\)
il comportamento dei nodi invece è descritto dalle seguenti regole
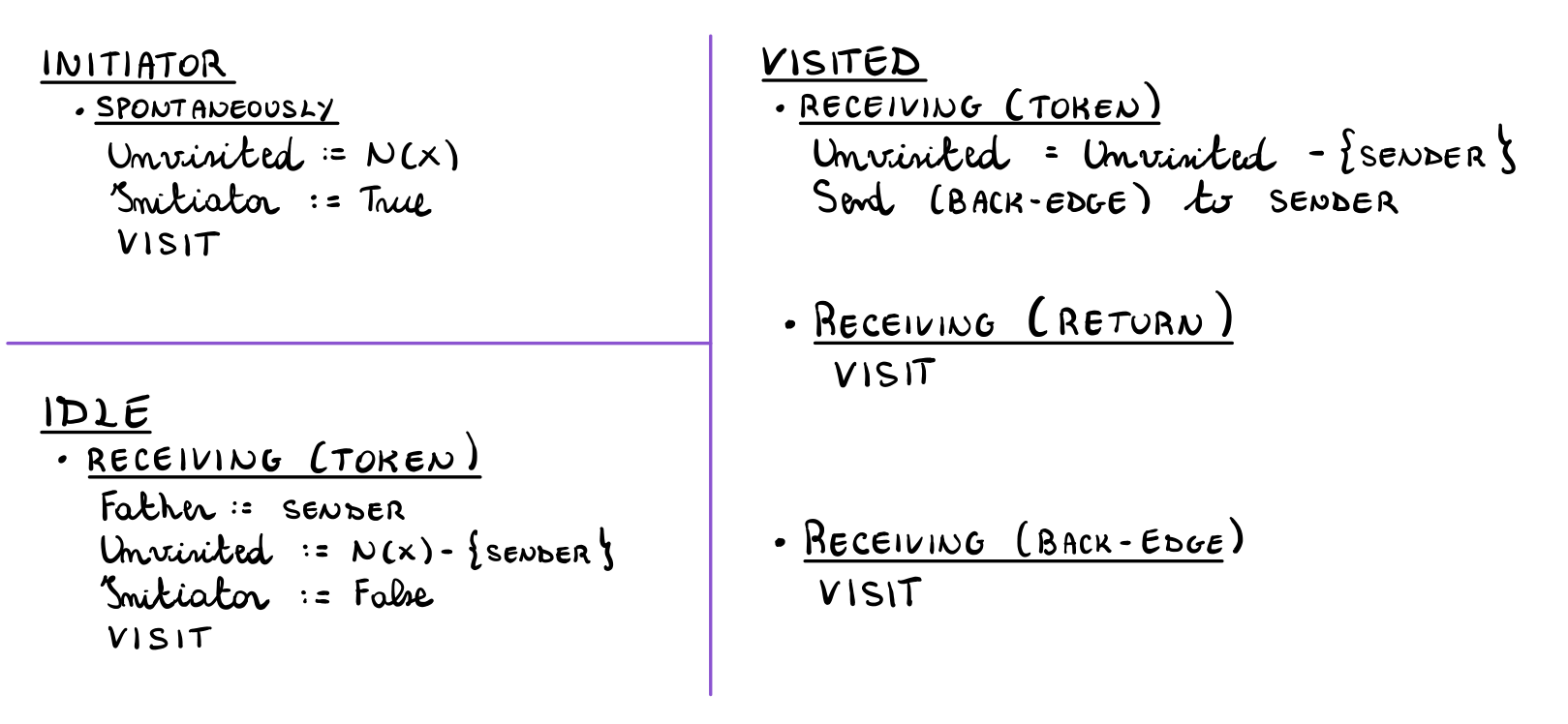
dove VISIT è la procedura utilizzata dai nodi per implementare la
DFT ed è descritta come segue

Andiamo adesso ad analizzare la complessità del protocollo, sia in termini di message complexity sia in termini di ideal time complexity.
3.1 Message Complexity
Notiamo che nel protocollo appena descritto abbiamo tre tipologie di messaggi, che sono:
Token messages: Utilizzati per scambiare il token.
Back-edge messages: Utilizzati per indicare che un nodo ha già ricevuto il token, e che quindi non ne ha bisogno.
Return messages: Utilizzati per ritornare il token dopo averlo ricevuto per la prima volta.
Notiamo che su un dato arco \((x, y) \in E\) possiamo avere una tra le due seguenti possibilità
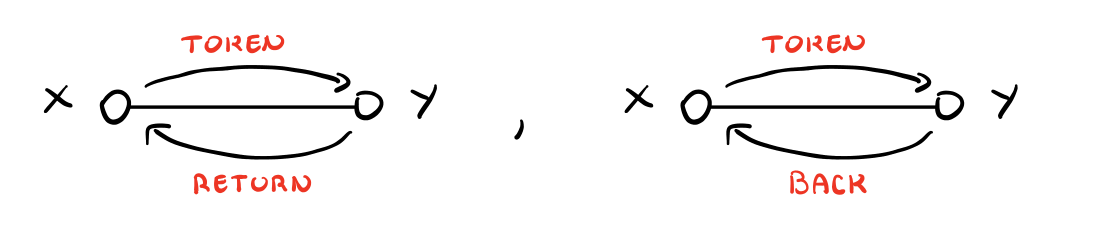
ma allora in ogni arco passano esattamente due messaggi. Troviamo quindi la seguente message complexity
\[M(\text{BACK}) = 2 \cdot m = O(m)\]
Osservazione: Notiamo che \(\Omega(m)\) è un lower bound anche per il problema della DFT. Infatti, risolvendo la DFT stiamo anche risolvendo il Broadcast, e quindi il lower bound del Broadcast si riflette anche nel lower bound del DFT. Questo significa che in termini di message complexity il protocollo \(\text{BACK}\) risulta essere asintoticamente ottimo.
3.2 Ideal Time Complexity
Notiamo che nel protocolo \(\text{BACK}\) ogni nodo esplora in modo sequenziale tutti i suoi vicini. Questo significa che otteniamo la seguente ideal time complexity
\[T(\text{BACK}) = \theta(m)\]
Notiamo però che in termini di ideal time complexity il problema \(DFT\) ha un lower bound di \(\Omega(n)\). Abbiamo quindi un gap abbastanza significativo tra il lower bound e la ideal time complexity del protocollo discusso. L'esplorazione di questo gap ci porta alla definizione di un nuovo protocollo.
4 Protocollo BACK+
Utilizzando il protocollo \(\text{BACK}\) in grafi densi, ovvero grafi con molti archi, la maggior parte del tempo viene speso aspettando la ricezione dei messaggi \(\text{BACK-EDGE}\). Per evitare questo spreco di tempo l'idea è quella di modificare il protocollo \(\text{BACK}\) per eliminare l'invio dei messaggi \(\text{BACK-EDGE}\). In particolare effettuiamo le seguenti modifiche
Quando un nodo \(x\) riceve il token, informa tutto il suo vicinato \(N(x)\) che ha il token.
Tutti i nodi del vicinato \(N(x)\) inviano un messaggio di \(\text{ACK}\) (acknowledgement) al nodo \(x\)
Dopo aver ricevuto tutti gli \(\text{ACKs}\), il nodo \(x\) comincia ad inviare il token ai vicini che non sono ancora stati visitati.
Il protocollo così ottenuto prende il nome di \(\text{BACK+}\). Notiamo che la principale differenza tra i due protocolli è che nel nuovo protocollo i "back-edges" vengono scoperti in parallelo.
4.1 Message Complexity
Questa volta abbiamo quattro tipi di messaggi, che sono: \(\text{TOKEN}, \text{RETURN}, \text{VISITED}, \text{ACK}\).
Iniziamo la nostra analisi notando che tutti i nodi tranne l'initiator ricevono un solo messaggio \(\text{TOKEN}\) e inviano un solo messaggio \(\text{RETURN}\). L'initiator poi non riceve nessun messaggio \(\text{TOKEN}\), e non invia nessun messaggio \(\text{RETURN}\). Questo ci permette di dire che abbiamo esattamente \(2 \cdot (n-1)\) messaggi che sono di tipo \(\text{RETURN}\) o \(\text{TOKEN}\).
Continuando, ogni nodo invia un messaggio \(\text{VISITED}\) a tutti i nodi a lui adiacenti, tranne il nodo da cui ha ricevuto il messaggio. Il totale dei messaggi di tipo \(\text{VISITED}\) è quindi dato da
\[|N(s)| + \sum\limits_{x \neq s} |N(x)| - 1 = 2m - (n-1)\]
Infine, notando che ad ogni messaggio \(\text{VISITED}\) corrisponde un messaggio \(\text{ACK}\), abbiamo che il numero totale di messaggi è dato da
\[M(\text{BACK+}) = \,\,\underbrace{2 \cdot \big[ 2m - (n-1) \big]}_{\text{messaggi di tipo} \\ \text{VISITED e ACK}} \,\,\, + \,\,\, \underbrace{2(n-1)}_{\text{messaggi di tipo} \\ \text{TOKEN e RETURN}} = \,\,\,\, 4m\]
4.2 Ideal Time Complexity
Per quanto riguarda la ideal time complexity, lavorando in un sistema sincrono con un delay di \(\Delta=1\) abbiamo che:
I messaggi \(\text{TOKEN}\) e \(\text{RETURN}\) sono inviati in modo sequenziale, pagando un tempo di \(2(n-1)\).
I messaggi \(\text{VISITED}\) e \(\text{ACK}\) sono inviati in modo parallelo. In particolare ogni nodo spende \(2\) unità di tempo per queste operazioni. Il tempo totale speso tra l'invio e la ricezione di questi messaggi è quindi dato da \(2n\).
In totale troviamo
\[T(\text{BACK+}) = 2 \cdot (n-1) + 2n = 4n - 2\]
il che risulta essere asintoticamente ottimale.
5 Ulteriori Modifiche
Per finire riportiamo alcune ulteriori modifiche che possono essere effettuate al protocollo e che sono riportate nel libro di testo.
5.1 Eliminazione dei messaggi \(\text{ACK}\)
L'idea è quella di eliminare i messaggi \(\text{ACK}\) per diminuire la message complexity.
Notiamo che facendo questa scelta quando un nodo \(x\) invia il messaggio \(\text{VISITED}\) ai suoi vicini non aspetta più la ricezione dei messaggi \(\text{ACK}\) e invia subito il token ad un suo vicino. Questo fatto rende possibile il seguente scenario: consideriamo due nodi \(y\) e \(z\) adiacenti a \(x\). Può succedere che passando da \(y\) il nodo \(z\) riceve il token prima di essere avvisato del fatto che \(x\) ha già avuto il token. In questo caso quindi il nodo \(z\) invierà il token a \(x\), anche se \(x\) lo ha già ricevuto. Graficamente la situazione è descritta come segue,
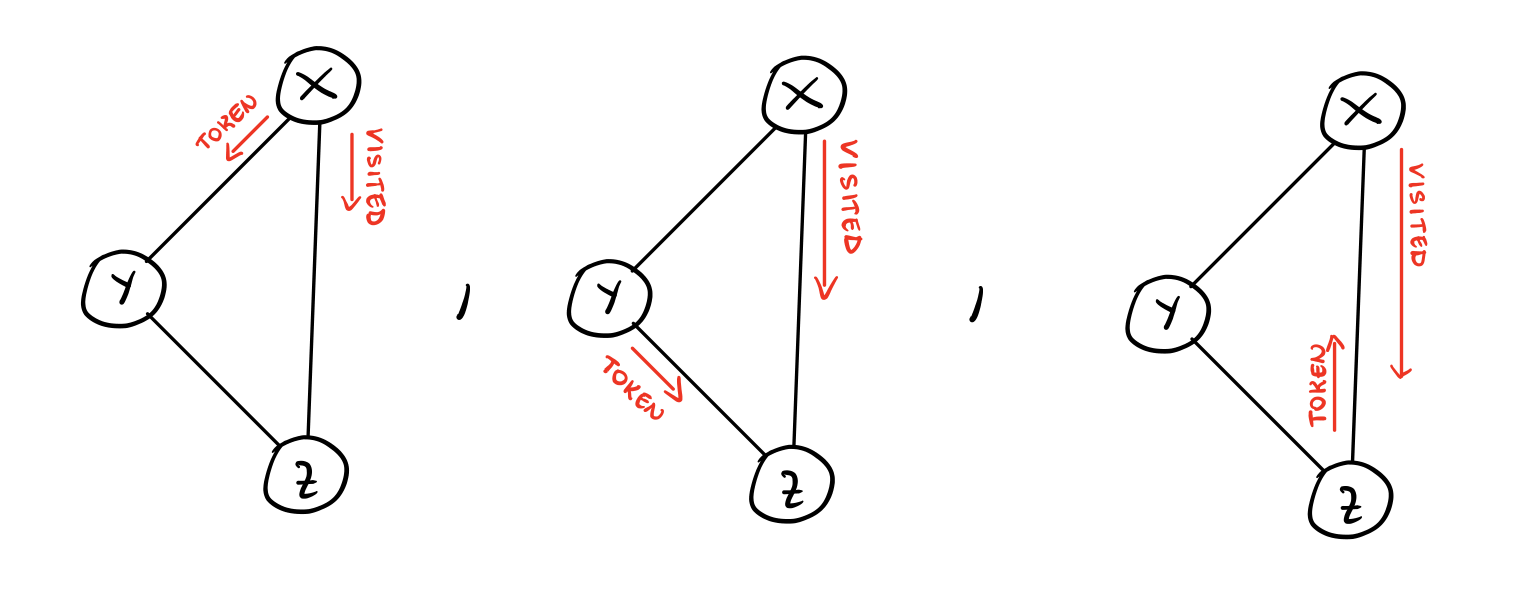
L'idea quindi è che eliminando i messaggi \(\text{ACKs}\) può succedere di inviare più messaggi \(\text{TOKEN}\) di quelli strettamente necessari. Notiamo che al massimo possiamo avere due "errori" per ogni back-edge. In totale quindi possiamo avere al più \(2(m-n+1)\) errori, il che ci fa ottenere una message complexity limitata da
\[\begin{split} M(\text{BACK++}) &\leq M(\text{BACK+}) -\big(2m - (n-1)\big) + 2(m-n+1) \\ &= 4m -\big(2m - (n-1)\big) + 2(m-n+1) \\ &= 4m -n +1 \end{split}\]
Per quanto riguarda l'ideal time complexity, abbiamo che ogni nodo non deve più aspettare due unità di tempo, ma solo una unità di tempo per inviare il messaggio \(\text{VISITED}\). Questo significa anche che può inviare il token (o il messaggio \(\text{RETURN}\) se non ha vicini da visitare) in modo sincrono all'inivio del messaggio \(\text{VISITED}\).
Infine, considerando il fatto che per definizione in un sistema asincrono non ci possono essere ritardi, non ci possono neppure essere errori. Troviamo dunque il seguente risultato
\[T(\text{BACK++}) = 2\cdot(n-1) = 2n - 2\]
5.2 Eliminazione dei messaggi \(\text{Visited}\)
Come ultima modifica che possiamo fare al protocollo per diminuire ulteriormente la message complexity l'idea è quella di eliminare i messaggi \(\text{VISITED}\), e utilizzare i messaggi \(\text{TOKEN}\) per dire in modo implicito che il nodo è stato già visitato.
Notiamo che questo salvataggio di messaggi avviene solamente per i nodi che, quando ricevono il token, hanno dei vicini che devono essere ancora visitati. Indichiamo con \(f_{*}\) il numero di questi nodi. Segue che il numero di messaggi che salviamo è dato da \(n - f_{*}\).
In totale quindi, con questa ulteriore modifica, riusciamo ad avere una message complexity di
\[M(\text{Back}_*) = 4m -n + 1 - (n - f_*) = 4m -2n + f_* + 1\]
Osservazione: Notiamo che il valore di \(f_*\), a differenza dei valori di \(m\) ed \(n\), non è un parametro del sistema, ma dipende dalla particolare esecuzione che si sta analizzando. In generale quando abbiamo a che fare con valori che cambiano a seconda della particolare esecuzione, indicheremo tali valori con il subscript \(*\).