AGT - 01 - Introduzione alla AGT
Lecture Info
Data:
Sito corso: AGT_2018
Slides: 01 - Introduction
Introduzione: In questa lezione abbiamo introdotto i concetti fondamentali della algorithmic game theory.
1 La nascita della Algorithmic Game Theory
L'algorithmic game theory (AGT) nasce dalla combinazione della teoria dei giochi con la teoria degli algoritmi.
Ricordiamo che la teoria degli algoritmi cerca di rispondere a problemi di natura computazionale, tra cui troviamo anche i seguenti:
Cosa può essere computato? (Theory of comutation, Turing machines, Halting problem)
Quante risorse sono necessarie per calcolare una soluzione? (Complexity Theory, NP-completeness)
Qual è la qualità della soluzione calcolata rispetto a quella ottima? (Approximation algorithms)
Che modello di calcolo si utilizza? (Central model, Distributed model)
La teoria dei giochi invece è nata dopo la pubblicazione del libro "Games and Economic Behavior", co-scritto da John Von Neumann nel 1944, e si occupa di analizzare le interazioni che avvengono tra individui egoistici. Tra le problematiche affrontate dalla teoria dei giochi troviamo anche le seguenti:
Qual è il risultato (outcome) dell'interazione?
Quali social goals sono compatibili con l'egoismo dei giocatori?
Prese singolarmente le due teorie fanno ciascuna delle particolari assunzioni:
Theory of Algorithms (Distributed systems):
I processori sono obedient, faulty o adversarial.
I sistemi di interesse sono grandi e dispongono di risorse computazionali limitate.
Game Theory:
I giocatori sono strategici.
I sistemi di interesse sono piccoli e dispongono di risorse potenzialmente illimitate.
Con l'avvento di Internet si sono venuti a creare molti sistemi contenti tanti utenti, ciascuno dei quali dispone di risorse limitate che deve utilizzare al fine di soddisfare determinati obiettivi egoistici. Sono quindi nati una serie di problemi in cui è di fondamentale importanza gestire bene sia gli aspetti strategici degli utenti e sia quelli computazionali delle risorse utilizzate. La AGT studia proprio questa tipologia di problemi.
L'AGT presenta quindi un ponte che connette queste due teorie tra loro. Mentre la GT (Game Theory), offre una serie di concetti e strumenti utili per risolvere problemi computazionali in scenari non-cooperativi, la TA (Theory of Algorithms) permette di interpretare e dare senso ad alcuni risultati della GT classica.
2 Game Theory Basics
Informalmente un gioco è composto dai seguenti elementi:
Un insieme di players.
Un insieme di strategie, che vengono utilizzate per specificare varie cose, tra cui chi esegue una particolare azione, quando la esegue, e quali azioni può esegure.
Per ogni possibile combinazione di strategie è necessario specificare il particolare payoff per ogni singolo giocatore.
Un insieme di outcomes, detti anche profili di strategia, che rappresentano le azioni che verranno effettivamente compiute dai vari giocatori.
La teoria dei giochi classica cerca di predirre, qualora fosse possibile, l'outcome del gioco, chiamato anche la soluzione (solution), considerando le possibili strategie e il comportamento individuale dei giocatori, assunti essere giocatori razionali.
2.1 Esempi
Per capire meglio il concetto di gioco, andiamo a vedere due classici esempi.
2.1.1 The Prisoner's Dilemma
In questo primo gioco abbiamo due persone, i giocatori, che sono stati imprigionati per aver commesso un crimine assieme. A ciascun giocatore è data la possibilità di denuncinare (implicate) l'altro giocatore al fine di avere una riduzione della propria pena.
Il gioco può essere modellato con la seguente matrice di payoffs
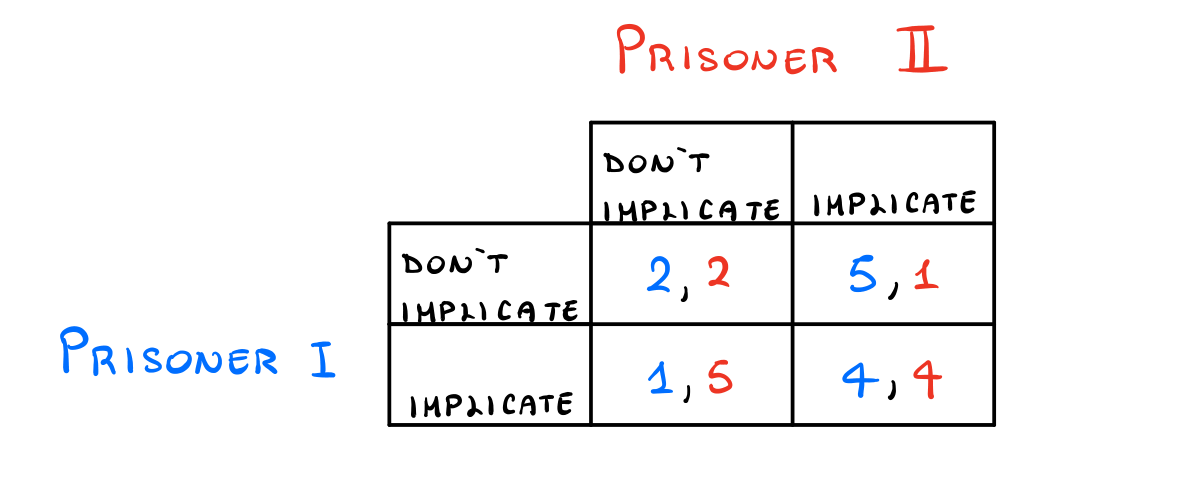
La matrice è letta nel seguente modo: ciascun giocatore ha due possibili strategie, che sono implicate, ovvero denuncia, e don't implicate, ovvero non denuncia. Per ciascuna delle 4 possibili combinazioni ci sono una coppia di numeri, che rappresentano gli anni di galera da scontare per ciascun giocatore. Se il prisoner I sceglie implicate e anche il prisoner II sceglie implicate, allora entrambi si fanno \(4\) anni di galera. Se invece il prisoner I sceglie implicate e il prisoner II sceglie don't implicate, allora il prisoner I si fa solo \(1\) anno di galera, mentre il prisoner II si fa ben \(5\) anni di galera.
A questo punto ci possiamo chiedere: come si dovrebbe comportare il prisoner I? A tale fine analizziamo le possibili strategie del prisoner II:
Se il prisoner II sceglie don't implicate allora la scelta migliore è implicate.
Se il prisoner II sceglie implciate allora la scelta migliore è implicate.
Indipendentemente dalle azioni prese dal prisoner II, al prisoner I conviene sempre di scegliere implicate. In questo caso si dice che implicate è una dominant strategy per il prisoner I, nel senso che è la strategia migliore che il giocatore I può scegliere, indipendentemente dalla scelta del giocatore II. Dato poi che lo stesso ragionamento può essere fatto per il prisoner II, abbiammo che implicate è una dominant strategy anche per il prisoner II, e dunque per tutti i giocatori. In questo caso particolare diciamo che implicate è un dominant strategy equilibrium.
2.1.2 A Network Game
Consideriamo la seguente rete fisica, costruita da due diversi ISPs (Internet Service Providers)
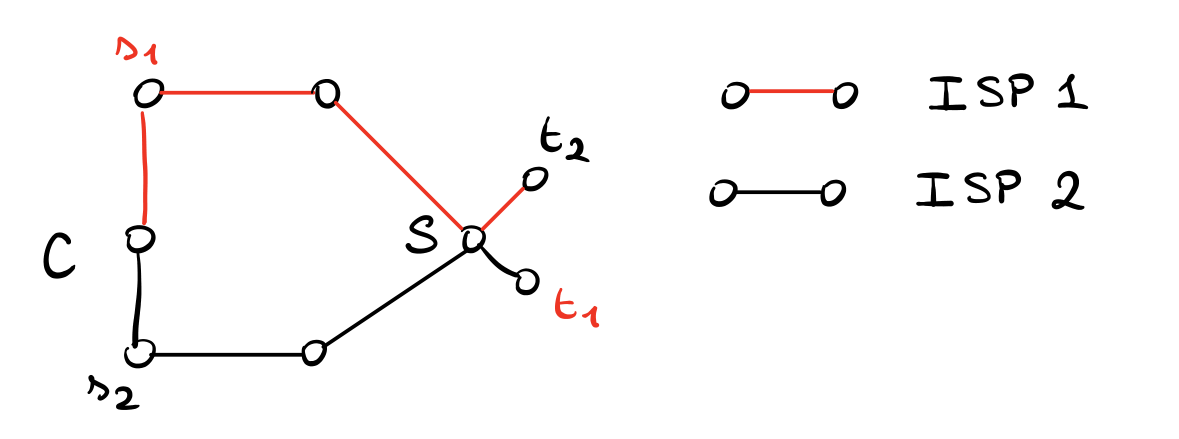
Supponiamo che ISP1 vuole inviare un msg da \(s_1\) a \(t_1\), mentre ISP2 ne vuole inviare uno da \(s_2\) a \(t_2\). Per fare questo ciascun ISP può utilizzare due cammini: o quello che passa per \(C\) oppure quello che passa per \(S\). Ciascun ISP paga il trasporto del messagio solamente quando si utilizzano gli archi posseduti dal particolare ISP. Notiamo infine come il tratto finale che collega \(S\) a \(t_2\) e \(t_1\) è talmente breve che il costo di utilizzo degli archi non viene considerato.
Troviamo quindi la seguente matrice di payoff
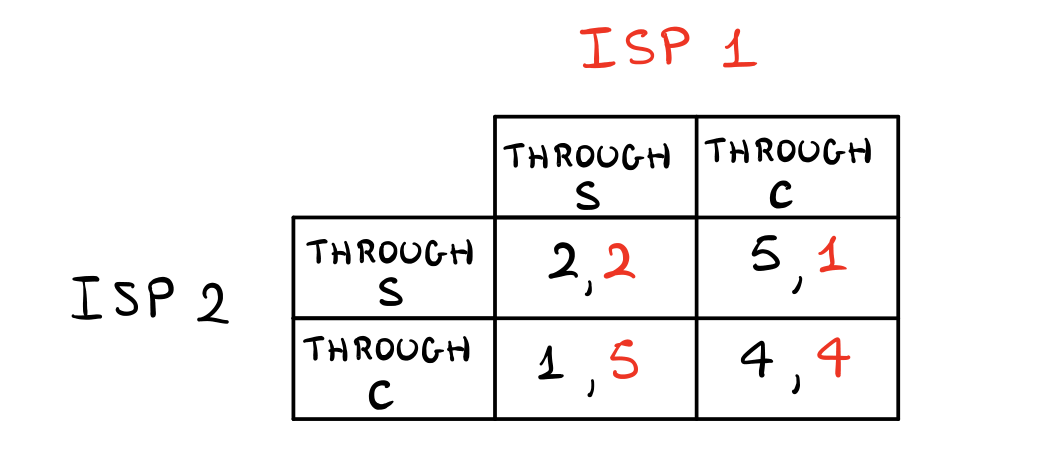
La matrice è identica a quella vista nel precedente esempio. Dunque, eseguendo lo stesso ragionamento svolto prima possiamo quindi concludere che a ciascun ISP conviene sempre utilizzare gli archi dell'altro ISP, andando a pagare \(4\).
3 Normal Form of a Game
Andiamo adesso a formalizzare quanto visto prima.
Def: Formalmente rappresentiamo un gioco utilizzando i seguenti elementi:
\(N\) giocatori, assunti razionali;
\(S_i\) insieme di possibili strategie per il giocatore \(i\);
Una matrice di payoff che descrive l'associazione
\[(s_1, s_2, \ldots, s_N) \to (p_1, p_2, \ldots, p_N)\]
Dove \((s_1, s_2, \ldots, s_N)\) rappresenta una combinazione di strategie e viene utilizzata per descrivere il comportamento di ciascun giocatore, mentre \((p_1, p_2, \ldots, p_N)\) descrive il payoff di ogni singolo giocatore.
Questa rappresentazione per un gioco è anche detta normal form. Seguono alcune fondamentali definizioni rispetto al concetto di equilibrio per un gioco.
3.1 Dominant Strategy Equilibrium
Un dominant strategy equilibrium (DSE) è una combinazione di strategie \(s^* = (s_1^*, s_2^*, \ldots, s_N^*)\) tale che \(s^*\) è una dominant strategy per ogni giocatore \(i\), ovvero tale che per ogni possibile profilo di strategie alternativo \(s = (s_1, s_2, \ldots, s_i, \ldots, s_N)\) si ha che
Se il payoff \(p_i\) è una utility, allora
\[p_i(s_1, s_2, \ldots , s_i^*, \ldots, s_N) \geq p_i(s_1, s_2, \ldots, s_i, \ldots, s_N)\]
Se il payoff \(p_i\) è un costo, allora
\[p_i(s_1, s_2, \ldots , s_i^*, \ldots, s_N) \leq p_i(s_1, s_2, \ldots, s_i, \ldots, s_N)\]
Detto altrimenti, una dominant strategy è la migliore risposta a qualunque strategia degli altri giocatori. Tipicamente se un gioco ha un DSE, i giocatori convergono quasi immediatamente ad esso. Detto questo, non tutti i giochi hanno un DSE. A tale fine viene risulta fondamentale utilizzare una versione più rilassata di equilibrio, introdotto con la seguente definizione
3.2 Nash Equilibrium
Un equilibrio di nash (NE) è una combinazione di strategie \(s^* = (s_1^*, s_2^*, \ldots, s_N^*)\) tale che per ogni giocatore \(i\), la strategie \(s_i^*\) è la migliore risposta alle scelte degli altri giocatori \((s_1^*, \ldots, s_{i-1}^*, s_{i+1}^*, \ldots, s_N^*)\), ovvero tale che per ogni altra possibile strategia \(s_i\) per il giocatore \(i\), si ha
Se il payoff \(p_i\) è una utility, allora
\[p_i(s_1^*, s_2^*, \ldots , s_i^*, \ldots, s_N^*) \geq p_i(s_1^*, s_2^*, \ldots, s_i, \ldots, s_N^*)\]
Se il payoff \(p_i\) è un costo, allora
\[p_i(s_1^*, s_2^*, \ldots , s_i^*, \ldots, s_N^*) \leq p_i(s_1^*, s_2^*, \ldots, s_i, \ldots, s_N^*)\]
Notiamo che se un profilo di strategie è un DES, allora è anche un NE, ma non vale il viceversa. Inoltre, se un gioco viene giocato ripetutamente e i giocatori convergono ad una soluzione, allora la combinazione di strategie finali che rappresenta la soluzione è un NE.
Esempio Consideriamo la seguente situazione, chiamata "The Battle of the Sexes" e descritta dalla seguente matrice di payoffs
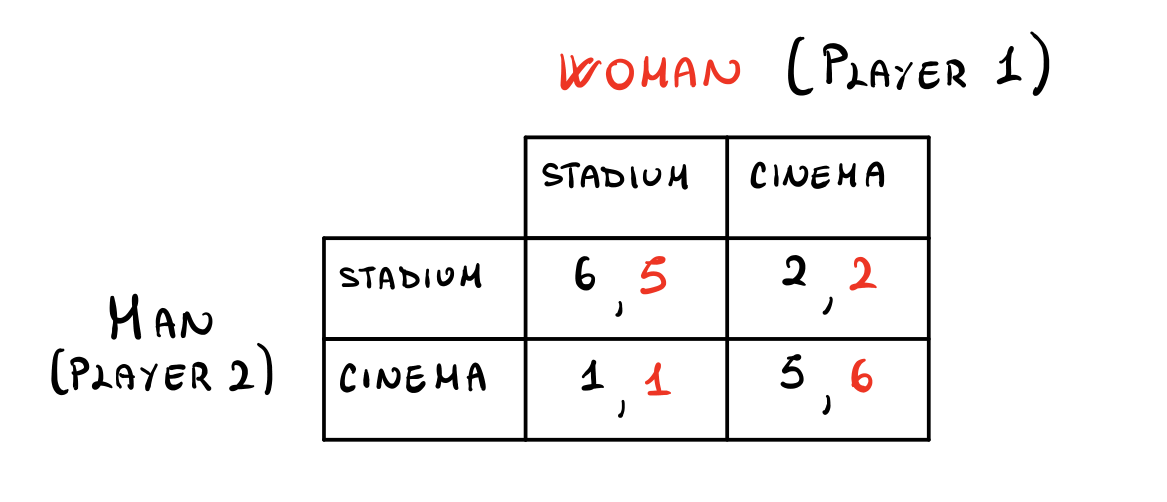
Notiamo che i profili di strategie (Stadium, Stadium) e (Cinema, Cinema) sono degli equilibri di Nash, ma non sono DSE.
4 Equilibri di Nash
Andiamo adesso ad analizzare gli aspetti di esistenza e qualità rispetto ai possibili equilibri di nash per un dato gioco.
4.1 Esistenza
per i giochi detti pure strategies games, che sono caratterizzati dal fatto che ciascun giocatore sceglie in modo deterministico una strategia, non esiste un risultato generale per l'esistenza di un equilibrio di nash (NE). In altre parole, si potrebbero avere i tre seguenti casi:
Non esiste nessun NE;
Ne esiste uno solo;
Ne esistono più di uno;
Se però consideriamo mixed strategies games, che introducono una variabilità aleatorie alle varie strategie dei giocatori, allora esiste un teorema, dimostrato nel 1951 da Nash per la sua tesi di dottorato, che afferma l'esistenza di un equilibrio in cui ciascun giocatore massimizza il suo valore atteso.
Esempio: Consideriamo la seguente payoff matrix
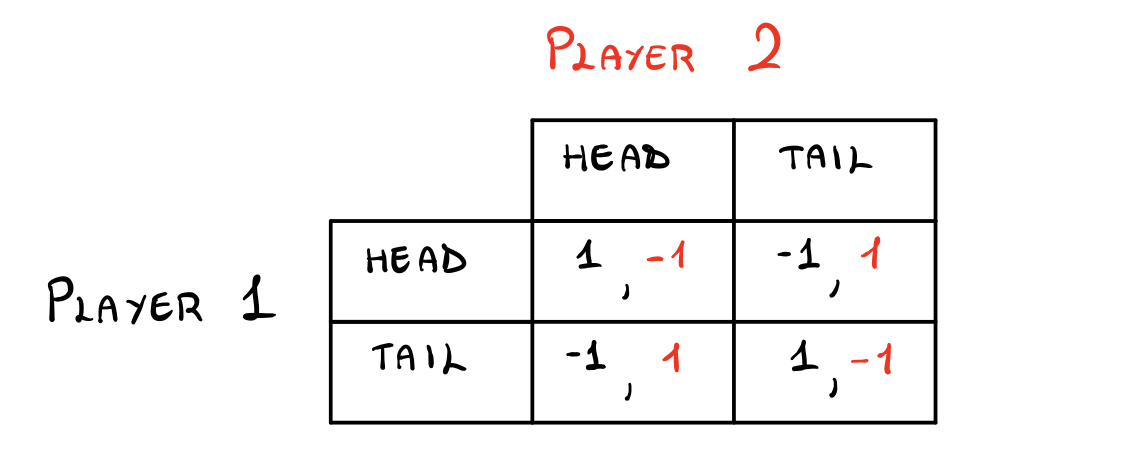
Notiamo che questo gioco non ammette nessun NE in quanto in ogni profilo di strategie ad almeno uno dei due giocatori conviene cambiare strategia.
4.2 Qualità
Una volta trovato un NE ci possiamo domandare quanto peggiore è il NE trovato rispetto ad una situazione idealizzata in cui i giocatori collaborano tra loro per ottenere il risultato migliore.
Per confrontare outcome diversi necessitiamo di una social-choice function \(C\) che ci permette di associare un numero reale ad ogni proflio di strategie, pertmettendoci così facendo di misurare la qualità complessiva di un outcome \(S\). Un tipico esempio di social-choice function è la seguente
\[C(S) := \text{ sum of all players costs and utilities }\]
4.2.1 Price of Anarchy (PoA)
Il PoA ci da un upper bound alla soluzione trovata giocando rispetto all'outcome migliore. Formalmente è definito come segue
Def: Dato un gioco \(G\) e una social-choice function \(C\), sia \(S\) l'insieme di tutti gli equilibri di nash. Se il payoff è un costo per i giocatori, sia OPT l'outcome del gioco \(G\) che minimizza la funzione \(C\). Definiamo quindi il price of anarcy (PoA) di \(G\) rispetto a \(C\) nel seguente modo
\[\text{PoA}_G(C) = \sup_{s \in S} \frac{C(s)}{C(OPT)}\]
4.2.2 Price of Stability (PoS)
Il PoS invece è definito come il rapporto tra il "migliore" NE secondo C e l'outcome ottimo OPT sempre secondo C. In formula,
\[\text{PoS}_G(C) := \inf_{s \in S} \frac{C(s)}{C(OPT)}\]
Sempre nel caso in cui il payoff rappresenta un costo.
4.2.3 Osservazioni generali
Seguono alcune osservazioni generali su PoA e PoS:
PoA e PoS sono \(\geq 1\) per problemi di minimizzazione e \(\leq 1\) per problemi di massimizzazione;
PoA e PoS sono bassi quando sono vicini ad 1;
Se il gioco presenta un solo equilibrio, allora PoA = PoS.
Il concetto di PoA è simile al concetto di approximation ratio di una euristica.
Limitare il PoS è un risultato più debole rispetto a limitare il PoA. In alcuni casi però è possibile limitare solamente il PoS.
5 Note Finali
5.1 Selfish Routing: Pigou's game
Possiamo rappresentare il traffico in una rete tramite un gioco, in cui i giocatori sono gli utenti della rete e le strategie sono i cammini della rete in cui gli utenti possono redirigere il loro traffico.
Per fare un esempio, nel gioco di Pigou [1920], abbiamo la seguente rete
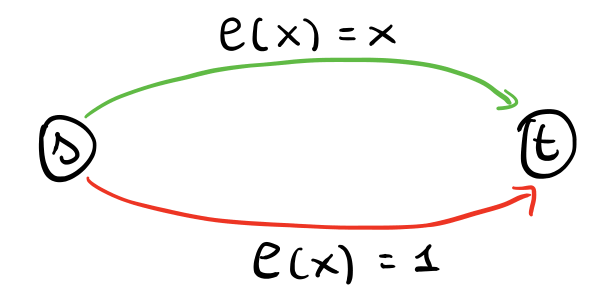
Abbiamo \(1\) unità di traffico che deve passare da \(s\) a \(t\). Notiamo come il costo dell'arco verde dipende dalla congestione dell'arco, ovvero dalla frazione del flusso totale che passa sull'arco, mentre il costo dell'arco rosso è fisso.
L'unico NE di questo gioco è quello in cui tutto il flusso passa sull'arco verde. Il costo di questo equilibrio è
\[1 \cdot 1 + 0 \cdot 1 = 1\]
Per capire il costo minimo in una situazione di cooperazione ideale dobbiamo capire il valore \(x\) che minimizza la funzione \(C(x) := x \cdot x + 1 \cdot (1 - x)\) per \(x \in [0, 1]\). Prendendo la derivata prima otteniamo che
\[C'(x) = 2x - 1 = 0 \iff x = \frac12\]
dunque la situazione idale è quella in cui il flusso viene diviso equiamente nei due archi. Il costo di questa soluzione è
\[C(OPT) = C\Big(\frac12\Big) = \frac14 + \frac12 = \frac34\]
Troviamo quindi
\[\text{PoA} = \text{PoS} = \frac{1}{\frac34} = \frac43\]
Teorema (Roughgarden & Tardos, 2000): The PoA of the selfish routing game with linear latency function is at most \(4/3\).
5.2 The Braess's Paradox
Abbiamo già visto vari esempi che fanno vedere come il comportamento egoistico dei giocatori assume un ruolo importante nel modo in cui una rete viene utilizzata. Non dovrebbe sorprendere quindi osservare il fatto che anche quando bisogna progettare una rete risulta fondamentale tenere in considerazione il comportamento egoista dei futuri utilizzatori della rete.
Per fare un esempio concreto, consideriamo la seguente rete
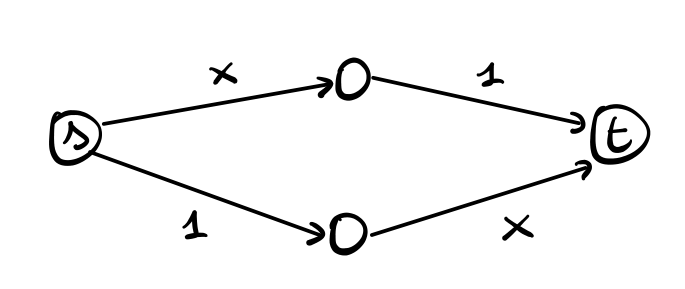
e supponiamo di dover spostare \(1\) unità di traffico da \(s\) a \(t\). Ciascun giocatore gestisce una frazione infinitesimale del traffico, e l'obiettivo di ciascun giocatore è minimizzare il proprio costo.
Notiamo che con la rete così definita, l'unico NE è quello in cui il flusso viene diviso in modo equo
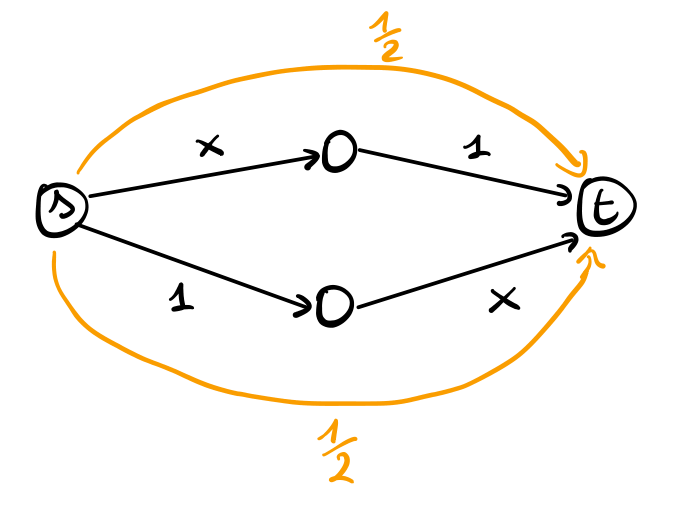
L'average travel time associato a questo equilibrio è anche l'outcome migliore, in quanto è pari a
\[\frac12 \cdot \frac12 + \frac12 \cdot 1 + \frac12 \cdot \frac12 + \frac12 \cdot 1 = \frac12 + 1 = 1.5\]
Supponiamo adesso che, al fine di diminuire l'average travel time, andiamo ad aggiungere un arco speciale di costo \(0\)
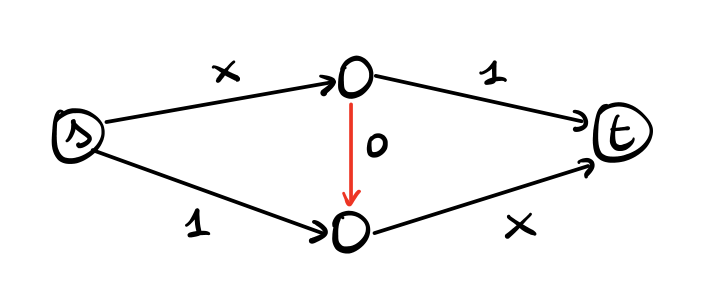
Osserviamo come ora l'unico NE è quello in cui tutto il flusso va nell'arco di costo \(0\). Così facendo quindi l'average travel time è diventato
\[1 \cdot 1 + 1 \cdot 0 + 1 \cdot 1 = 2\]
mentre il costo ottimale è sempre \(1.5\), ottenuto dividendo a metà il flusso. Con questo cambiamento, intuitivamente buono, abbiamo invece incrementato il PoA e il PoS
\[\text{PoA} = \frac{2}{\frac32} = \frac43 > 1\]
In altre parole, abbiamo peggiorato il modo in cui la rete viene utilizzata.
5.3 Schema del corso
Nel corso studieremo due aree diverse della AGT, che sono:
Mechanism design, che si occupa della creazione di giochi in modo da garantire determinate proprietà.
Studio di PoS e PoA su giochi inspirati a problemi di natura informatica. Questo tipo di analisi verrà fatta utilizzando il seguente schema:
Si considera una situazione esterna e la si modella come gioco;
Si verifica l'esistenza di eventuali NE;
Se esistono NE si verifica se siamo in grado di calcolarli, e ci occupiamo anche di come farlo;
Compariamo la qualità di un NE rispetto ad una situazione ideale in cui gli agenti possono anche collaborare (cooperative system).
Giocando in modo ripetuto cerchiamo di stabilire se e in quanti passi è possibile calcolare un NE.
5.4 Esercizi
Pollution Game: Abbiamo \(n\) nazioni, ciascuna delle quali può scegliere di controllare il proprio inquinamento oppure no. Il controllo dell'inquinamento ha un costo di \(3\) per la nazione, mentre ciascuna nazione che non controlla il proprio inquinamento aggiunge un cosot di \(1\) a tutte le nazioni.
Provare a dare dei bounds per la PoS e la PoA.
Tragedy of Commons: Abbiamo \(n\) players che vogliono comunicare utilizzando 1 canale condiviso con una capacità massima di 1 unità.
Il giocatore \(i\) vuole inviare \(x_i\) unità di flusso nel canale, con \(x_i \in [0, 1]\). Ogni giocatore vuole massimizare il contenuto inviato, ma la qualità del canale si deteriora all'aumentare del traffico totale inviato. Formalmente, il valore del giocatore \(i\) è definito come segue
\[x_i \Big(1 - \sum_j x_j\Big)\]
Provare a dare dei bounds per la PoS e la PoA.