AGT - 03 - Local Connection Game
1 Local Connection Game
Il Local Connection Game (LCG) fa parte dei Network Formation Games introdotti la scorsa lezione, è stato introdotto da Fabrikant et al. (2003) ed è così descritto:
Abbiamo \(n\) giocatori, ciascuno dei quali rappresenta un nodo di un grafo che deve essere costruito.
La strategia del giocatore \(u\) consiste nello scegliere un insieme di archi non diretti da costruire. Tutti gli archi scelti devono essere incidenti al nodo \(u\). La costruzione di ogni arco ha un costo di \(\alpha\).
Dato un profilo di strategie \(S\), il grafo costruito viene indicato con \(G(S)\) ed è costituito dall'insieme dei nodi (un nodo per giocatore), e da tutti gli archi \((u, v)\) che sono stati costruiti almeno da uno dei due giocatori \(u\), \(v\).
L'obiettivo del giocatore \(u\) consiste nel minimizzare la distanza verso gli altri nodi, cercando al contempo di pagare il meno possibile. Formalmente il giocatore \(u\) vuole minimizzare il proprio costo
\[\text{COST}_u(S) := \alpha \cdot n_{u} + \sum_{v} \text{dist}_{G(S)}(u, v)\]
dove, \(n_u\) indica il numero di archi comprati dal giocatore \(u\) nel profilo \(S\), mentre \(\text{dist}_{G(S)}(u, v)\) indica la lunghezza di un qualsiasi cammino minimo tra \(u\) e \(v\) nel grafo \(G(S)\).
1.1 Esempio
Consideriamo la seguente rete
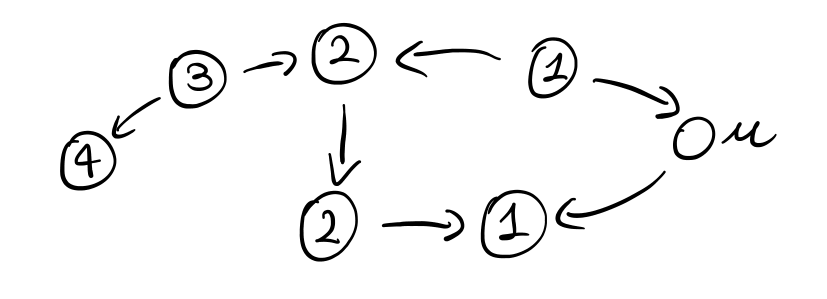
In questa rete il costo del nodo \(u\) è dato da
\[C_u = \alpha + (1 + 1 + 2 + 2 + 3 + 4) = \alpha + 13\]
Se poi \(u\) costruisce un arco verso il nodo più distante, otteniamo la seguente rete
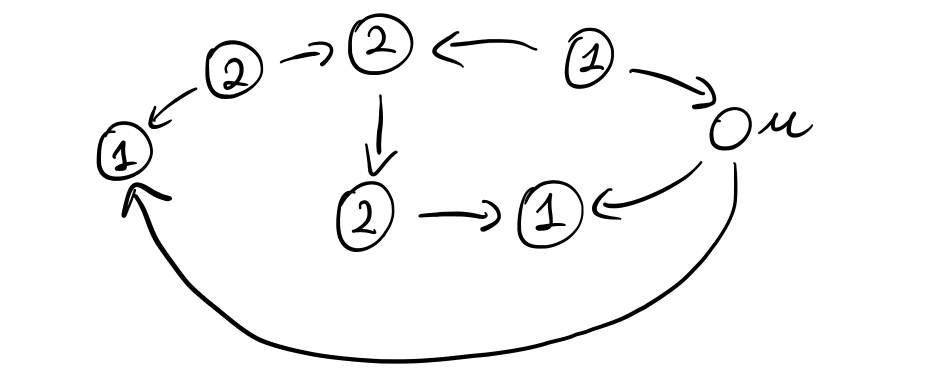
Adesso il nodo \(u\) paga
\[C_u = 2 \cdot \alpha + (1 + 1 + 2 + 2 + 1 + 2) = 2\alpha + 9\]
1.2 Obiettivi Analisi
Come per il Global Connection Game (GCG) analizzato la scorsa lezione, come soluzione per il LCG consideriamo gli equilibri di nash (NE), mentre come costo sociale consideriamo la somma die costi dei giocatori. Il costo sociale di un profilo \(S\) sarà indicato con \(SC(S)\). Seguono quindi delle definizioni utili
Def. 1: Una rete \(G(S)\) è ottimale se minimizza il costo sociale.
Def. 2: Un grafo \(G = (V, E)\) è stabile per un \(\alpha\) se esiste un profilo di strategie \(S\) tale che \(S\) è un NE per il LCG e \(G(S) = G\).
Osserviamo che
In \(SC(S)\), ogni termine \(\text{dist}_{G(S)}(u, v)\) appare esattamente due volte.
In una rete stabile ogni arco \((u, v)\) è comprato al massimo da un gicatore.
Ogni rete stabile è necessariamente connessa.
Da queste osservazioni otteniamo che il costo sociale di una rete stabile \(G(S) = (V, E)\) è dato da
\[SC(S) = \alpha \cdot |E| + \sum_{u, v \in V} \text{dist}_{G(S)}(u, v)\]
Al fine di dare dei bounds per il PoS e il PoA del gioco, andiamo a studiare la struttura delle reti ottime al variare del parametro \(\alpha\).
2 Struttura delle Reti Ottime
La struttura della rete ottima, ovvero della rete che minimizza il costo sociale, dipende ovviamente dal paremetro \(\alpha\). Più \(\alpha\) è baso e più ai nodi conviene comprare tanti archi. Viceversa, più \(\alpha\) è alto e più ai nodi conviene comprare pochi archi. Intuitivamente quindi ci aspettiamo la seguente situazione
Se \(\alpha >> 1\), ovvero se \(\alpha\) è molto grande, allora la rete ottima è il grafo a stella.
Se \(\alpha << 1\), ovvero se \(\alpha\) è molto piccolo, allora la rete ottima è il grafo completo.
Volendo formalizzare questa intuzione è possibile dimostrare il seguente teorema.
Teorema: Se \(\alpha \leq 2\), il grafo completo è una soluzione ottima, mentre se \(\alpha > 2\) ogni grafo a stella è una soluzione ottima.
dim: Sia \(G = (V, E)\) una soluzione ottima, e definiamo \(m := |E|\), \(OPT = SC(G)\). Qualsiasi sia questa soluzione ottima, Vale sicuramente il seguente lower bound
\[OPT \geq \alpha m + 2m + 2 \Big[n(n - 1) - 2m \Big]\]
Infatti abbiamo che \(\alpha m\) è il costo per costruire \(m\) archi, ogni arco costruito unisce due nodi direttamente, andando quindi ad influire \(2m\) nel costo sociale, e infinie le restanti coppie di nodi, che sono \(n (n - 1) - 2m\), si trovano ad una disatnza \(\geq 2\).
Segue quindi che
\[OPT \geq LB(m) := (\alpha - 2) m + 2n (n-1) \geq \min_m LB(m)\]
Andiamo adesso ad analizzare i due casi separati, a seconda del valore di \(\alpha\):
Se \(\alpha \geq 2\), allora \(LB(m)\) raggiunge il minimo quando \(m = n-1\), e quindi
\[\begin{split} OPT &\geq (\alpha - 2)(n - 1) + 2n(n-1) \\ &= \text{costo sociale di un qualsiasi grafo a stella con } n \text{ nodi} \end{split}\]
Dunque se \(\alpha \geq 2\) non possiamo fare di meglio di una stella.
Se invece \(\alpha \leq 2\), allora per minimizzare \(LB(m)\) dobbiam massimizzare \(m\). Dato che il massimo valore assegnabile ad \(m\) è proprio \(m = n(n-1)/2\), troviamo che
\[\begin{split} OPT &\geq LB\Big(\frac{n(n-1)}{2}\Big) \\ &= \text{costo sociale di un grafo completo con } n \text{ nodi} \end{split}\]
Dunque se \(\alpha \leq 2\) non possiamo fare di meglio di un grafo completo.
\[\tag*{$\blacksquare$}\]
2.1 Ottimili Sociali Stabili
Andiamo adesso a vedere quando questi ottimi sociali sono anche reti stabili. A tale fine vale il seguente teorema.
Teorema: Se \(\alpha \leq 1\), il grafo completo è stabile, mentre se \(\alpha \geq 1\), ogni grafo a stella è stabile.
dim: Dimostriamo per casi
Se \(\alpha \leq 1\), dato un profilo \(S\) che costruisce un grafo completo \(G(S) = K_n\), a nessun giocatore \(v\) conviene togliere qualche arco, in quanto risparmierebbe \(\alpha\) ma andrebbe a pagare \(\geq 1\). Dunque \(S\) è un NE e \(K_n\) è una rete stabile.
Se invece \(\alpha \geq 1\), consideriamo un profilo \(S\) che costruisce una rete a stella
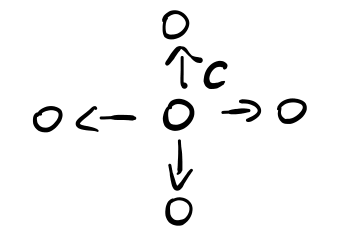
Notiamo che \(C\) non ha interesse a rimuovere qualche arco, in quanto altrimenti il grafo diventerebbe disconnesso. Lo stesso vale per un generico nodo \(v\), in quanto se \(v\) compra \(k\) archi paga \(\alpha \cdot k\), e risparmia \(k\), il che non conviene.
\[\tag*{$\blacksquare$}\]
3 Upper Bound on PoS
Andiamo a dimostrare il seguente teorema, che pone un upper bound al Price of Stability del LCG.
Teorema: per \(\alpha \leq 1\) e \(\alpha \geq 2\), il PoS è \(1\), mentre per \(\alpha \in (1, 2)\), il PoS è al più \(\frac43\).
Dim: Dai due risultati precedenti segue che per \(\alpha \leq 1\) e \(\alpha \geq 2\), il migliore NE genera la rete ottima, e quindi il PoS è \(1\).
Nel caso \(1 < \alpha < 2\) invece abbiamo che la soluzione ottima è il grafo completo, mentre ogni grafo a stella \(T\) è stabile. Troviamo quindi il seguente upper bound
\[\text{PoS} \leq \frac{SC(T)}{SC(K_n)} = \frac{(\alpha - 2)(n - 1) + 2n(n - 1)}{\alpha \cdot \frac{n(n-1)}{2} + n(n-1)}\]
L'espressione più a destra poi è massimizza per \(\alpha \to 1\)
\[\begin{split} \frac{(\alpha - 2)(n - 1) + 2n(n - 1)}{\alpha \cdot \frac{n(n-1)}{2} + n(n-1)} &\leq \frac{-1(n - 1) + 2n(n - 1)}{\frac{n(n-1)}{2} + n(n-1)} \\ &= \frac{(n-1)(-1 + 2n)}{(n-1)(\frac{n}{2} + n} \\ &= \frac{2n - 1}{\frac32 n} \\ &= \frac{4n - 2}{3n} \\ &\leq \frac43 \end{split}\]
\[\tag*{$\blacksquare$}\]
4 Upper Bound on PoA
Se \(\alpha < 1\), il grafo completo è l'unica rete stabile. Infatti, se \(G(S)\) non genera un grafo completo, allora esistono due nodi \(u, v \in V\) che non sono connessi direttamente, e quindi al giocatore \(u\) conviene pagare l'arco \((u, v)\) in quanto spende \(\alpha\) e risparmia \(1\). Dato poi che per \(\alpha < 1\) il grafo completo è anche ottimo, abbiamo che in questo caso il PoA è \(1\).
Per analizzare il caso \(\alpha \geq 1\) introduciamo qualche definizione utile:
Def. 1: Il diametro di un grafo \(G\) è la massima distanza tra due nodi del grafo.
Def. 2: Un arco \(e\) è detto cut edge di un grafo \(G = (V, E)\) se il grafo
\[G - e := (V, E \ \{e\})\]
è disconnesso.
Seguono quindi dei risultati tecnici.
4.1 Diametro Rete Stabile
Vale il seguente lemma.
Lemma 1: Il diametro di una qualsiasi rete stabile è al più \(2 \sqrt{\alpha} + 1\).
dim: Sia \(G\) una rete stabile, prendiamo due qualsiasi nodi \(u, v \in V\) e consideriamo l'intero \(k\) tale che
\[2k \leq \text{dist}_{G}(u, v) \leq 2k + 1\]
per qualche \(k \in \mathbb{N}\). Graficamente,
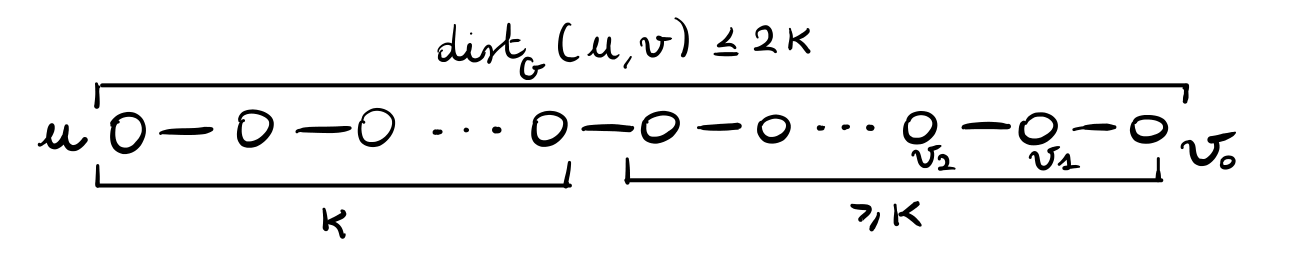
Proviamo a capire come cambierebbe il costo di \(u\) se quest'ultimo decidesse di comprare l'arco \((u, v)\):
Il nodo \(v_0\) passerebbe da una distanza \(\geq 2k\) ad una di \(1\), con un risparmio \(\geq 2k - 1\).
Il nodo \(v_1\) passerebbe da una distanza \(\geq 2k - 1\) ad una di \(2\), con un risparmio \(\geq 2k - 2\).
...
Il nodo \(v_{k-1}\) passerebbe da una distanza \(\geq k + 1\) ad una di \(k\), con un risparmio \(\geq 1\).
Il risparmio complessivo è quindi maggiore o uguale di
\[\sum_{i = 0}^{k - 1} (2i + 1) = k^2\]
Dato che per ipotesi \(G\) è una rete stabile, abbiamo che il costo di comprare l'arco \((u, v)\), che è \(\alpha\), deve essere maggiore del risparmio complessivo. In formula,
\[\alpha \geq \text{ risparmio complesisvo} \geq k^2 \iff k \leq \sqrt{\alpha}\]
Ma allora,
\[\text{dist}_G(u, v) \leq 2k + 1 \leq 2 \sqrt{\alpha} + 1\]
\[\tag*{$\blacksquare$}\]
4.2 Reti Stabili e Non-Cut Edges
Andiamo adesso a limitare il numero di non-cut edges che vengono comprati da un nodo in una rete stabile. Seguono due proposizioni.
Proposizione 1: Sia \(G\) una rete con diametro \(d\) e sia \(e = (u, v)\) un non-cut edge. Allora in \(G - e\) ciascun nodo \(w\) incrementa la propria distanza da \(u\) di al più \(2d\).
dim: Consideriamo il seguente BFS tree radicato in \(u\).
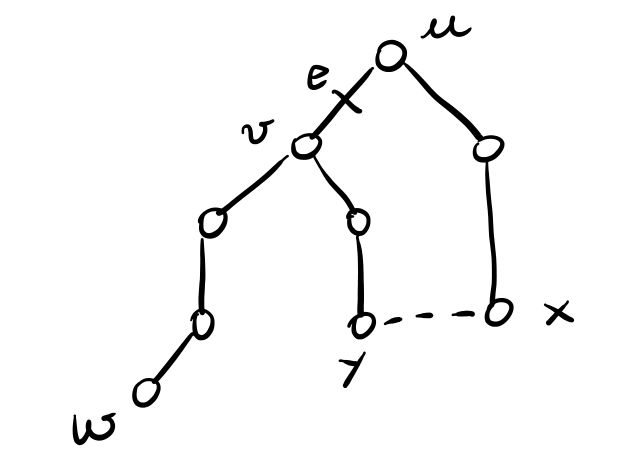
Dato che l'arco \((u, v)\) non è un cut-edge, deve esistere un arco \((x, y)\) che attraversa il taglio nel BFS tree indotto dalla rimozione dell'arco \((u, v)\). Ma allora,
\[\begin{split} d_{G - e}(u, w) &\leq d_G(u, x) + 1 + d_G(y, v) + d_G(v, w) \\ &\leq d + 1 + d + d_G(u, w) - 1 \\ &\leq d_G(u, w) + 2d \\ \end{split}\]
e quindi
\[d_{G - e}(u, w) \leq d_G(u, w) + 2d\]
\[\tag*{$\blacksquare$}\]
Proposizione 2: Sia \(G\) una rete stabile e sia \(F\) l'insieme dei non-cut edges comprati da un nodo \(u\). Allora
\[|F| \leq \frac{(n-1) 2d }{\alpha}\]
dim: Consideriamo il BFS tree con radice su \(u\), e dividiamolo in parti come segue
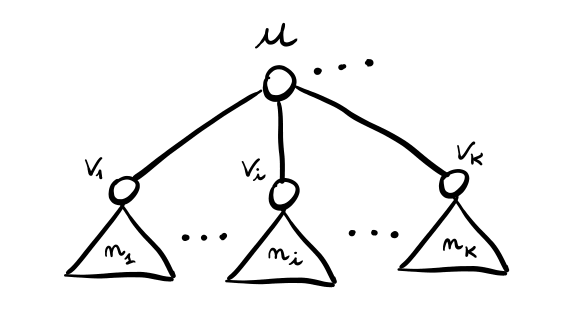
dove \(k := |F|\), mentre \(n_i\) è il numero dei nodi nel sottoalbero radicato in \(V_i\).
Se \(u\) rimuove l'arco \((u, v_i)\), risparmia \(\alpha\), e utilizzando la proposizione precedente sappiamo che la sua distanza dai nodi contenuti nel sottoalbero radicato in \(V_i\) aumenta al più di \(2d\) per ogni nodo. L'incremento totale nel sottoalbero radicato in \(V_i\) è quindi \(2dn_i\).
La rete però è stabile, quindi \(\alpha \leq 2dn_i\). Iterando il ragionamento per \(i = 1, ..., k\) e sommando tutto otteniamo
\[k \alpha \leq \sum_{i = 1}^k 2d n_i \leq 2d (n-1)\]
e quindi
\[k = |F| \leq \frac{2d(n-1)}{\alpha}\]
\[\tag*{$\blacksquare$}\]
4.3 Costo Sociale di una Rete Stabile
Vale il seguente lemma
Lemma 2: Il costo sociale di una qualsiasi rete stabile \(G = (V, E)\) con diametro \(d\) è al più \(O(d)\) volte il costo sociale ottimo.
dim: Notiamo che in qualsiasi soluzione stabile, in totale abbiamo almeno \(n-1\) archi. Nel caso migliore poi ogni coppia di \(n\) nodi si trova a distanza \(1\). Troviamo quindi il seguente lower bound
\[OPT \geq \alpha (n-1) + n (n-1)\]
Il costo sociale invece è dato da
\[SC(G) = \sum_{u, v \in V} d_G(u, v) + \alpha \cdot |E|\]
Notiamo ora che
\[\sum_{u, v \in V} d_G(u, v) \leq d \cdot n (n - 1) \leq d \cdot OPT\]
\[\begin{split}\alpha \cdot |E| &= \alpha \cdot |E_{\text{cut}}| + \alpha \cdot |E_{\text{non-cut}}| \\ &\leq \alpha (n-1) + \alpha \cdot \frac{n(n-1)2d}{\alpha} \\ &\leq 2d \cdot OPT\end{split}\]
Dove il secondo punto è ottenuto utilizzando la proposizione 2 più il fatto che banalmente un grafo \(G\) può avere al più \(n - 1\) cut edges. Mettendo tutto assieme troviamo
\[SC(G) = \sum_{u, v \in V} d_G(u, v) + \alpha \cdot |E| \leq d \cdot OPT + 2d \cdot OPT = 3d \cdot OPT\]
\[\tag*{$\blacksquare$}\]
4.4 Risultato Finale
Utilizzando il lemma 1 e il lemma 2 siamo in grado di dimostrare il seguente teorema, che pone un upper bound al PoA.
Teorema: Il PoA per il LCG con parametro \(\alpha\) è al più \(O(\sqrt{\alpha})\).
dim: Sia \(G\) una qualsiasi rete stabile. Dal lemma 1 segue che il diametro di \(G\) è \(O(\sqrt{\alpha})\). Dal lemma 2 invece segue che il costo sociale di \(G\) è \(O(\sqrt{\alpha})\) volte quello ottimo. Ma allora per definizione
\[\text{PoA} = O(\sqrt{\alpha})\]
\[\tag*{$\blacksquare$}\]
5 La Best Reponse è NP-Hard
Concludiamo dimostrando un risultato di impossibilità.
Teorema: Il calcolo della best response per il LCG è un problema NP-Hard.
L'idea è di proporre una riduzione dal problema Dominating Set (DS), definito come segue:
Input: Un grafo \(G = (V, E)\).
Solutions: Un sottoinsieme di vertici \(U \subseteq V\) che "ricopre" tutto il grafo, ovvero tale che per ogni nodo \(v \in V \setminus U\) esiste un nodo \(u \in U\) tale che \((u, v) \in E\).
Goal: Minimizzare la cardinalità del sottoinsieme \(U\).
Procediamo quindi con la riduzione.
dim: Sia \(1 < \alpha < 2\) e consideriamo una istanza \(I\) del problema DS.
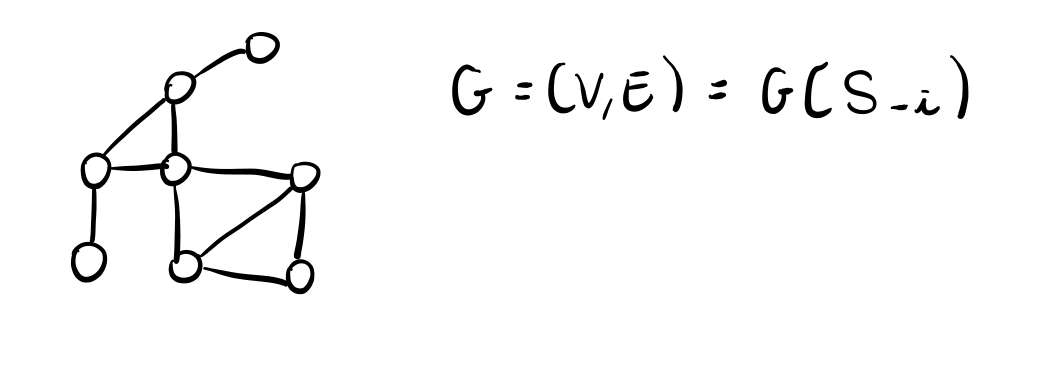
Mettiamoci nei panni del giocatore \(i\) e consideriamo il grafo dell'istanza \(I\) come se fosse il grafo costruito dagli altri giocatori. Dimostriamo quindi che il giocatore \(i\) ha una strategie di costo \(\leq \alpha \cdot k + 2n - k\) se e solo se esiste un dominating set di size \(\leq k\).
\((\Leftarrow)\): Dato un DS \(U\) di size \(|U| \leq k\), se il giocatore \(i\) si connette a tutti i nodi del dominating set paga al più
\[\underbrace{\alpha \cdot k}_{\text{costo per archi}} + \underbrace{2(n-k) + k}_{\text{costo per distanza}} = \alpha k + 2n - k\]
\[\tag*{$\checkmark$}\]
\((\Rightarrow)\): Sia \(S_i\) una strategia di costo \(\leq \alpha k + 2n - k\). Se in \(G(S_i)\) esiste un nodo \(v\) che si trova ad una distanza \(\geq 3\) dal giocatore \(i\) (nodo \(x\)), allora modifichiamo la strategia del giocatore \(i\) aggiungendo l'arco \((x, v)\) ad \(S_i\). Dato che \(\alpha < 2\) questa modifica non andrà ad aumentare il costo per \(i\). Alla fine abbiamo che in \(G(S_i)\) tutti i nodi distano da \(i\) o di \(1\) o di \(2\).
Sia quindi \(U\) l'insieme dei nodi che distano \(1\) da \(x\). Allora \(U\) è un dominating set, e inoltre
\[\text{COST}_i(S) = \alpha \cdot |U| + 2n - |U| \leq \alpha \cdot k + 2n - k \iff |U| \leq k\]
\[\tag*{$\checkmark$}\]
Avendo dimostrato entrambi i lati, abbiamo concluso la dimostrazione.
\[\tag*{$\blacksquare$}\]