AGT - 05 - Algorithmic Mechanism Design II
Lecture Info
Data:
Sito corso: AGT_2018
Slides: 05 - AMD II
Introduzione: In questa lezione continuiamo la trattazione del mechanism design, definendo i problemi ad un parametro ed introducendo un meccanismo truthful per risolverli.
1 Shortest Path (with Selfish-Edges)
Andiamo a trattare il problema del calcolo del cammino minimo tra due nodi in un grafo in cui gli archi sono controllati da agenti egoistici. Per fare questo sarà necessario progettare un meccanismo truthful che incentivi i vari agenti a dire la verità.
Intuitivamente il problema è così descritto:
Abbiamo un grafo \(G = (V, E)\) in cui ogni arco \(e \in E\) è un agente egoistico.
Sono poi specificati due particolari nodi del grafo \(s, t \in V\).
Il tipo di un agente è il costo di utilizzo dell'arco. Questa informazione è mantenuta privata dall'agente, e non necessariamente viene riportata dall'agente.
La valutazione di un agente è uguale al valore del tipo.
La social-choice function è un vero cammino minimo in \(G = (V, E, \text{tipi})\) tra \(s\) e \(t\).
Più formalmente abbiamo:
Le soluzioni ammissibili, ovvero i possibili outcomes del gioco, è l'insieme \(\mathcal{F}\) dei cammini in \(G\) da \(s\) a \(t\).
Il tipo dell'agente \(e\) è il valore \(\tau_e\) che rappresenta il peso dell'arco \(e\) nel grafo \(G\). Il valore riportato dall'agente è invece \(r_e\). In generale potrebbe succedere che \(r_e \neq \tau_e\).
Dato un outcome \(P \in \mathcal{F}\), la valutazione dell'agente \(e\) nel cammino \(P\) è data da
\[V_e(\tau_e, P) = \begin{cases} \tau_e \,\,&,\,\, e \in P \\ 0 \,\,&,\,\, \text{ altrimenti } \\ \end{cases}\]
Dato il vettore dei tipi \(\tau\), la social-choice function calcola la shortest path in \(G = (V, E, \tau)\), tra i due nodi specificati nell'input \(s\) e \(t\).
1.1 Designing a Mechanism
Calcolare la shorest path significa calcolare il cammino di costo minimo. Dato un cammino \(P\) il suo costo è la somma dei pesi degli archi presenti nel cammino. In formula,
\[\sum_{e \in P} \tau_e = \sum_{e \in E} v_e(\tau_e, P)\]
Questo significa che la social-choice function per il nostro obiettivo è proprio la seguente
\[f(\tau) = \underset{P \in \mathcal{F}}{\arg\min} \sum\limits_{e \in E} v_e(\tau_e, P)\]
In altre parole il problema che vogliamo risolvere è un problema utilitario. Per progettare un meccanismo truthful possiamo quindi utilizzare i meccanismi VCG introdotti nella scorsa lezione. Ricordiamo che \(M = \langle g(r), p(x) \rangle\) è un meccanismo VCG se ha la seguente forma
\(g(r) := \underset{x \in \mathcal{F}}{\arg\min} \sum\limits_j v_j(r_j, x)\)
\(p_i := \sum_{j \neq i} v_j(r_j, g(r_{-i})) - \sum_{j \neq i} v_j(r_j, g(r))\)
Nel nostro caso particolare troviamo che
L'algoritmo \(g(r)\) calcola un cammino minimo \(P_G(s, t)\) nel grafo \(G = (V, E, r)\) pesato con i tipi ripotati.
Fissato un outcome \(g(r) = P_G(s, t)\), l'agente \(e \in E\) viene pagato nel seguente modo
\[p_e(P_G(s, t)) = \sum_{j \neq e} v_j(r_j, g(r_{-e})) - \sum_{j \neq e} v_j(r_j, P_G(s, t))\]
ovvero,
\[p_e(P_G(s, t)) = \begin{cases} d_{G - e}(s, t) - (d_G(s, t) - r_e) \,\,&,\,\, e \in P_G(s, t) \\ 0 \,\,&,\,\, \text{ altrimenti } \\ \end{cases}\]
Per il calcolo dei pagamenti per ogni \(e \in P_G(s, t)\) dobbiamo quindi calcolare \(P_{G - e}(s, t)\) detto anche il cammino minimo di rimpiazzo nel grafo \(G - e := (V, E \setminus \{e\}, r_{-e})\) tra \(s\) e \(t\).
Esempio: Consideriamo il seguente grafo
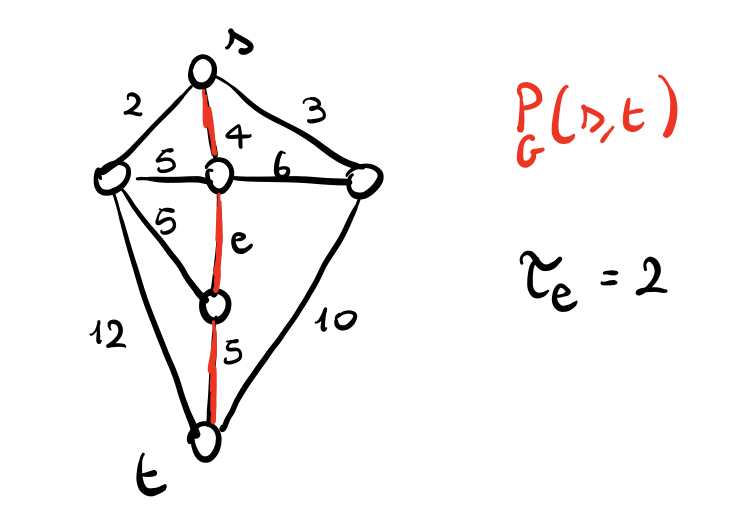
Per calcolare il pagamento di \(e \in P_G(s, t)\) dobbiamo prima calcolare il cammino di rimpiazzo per \(e\)
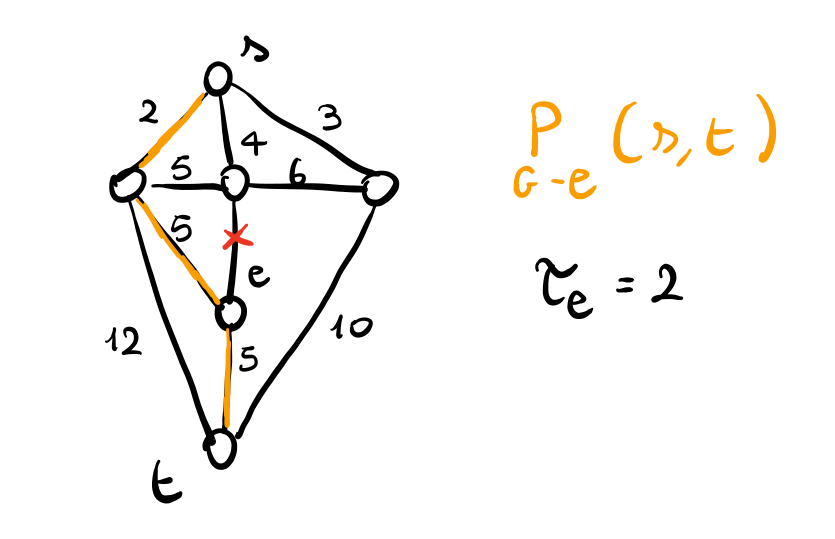
Alla fine troviamo
\[P_e = d_{G - e}(s, t) - (d_G(s, t) - r_e) = 12 - (11 - 2) = 3\]
1.2 Complexity Analysis
Sia \(n := |V|\), \(m := |E|\), e indichiamo con \(d_G(s, t)\) la distanza in \(G\) da \(s\) a \(t\).
Notiamo che i nodi \(s\) e \(t\) sono 2-edge connessi, ovvero esistono in \(G\) almeno \(2\) cammini tra \(s\) e \(t\) che sono disgiunti sugli archi. Se così non fosse infatti ci sarebbe almeno un arco in \(P_G(s, t)\) che è un ponte, e quindi che se rimosso spezza \(G\) in due componenti \(C_1\) e \(C_2\), con \(s \in C_1\) e \(t \in C_2\). In questo caso abbiamo che \(d_{G - e}(s, t) = + \infty\). In altre parole, il possessore del pointe può chiedere qualsiasi cifra. Restringendoci dunque a tutte le instanze in cui \(s\) e \(t\) sono 2-edge connessi, abbiamo che per ogni arco \(e \in P_G(s, t)\) rimosso esiste almeno un cammino alternativo in \(G - e\) che collega \(s\) a \(t\).
Per calcolare i pagamenti possiamo quindi applicare, per ogni arco \(e \in P_G(s, t)\), l'algoritmo di Dijkstra al grafo \(G - e\). La complessità di questo approccio è
\[\underbrace{O(n)}_{\text{# archi in } P_G(s, t)} \cdot \underbrace{O(m + n \log{n})}_{\text{Calcolo $P_{G-e}(s, t)$ fissato $e \in P_G(s, t)$}} = O(nm + n^2 \log {n})\]
In realtà vale un risultato ancora migliore, dimostrato da Malik, Mitta, Gutpa nell'articolo "The \(k\) most vital arcs in the shortest path problem", 1989, che risolve il problema in \(O(m + m \log n)\).
1.3 Exercise
Stesso problema ma un agente può controllare più archi. In particolare abbiamo \(k \leq m := |E|\) agenti, ciascuno dei quali controlla un sottoinsieme di archi \(E_i \subseteq E\). L'agente \(a_i\) dichiara \(r:i E_i \to \mathbb{R}^+\), dove \(r_i(e)\) è il peso dichiarato dall'agente \(i\) per l'arco \(e \in E_i\), mentre il vero costo dell'arco è \(\tau_i(e)\).
Dato un outcome \(P \in \mathcal{F}\), la valutazione dell'agente \(i\) è
\[v_i(r_i, P) = \sum_{e \in E_i \cap P} r_i(e)\]
Notiamo che nuovamente il problema è un problema utilitario. Per risolverlo possiamo quindi utilizzare un meccanismo VCG \(M = \langle g(r), p(x) \rangle\) in cui l'algoritmo \(g(r)\) calcola il cammino minimo sul grafo pesato con i valori riportati dagli agenti, mentre il pagamento per l'agente \(i\) è dato da
\[\begin{split} p_i(P_G(s, t)) &= \sum_{j \neq i} v_j(r_j, P_{G \setminus E_i}(s, t)) - \sum_{j \neq i} v_j(r_j, P_G(s, t)) \\ &= d_{G - E_i}(s, t) - \Big( d_G(s, t) - \sum_{e \in E_i \cap P} r_i(e) \Big) \\ \end{split}\]
\[\tag*{$\checkmark$}\]
2 One-Parameter (OP) Problems
Segue un'altra classe di problemi per cui esistono dei meccanismi truthful.
Def. Un problema è detto one parameter (OP) se
L'informazione posseduta da ogni singolo agente \(a_i\) è un singolo parametro \(t_i \in \mathbb{R}\).
La valutazione dell'agente \(a_i\) nell'outcome \(o \in \mathcal{F}\) ha la forma
\[v_i(t_i, o) = t_i \cdot w_i(o)\]
dove \(w_i(o)\) è il carico di lavoro per \(a_i\) nell'outcome \(o\).
A differenza dei meccanismi VCG, che non vincolano i tipi e le valutazioni, ma che possono essere utilizzati solo per problemi utilitari, i meccanismi OP invece non vincolano la funzione sociale ma richiedono che i tipi siano a singolo parametro e vincolano la struttura delle funzioni di valutazione.
2.1 \(M\) Truthful \(\Rightarrow\) \(g(\cdot)\) Monotone
Per introdurre un meccanismo da poter utilizzare per i problemi one-parameter, è utile introdurre la seguente definizione, che ci permetterà di identificare una condizione necessaria affinché un meccanismo \(M\) per un problema OP sia truthful.
Def. Un algoritmo \(g(\cdot)\) per un problema OP di minimizzazione è monotono se per ogni agente \(a_i\), il carico di lavoro \(w_i(g(r_{-i}, r_i))\) è non crescente rispetto a \(r_i\) per tutti gli \(r_{-i} = (r_1, \ldots, r_{i-1}, r_{i+1}, \ldots, r_N)\).
Vale quindi il seguente.
Teorema 1 (Mayerson '81): Una condizione necessaria affinché un meccanismo \(M = \langle g(r), p(x) \rangle\) per un problema OP sia truthful è che \(g(r)\) sia monotono.
dim. Supponiamo per assurdo che \(g(\cdot)\) non sia monotono. Allora esiste un agente \(a_i\) e un vettore \(r_{-i}\) tale che la funzione \(w_i(g(r_{-i}, r_{i}))\) è non "non crescente" rispetto a \(r_i\). Graficamente,
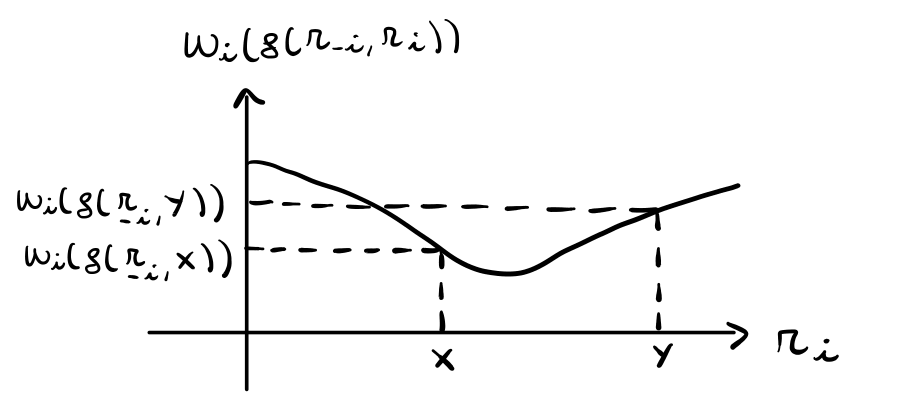
Consideriamo adesso i seguenti quattro casi:
\(t_i = x, r_i = x \implies v_i(t_i, o) = x \cdot w_i(g(r_{-i}, x))\)
\(t_i = y, r_i = y \implies v_i(t_i, o) = y \cdot w_i(g(r_{-i}, y))\)
\(t_i = x, r_i = y \implies v_i(t_i, o) = x \cdot w_i(g(r_{-i}, y)) \implies a_i \text{ aumenta il suo costo di } A\)
\(t_i = y, r_i = x \implies v_i(t_i, o) = y \cdot w_i(g(r_{-i}, x)) \implies a_i \text{ ha un risparmio di } A +k\)
Dove \(A\) e \(k\) sono le seguenti aree
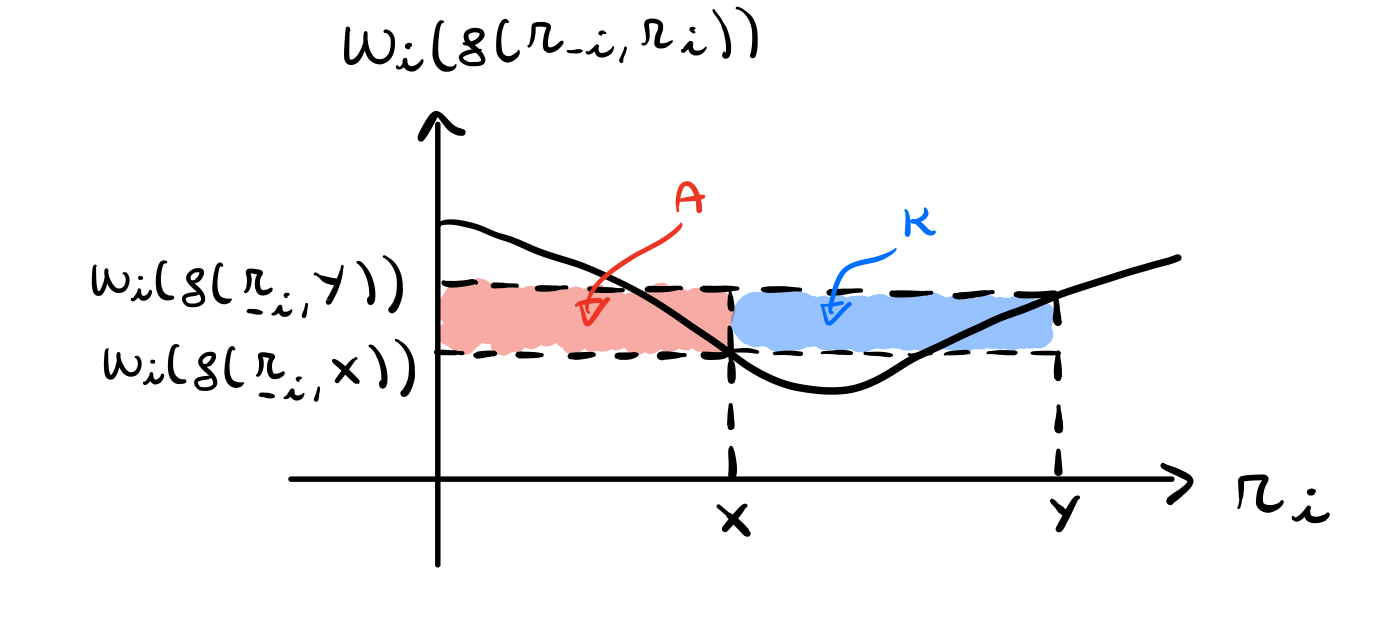
Sia quindi \(\Delta p = p_i(g(r_{-i}, y)) - p_i(g(r_{-i}, x))\). Per avere un meccanismo truthful dobbiamo sicuramente avere
\((\Delta p \leq A)\). Se così non fosse infatti nel caso in cui \(t_i = x\) al giocatore \(a_i\) converrebbe mentire e riportare \(r_i = y\). Così facendo infatti l'aumento del pagamento supererebbe quello del costo aggiuntivo, e il giocatore avrebbe una utility finale \(> 0\) mentendo.
\((\Delta p \geq A + k)\). Se così non fosse, nel caso in cui \(t_i = y\) al giocatore \(a_i\) converebbe riportare \(r_i = x\), in quanto l'incremento del pagamento da \(x\) a \(y\) non supera il risparmio nel riportare \(x\) al posto di \(y\). Nuovamente, il giocatore avrebbe una utility finale \(> 0\) mentendo.
Ma \(k > 0\), e quindi non possono valere queste due condizioni assieme.
\[\tag*{$\Huge\unicode{x21af}$}\]
2.2 OP (Truthful) Mechanism
Dato un problema OP, un meccanismo che possiamo utilizzare è \(M = \langle g(r), p(x) \rangle\), dove l'unica restrizione che imponiamo sull'algoritmo \(g(r)\) è che deve essere monotono, e fissato un outcome \(x \in \mathcal{F}\), il pagamento da assegnare all'agente \(i\) è il seguente
\[p_i(r) := h_i(r_{-i}) + r_i \cdot w_i(x) + \int\limits_{0}^{r_i} w_i(g(r_{-i}, z)) \,\, dz\]
Osserviamo come questo meccanismo è truthful. Vale infatti il seguente risultato.
Teorema 2 (Mayerson '81): Un meccanismo OP per un problema OP è truthful.
dim. L'idea è di mostrare che se \(a_i\) mente la sua utilità non può fare altro che diminuire. A tale fine fissiamo le dichiarazioni degli altri agenti \(r_{-i}\). Per come abbiamo definito il meccanismo, il pagamento fornito da \(a_i\) quando dichiara \(r_i\) è dato da
\[p_i(g(r)) = h_i(r_{-i}) + r_i \cdot w_i(g(r)) - \int\limits_{0}^{r_i} w_i(g(r_{-i}, z)) \,\, dz\]
Dato che \(h_i(r_{-i})\) non dipende dalla scelta del giocatore \(i\), posso ignorare questo fattore ponendolo a \(0\), \(h_i(r_{-i}) = 0\).
Cominciamo quindi considerando l'utilità di \(a_i\) quando dice la verità.
\[\begin{split} u_i(t_i, g(r_{-i}, t_i)) &= p_i(g(r_{-i}, t_i)) - v_i(t_i, g(r_{-i}, t_i)) \\ &= \Big(t_i w_i(g(r_{-i}, t_i)) - \int\limits_{0}^{t_i} w_i(g(r_{-i}, z)) \,\, dz \Big) - t_i \cdot w_i(g(r_{-i}, t_i)) \\ &= - \int\limits_{0}^{t_i} w_i(g(r_{-i}, z)) \,\, dz \\ \end{split}\]
Graficamente,
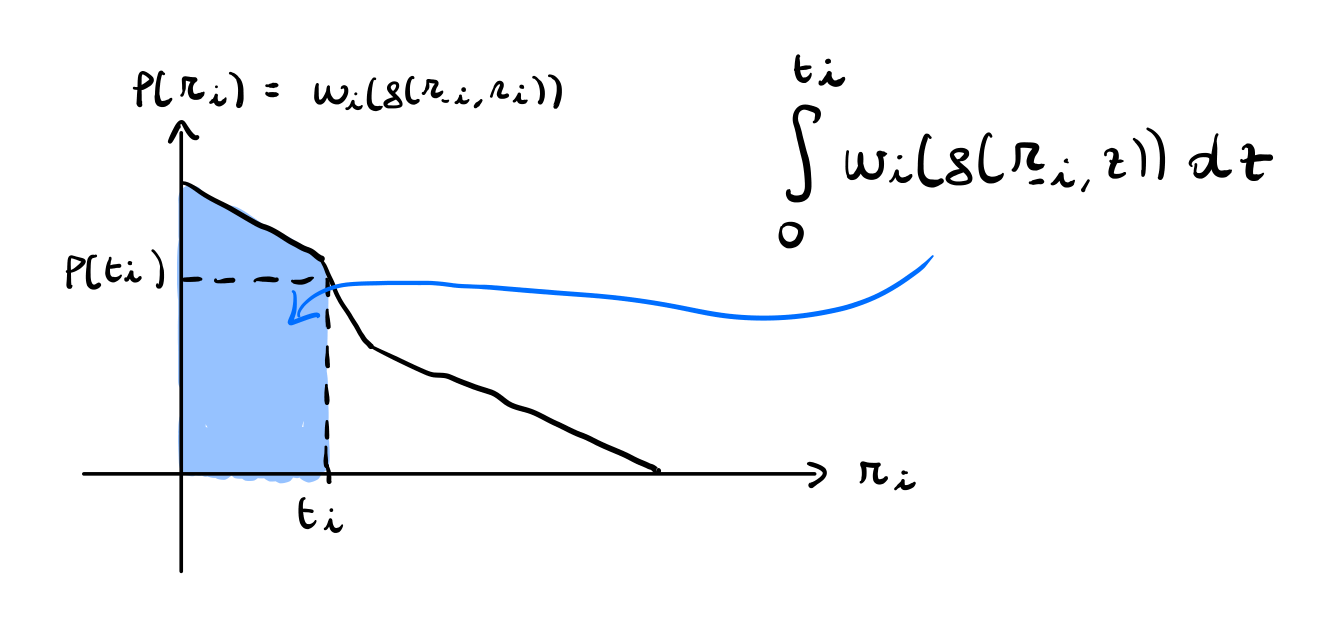
Se invece \(a_i\) mente, allora dichiara un valore \(r_i\) diverso da \(t_i\). la valutazione diventa
\[C = t_i \cdot w_i(g(r_{-i}, x))\]
il pagamento diventa
\[P = x \cdot w_i(g(r_{-i}, x)) - \int\limits_0^x w_i(g(r_{-i}, z)) \,\, dz \]
e l'utilità diventa
\[\begin{split} U &= P - C \\ &= x \cdot w_i(g(r_{-i}, x)) - \int\limits_0^x w_i(g(r_{-i}, z)) \,\, dz - t_i \cdot w_i(g(r_{-i}, x)) \\ &= (x - t_i) \cdot w_i(g(r_{-i}, x)) - \int\limits_0^x w_i(g(r_{-i}, z)) \,\, dz \\ \end{split}\]
Andiamo quindi ad analizzare i due possibili casi in cui ci possiamo trovare.
(\(a_i\) dichiara \(r_i = x > t_i\)). In questo caso troviamo la seguente situazione
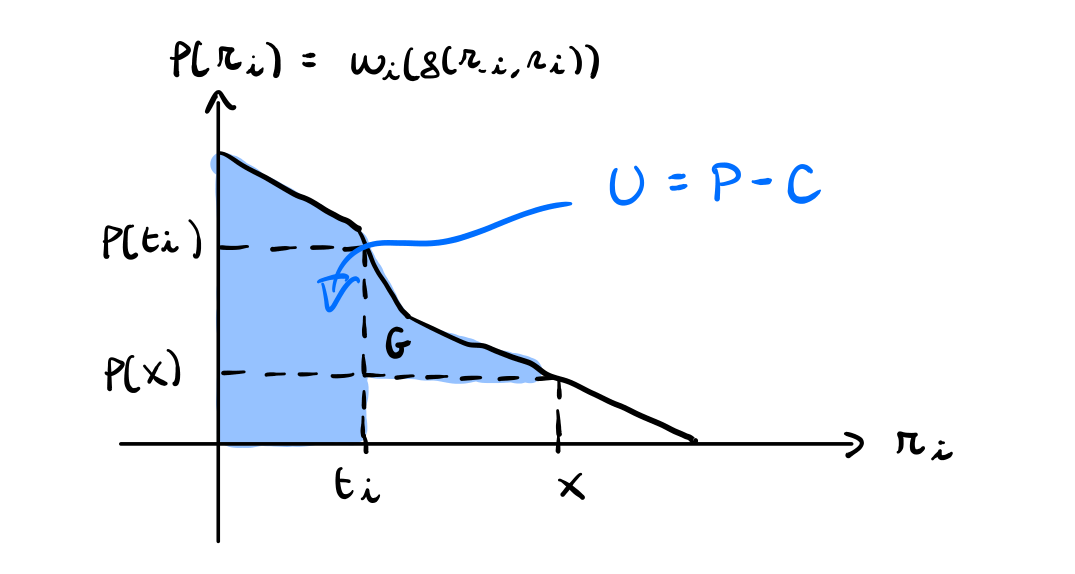
Confrontando questo grafico con quello precedente, notiamo che questa volta prendiamo in considerazione anche l'aria aggiuntiva \(G\). Dato che queste aree vengono sottratte all'utilità finale, concludiamo che \(a_i\) sta perdendo \(G\) se mente dicendo \(x > t_i\).
(\(a_i\) dichiara \(r_i = x < t_i\)). In questo caso troviamo la seguente situazione
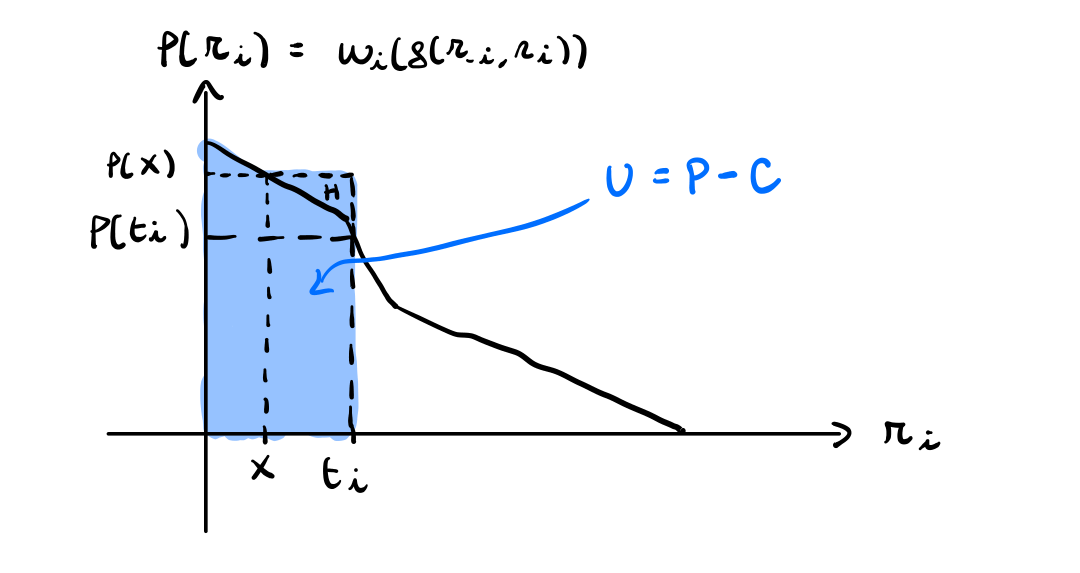
Nuovamente, abbiamo più area negativa da sottrarre. In particolare \(a_i\) perde l'area \(H\), e dunque anche in questo caso ad \(a_i\) non conviene mentire.
In entrambi i casi dunque all'agente \(a_i\) non conviene mentire.
\[\tag*{$\blacksquare$}\]
2.2.1 How to Define \(h_i(r_{-i})\)
Per garantire la volontaria partecipazione (VP) un meccanismo deve garantire una utility \(> 0\) a tutti gli agenti che dicono la verità. A tale fine scegliamo di definire \(h_i(r_{-i})\) nel seguente modo
\[h_i(r_{-i}) = \int\limits_0^{+\infty} w_i(g(r_{-i}, z)) \,\, dz\]
Così facendo il pagamento diventa
\[p_i(x) = r_i \cdot w_i(x) + \int\limits_{r_i}^{+\infty} w_i(g(r_{-i}, z)) \,\, dz\]
e l'utilità dell'agente \(a_i\) quando dice la verità è
\[u_i(t_i, g(r)) = \int\limits_{t_i}^{+\infty} w_i(g(r_{-i}, z)) \,\, dz \geq 0\]
3 Shortest-Paths Tree (with Selfish-Edges)
Consideriamo la versione "egoistica" del problema di trovare l'albero dei cammini minimi. Abbiamo una sorgente \(s \in V\) che vuole inviare un messaggio ai restanti nodi in \(V \setminus \{s\}\). Per ogni arco \(e \in E\) abbiamo un agente, il cui dato privato è il tempo di attraversamento del messaggio nell'arco. L'obiettivo è quello di minimizzare il tempo di consegna complessivo.
Formalizzando,
L'insieme dei possibili outcomes \(\mathcal{F}\) è l'insieme degli alberi ricoprenti \(V\) radicati in \(s\).
Fissato un vettore dei tipi \(t\), la social-choice function è definita come segue
\[f(t) := \underset{T \in \mathcal{F}}{\arg\min} \sum_{v \in V} d_T(s, v) = \underset{T \in \mathcal{F}}{\arg\min} \sum_{e \in E(T)} t_e \cdot ||e||\]
Dove con \(||e||\) stiamo indicando la molteplicità dell'arco \(e\) nella soluzione \(T\), ovvero il numero di cammini in \(T\) a cui \(e\) appartiene.
Osserviamo come la valutazione del player \(a_e\) fissato un outcome \(T \in \mathcal{F}\) dipenda da come i messaggi vengono trasmessi nella rete. Supponendo di utilizzare un protocollo multicast in cui una sola copia del messaggio viene spedita su ogni arco, per poi essere eventualmente duplicata dai nodi riceventi, troviamo una situazione del genere
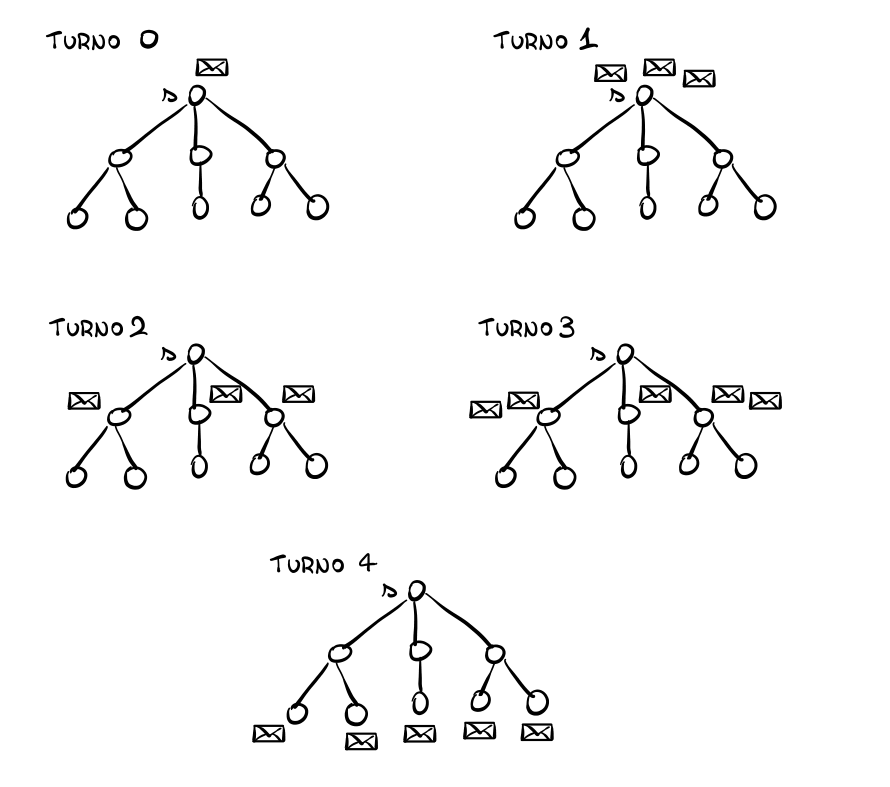
Fissato un outcome \(T \in \mathcal{F}\), la valutazione del giocatore \(a_e\) è così definita
\[v_e(t_e, T) = \begin{cases} t_e \,\,&,\,\, e \in E(T) \\ 0 \,\,&,\,\, \text{ altrimenti } \\ \end{cases}\]
Da questo segue che il problema non è un problema utilitario, in quanto
\[f(t) \neq \underset{T \in \mathcal{F}}{\arg\min} \sum_{e \in E(T)} v_e(t_e, T)\]
Il problema è invece un problema one-parameter, in quanto il tipo di ogni agente \(a_e\) è un singolo parametro \(t_e \in \mathbb{R}\), mentre la valutazione sotto ipotesi di trasferimento multicast è data da
\[v_e(t_e, T) = t_e \cdot w_e(T)\]
con
\[w_e(T) = \begin{cases} 1 \,\,&,\,\, e \in E(T) \\ 0, \,\,&,\,\, \text{ altrimenti } \end{cases}\]
3.1 Designing a Mechanism
Un meccanismo possibile è quindi il meccanismo \(M_{\text{SPT}} = \langle g(r), p(x) \rangle\) con
\(g(r)\) che calcola uno shortest-path-tree (SPT) \(S_G(s)\) del grafo con i pesi riportati \(G = (V, E, r)\) utilizzando l'algoritmo di Dijkstra.
Il pagamento dell'arco \(e \in E\) è invece dato da
\[p_e(x) = r_e \cdot w_e(x) + \int\limits_{r_e}^{+ \infty} w_e(g(r_{-e}, z)) \,\, dz\]
Notiamo che tale meccanismo è truthful in quanto l'algoritmo di Dijkstra è monotono. Fissato \(r_{-e}\) il carico di lavoro per un agente \(a_e\) ha infatti sempre la seguente forma
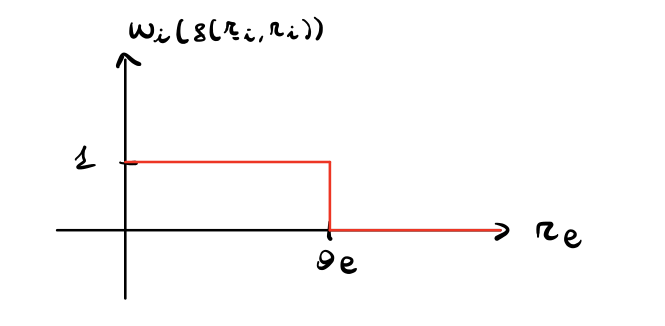
Il valore \(\theta_e\) in cui il carico passa da \(1\) a \(0\) è chiamato soglia, ed è importante nel calcolo dei pagamenti. Abbiamo infatti che
Se \(e\) non fa parte della soluzione, ovvero \(e \not \in E(T)\), allora
\[p_e = r_e \cdot w_e(g(r)) + \int\limits_{r_e}^{+ \infty} w_e(g(r_{-e}, z)) \,\, dz = 0 + 0 = 0\]
Se \(e\) fa parte della soluzione, ovvero \(e \in E(T)\), allora
\[p_e = r_e \cdot w_e(g(r)) + \int\limits_{r_e}^{+ \infty} w_e(g(r_{-e}, z)) \,\, dz = r_e + (\theta_e - r_e) = \theta_e\]
Sia \(e = (u, v)\) un arco in \(S_G(s)\), con \(u\) più vicino a \(s\) che \(v\), e andiamo a calcolare il valore della soglia \(\theta_e\). Notiamo che \(e\) resta in \(S_G(s)\) fintantoché utilizzo \(e\) per raggiungere \(v\), come mostra il seguente esempio
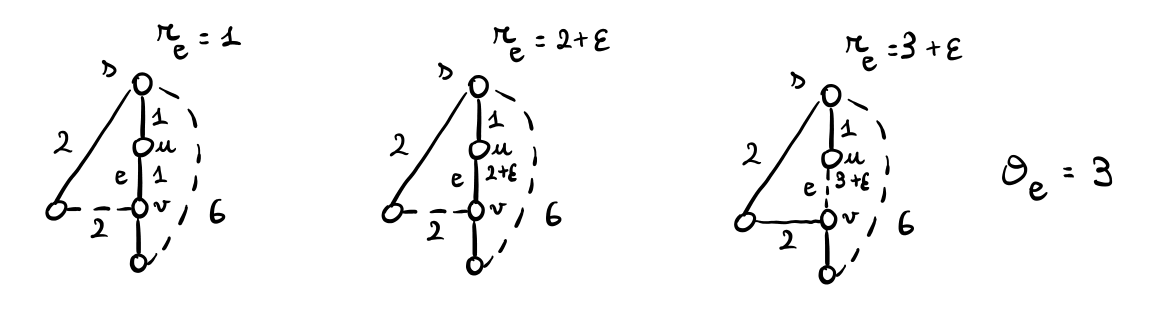
In particolare il momento in cui \(r_e\) è tale che
\[d_G(s, u) + r_e > d_{G - e}(s, v)\]
allora \(e\) non viene più scelto. Dunque il valore soglia per \(e\) è tale che
\[\begin{split} &\,\,\, d_G(s, u) + \theta_e = d_{G - e}(s, v) \\ \iff&\,\,\, \theta_e = d_{G - e}(s, v) - d_G(s, u) \\ \end{split}\]
Mettendo tutto assieme, una soluzione banale per il problema dello SPT non cooperativo consiste nel calcolare \(S_g(s)\) utilizzando Dijkstra sul grafo con i pesi riportati, per poi calcolare \(d_{G - e}(s, v)\) per ogni \(e \in S_g(s)\) sempre utilizzando Dijkstra sul grafo \(G - e\) in modo tale da calcolare il pagamento per \(e\).
3.2 Complexity Analysis
Sia \(n := |V|\), \(m := |E|\). La complessità di questo approccio è
\[\underbrace{O(n)}_{\text{# archi in } S_g(s)} \cdot \underbrace{O(m + n \log{n})}_{\text{Calcolo $d_{G-e}(s, v)$ fissato $e \in S_g(s)$}} = O(nm + n^2 \log {n})\]
Vale poi il seguente teorema.
Teorema: \(M_{\text{SPT}}\) è calcolabile in tempo \(O(m + n \log n)\).
4 Binary Demand Problems
Il problema che abbiamo affrontato in realtà appartiene ad una classe particolare di problemi ad un parametro, anche nota con il nome di binary demand (BD). Un problema BD è caratterizzato dal fatto che
L'informazione privata di ogni agente \(a_i\) è un singolo parametro \(t_i \in \mathbb{R}\).
La valutazione di \(a_i\) ha la forma
\[v_i(t_i, o) = t_i w_i(o)\]
dove \(w_i(o) \in \{0, 1\}\) è il carico di lavoro per \(a_i\) in \(o\). Quando \(w_i(o) = 1\) diremo che l'agente \(a_i\) è stato selezionato nell'outcome \(o\).
Segue una definizione importante.
Def. Un algoritmo \(g(\cdot)\) per un problema BD di minimizzazione è monotono se per ogni agente \(a_i\) e per tutti gli \(r_{-i} = (r_1, *\ldots, r_{i-1}, r_{i+1}, \ldots, r_N)\) la funzione \(w_i(g(r_{-i}, *r_i))\) ha la seguente forma

In questo caso il valore \(\theta_i(r_{-i}) \in \mathbb{R} \cup \{+ \infty\}\) è detto valore di soglia e il pagamento per l'agente \(a_i\) diventa \(p_i(r) = \theta_i(r_{-i})\).
5 Esercizi
Seguono due esercizi.
Single-Item Auction (versione minimizzazione) in cui si vuole allocare il job alla seconda macchina migliore.
SPT (non cooperativo) in cui un agente controlla più di un arco.