AGT - 07 - Stackelberg MST Game
Lecture Info
Data:
Sito corso: AGT_2018
Slides: 07 - Stackelberg MST Game
Introduzione: In questa lezione abbiamo affrontato un problema in particolare chiamato stackelberg MST game, analizzando sia un risultato di NP-Hardness e presentando un semplice algoritmo approssimante.
1 MST Problem
Per ragionare sul problema che affronteremo in questa lezione è utile ripassare brevemente il classico problema del minimo albero ricoprente, in inglese Minimum Spanning Tree Problem.
L'MST problem è così definito:
Input: Un grafo non-diretto e pesato \(G = (V, E, w)\).
Solution: Uno spanning tree di \(G\), ovvero un albero \(T = (V, E)\) con \(F \subseteq E\).
Measure: L'obiettivo è minimizzare il peso totale di \(T\), ovvero
\[\sum_{e \in F} w(e)\]
1.1 Kruskal's Algorithm
Per risolvere questo problema è possibile utilizzare l'algoritmo di Kruskal, che funziona come segue:
Si inizia con un albero vuoto \(T\);
Si procede considerando gli archi di \(G\) in ordine non-decrescente, ovvero dal più piccolo al più grande, e si aggiunge l'arco \(e\) a \(T\) se e solo se l'aggiunta di questo arco non va a creare in \(T\) cicli.
1.1.1 Example
Consideriamo il seguente grafo
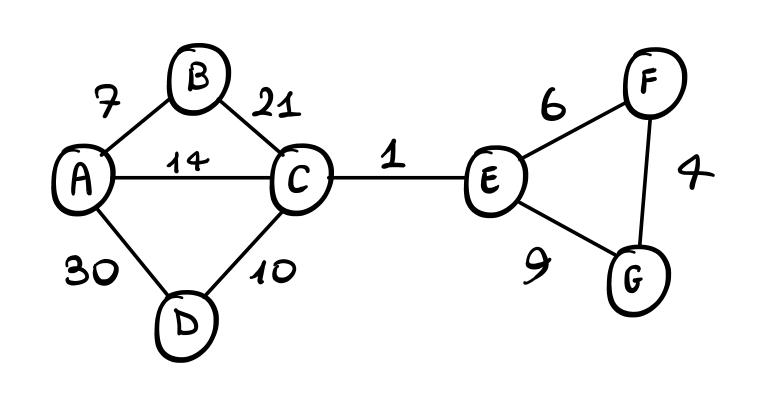
Applicando l'algoritmo di Kruskal otteniamo il seguente risultato
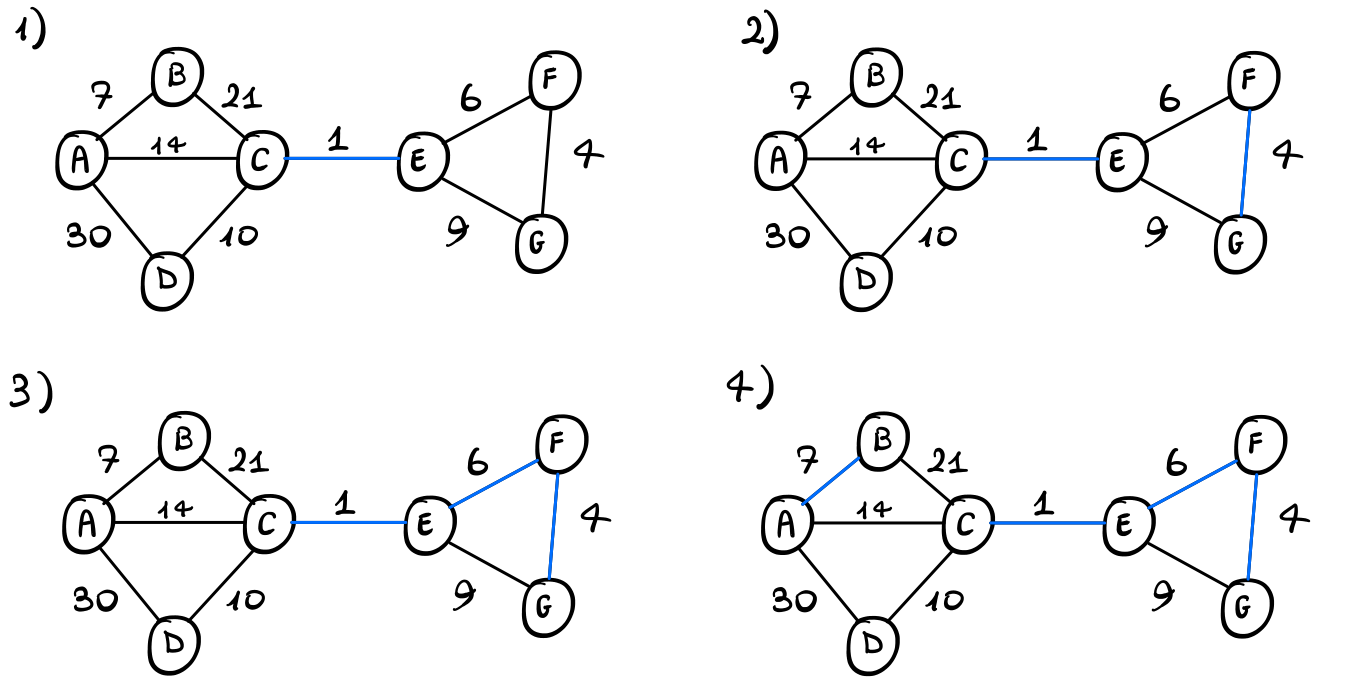
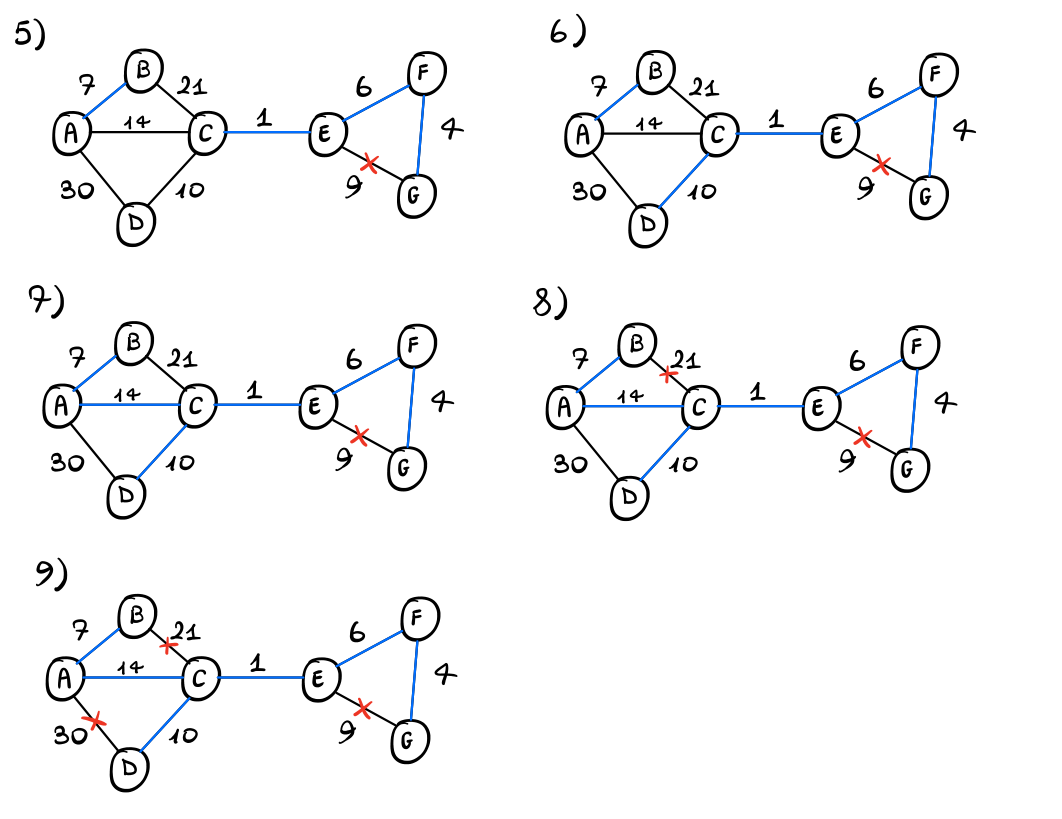
Lo spanning tree costruito alla fine è quindi il seguente
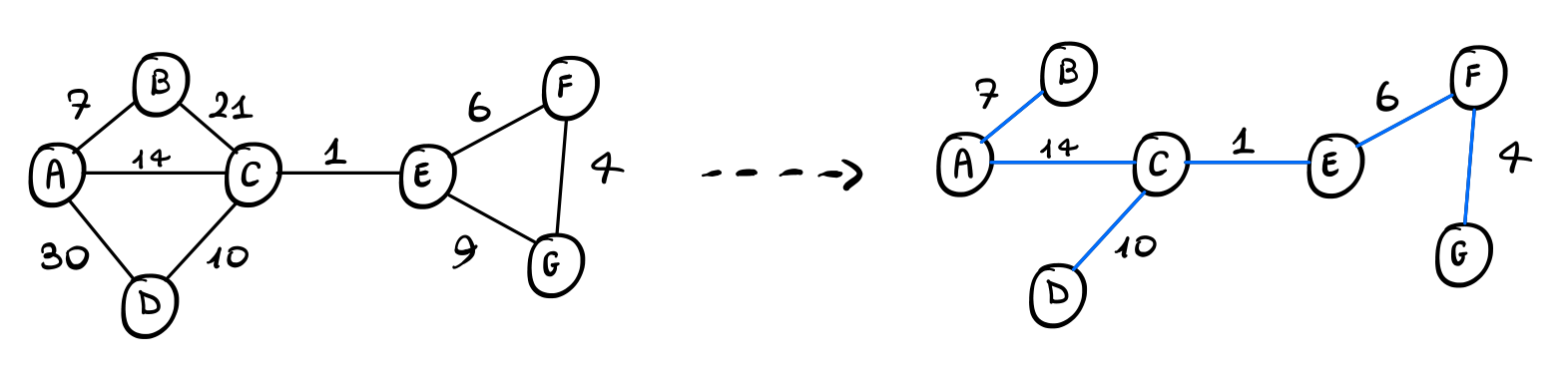
2 Stacklberg MST Game
Lo stackelberg MST game è giocato da due giocatori: un leader e un follower. Il leader si muove per primo, mentre il follower per secondo. Ciascuno dei due players vuole ottimizzare una propria funzione obiettivo, ma il follower ottimizza la propria funzione conoscendo la mossa del leader, mentre il leader è costretto a scegliere la sua mossa anticipando quella del follower. Il nostro obiettivo è trovare una buona strategia per il leader.
Più formalmente:
Abbiamo un grafo \(G = (V, E)\) con \(E = R \cup B\).
Ogni arco \(e \in R\) ha un costo fissato \(c(e) \in \mathbb{R}^+\).
Per i restanti archi \(e \in B\) il leader deve fissare un costo \(p(e) \in \mathbb{R}^+\).
Le funzioni \(c(\cdot)\) e \(p(\cdot)\) messe assieme definiscono la seguente funzione di pesatura \(w: E \to \mathbb{R}^+\)
\[\forall e \in E: \,\, w(e) := \begin{cases} c(e) \,\,&,\,\, e \in R \\ p(e) \,\,&,\,\, e \in B \\ \end{cases}\]
Il compito del follower è quello di costruire un MST di \(G\) rispetto alla pesatura \(w\) ottenuta dal leader.
Fissato un MST di \(G_w\) il profitto del leader è dato da
\[\text{leader profit} = \sum_{e \in E(T) \cap B} p(e)\]
L'obiettivo del gioco consiste nel trovare la funzione di pesatura \(p(\cdot)\) che massimizza il profitto.
Osservando le regole del gioco è subito chiaro che in questo gioco è presente un trade-off tra il peso degli archi in B e il guadagno finale. In particolare, se il leader aumenta troppo il peso degli archi in B, allora al follower converrà comprare solo archi in R, facendo guadagnare poco al leader. Detto questo, i pesi degli archi in B devono comunque essere abbastanza alti per permettere al leader di guadagnare qualcosa.
2.1 Example
Andiamo a vedere un esempio dello stackelberg MST game. Nei seguenti esempi gli archi saranno colorati di vari colori utilizzando il seguente schema:
Gli archi rappresentano archi in \(R\), che sono archi il cui peso è scelto in modo statico all'inizio del gioco.
Gli archi rappresentano archi in \(B\), che sono archi il cui peso deve essere scelto dal leader definendo la funzione di pesatura \(p(\cdot)\).
Gli archi infine sono gli archi che il follower sceglie di includere nella costruzione del MST. Di questi archi verdi, il peso di quelli che originariamente erano blu dovrà essere aggiunto al guadagno finale del leader.
Consideriamo quindi la seguente istanza.
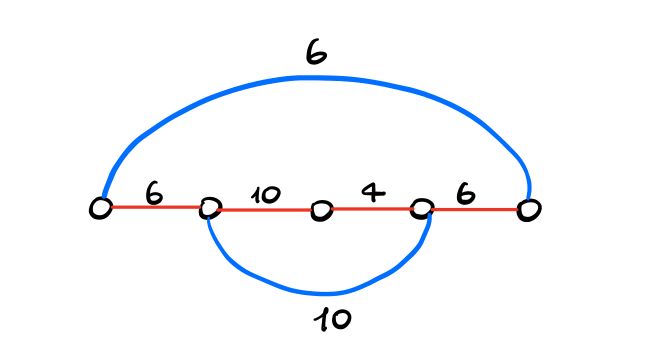
Una volta che il leader ha scelto i pesi degli archi blu, il follower può utilizzare l'algoritmo di kruskal per ottenere il seguente MST
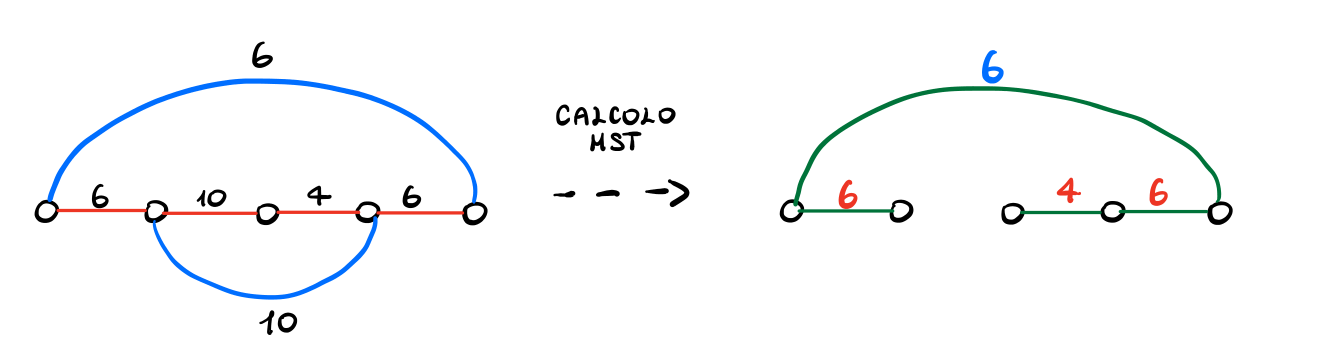
Il guadagno del leader in questo caso è \(6\). È possibile però fare di meglio, come mostra la seguente pesatura.
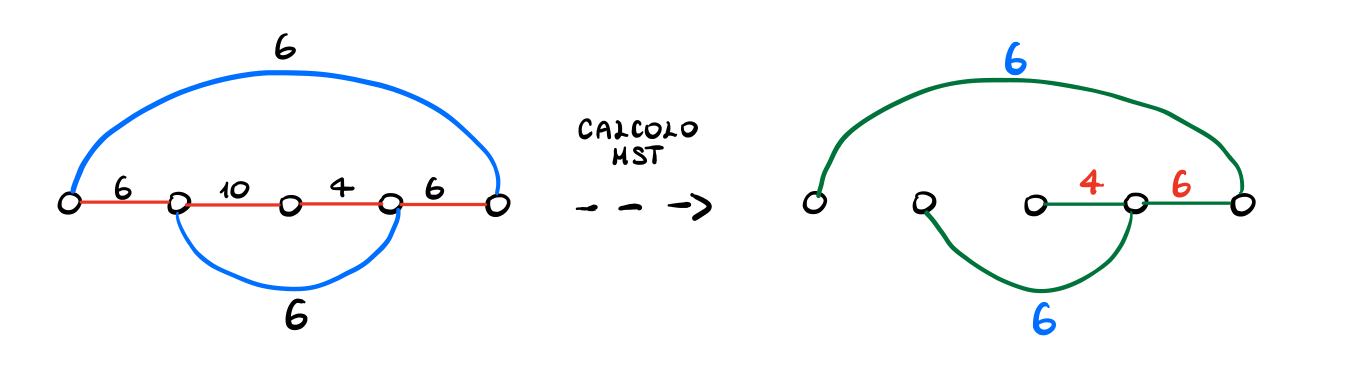
Il guadagano adesso infatti è di 12!
2.2 Assumptions
Prima di analizzare il problema è importante esplicitare le seguenti assunzioni:
Il grafo \(G\) deve contenere uno spanning tree composto da soli archi rossi. Se così non fosse infatti non sarebbe possibile dare un limite superiore al guadagno ottimale del leader.
Tra tutti gli archi con lo stesso peso, quelli blu sono sempre i preferiti. Notiamo che se riusciamo ad ottenere un guadagno \(r\) con questa assunzione, allora anche rimuovendola siamo comunque in grado di ottenere un guadagno di \(r - \epsilon\), con \(\epsilon > 0\) abbastanza leggermente i pesi.
Siamo adesso in grado di analizzare il gioco sotto due aspetti diversi:
Un risultato di NP-hardness;
Un algoritmo approssimante.
3 NP-Hardness Result
Per iniziare osserviamo che fissata una pesatura \(p(\cdot)\), il guadagno del leader non dipende dal particolare MST scelto dal follower. Infatti, siano \(w_1 < w_2 < \ldots < w_h\) i pesi degli archi ordinati. L'algoritmo di Kruskal lavora in \(h\) fasi. Nella fase \(i\) considera:
Prima tutti gli archi blu di peso \(w_i\) (se esistono);
poi tutti gli archi rossi di peso \(w_i\) (se esistono);
Ora, è possibile dimostrare formalmente che il numero di archi blu di peso \(w_i\) che vengono selezionati non dipende dal particolare ordine in cui gli archi blu (prima) e quelli rossi (dopo) vengono considerati. Questo significa che in ogni round i diversi MST che possono essere ottenuti portano tutti lo stesso guadagno al leader. Da questo fatto segue
Lemma 1: In ogni funzione di pesatura \(p(\cdot)\) ottimale, i prezzi assegnati agli archi blu presenti in qualche MST appartengono all'insieme \(\{c(e): \,\, e \in R\}\).
Per capire intuitivamente perché questo risultato vale, supponiamo che gli archi rossi possono essere pesati con \(1\) o con \(5\). Formalmente,
\[\forall e \in R: \,\, c(e) \in \{1, 5\}\]
e poniamo la seguente domanda: ha senso pesare una arco blu \(e' \in B\) tale che
\[1 < p(e') = 3 < 5\]
La risposta è negativa: questo tipo di pesatura non è mai conveniente. Infatti, per Kruskal l'arco e' verrà considerato dopo tutti gli archi rossi di peso \(1\) e prima di tutti gli archi rossi di peso \(5\). Dato però che gli archi blu hanno una priorità su quelli rossi, posso semplicemente porre \(p(e') = 5\) senza spostare l'ordine in cui l'arco \(e'\) viene visto in relazione agli archi rossi, ottenendo in questo modo un guadagno non peggiore. In altre parole, in una qualsiasi pesatura ottima il peso che il leader dà ad ogni arco deve essere uguale al peso di un arco rosso.
Presentiamo adesso un risultato tecnico sulla struttura della soluzione ottima.
Lemma 2: Sia \(p(\cdot)\) una funzione di pesatura ottimale, e sia \(T\) il rispettivo MST. Supponiamo che esiste un arco rosso \(e \in T\) e un arco blu \(f \not \in T\) tale che \(e\) appartiene all'unico ciclo \(C\) in \(T + f\). Graficamente,
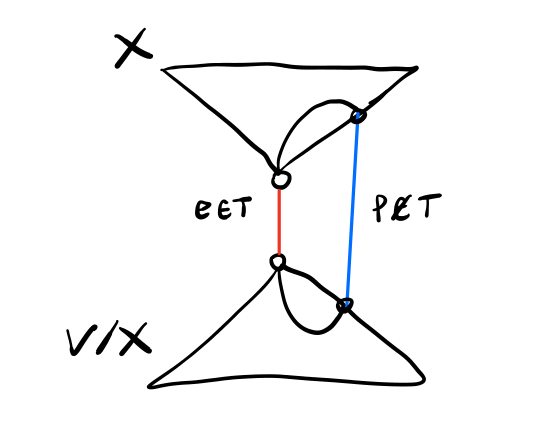
Allora esiste un arco blu \(f'\) diverso da \(f\) in \(C\) tale che
\[c(e) < p(f') \leq p(f)\]
dim: Per come funziona l'algoritmo di Kruskal, dal fatto che \(e\) ed \(f\) appartengono al ciclo \(C\) in \(T + f\) (e quindi in \(G\)), dato che \(e\) è un arco rosso ed è stato scelto, mentre \(f\) è un arco blu e non è stato scelto, abbiamo che \(e\) è stato visto prima di \(f\), e quindi necessariamente \(c(e) < p(f)\).
Sia quindi \(f' \in T\) l'arco blu più pesante in \(C\) che sia diverso da \(f\). Dato che \(f'\) e \(f\) appartengono allo stesso ciclo \(C\), e dato che \(f'\) viene scelto e \(f\) no, abbiamo che \(p(f') \leq p(f)\).
Ora, se fosse \(p(f') \leq c(e)\), potrei cambiare il peso dell'arco \(f\) e farlo diventare \(p(f) = c(e)\). Così facendo l'arco \(e\) rosso esce e l'arco \(f\) blu entra. Dato che i restanti archi blu in \(C\) non vengono toccati in quanto hanno un peso \(\leq f' \leq c(e)\), abbiamo trovato una soluzione migliore, il che non è possibile. Dunque necessariamente \(p(f') > c(e)\).
\[\tag*{$\blacksquare$}\]
Possiamo adesso procedere dimostrando il seguente risultato
Teorema: Lo stackelberg MST game è NP-Hard anche quando \(c(e) \in \{1, 2\}\) per ogni \(e \in R\).
A tale fine si effettuerà una riduzione partendo dal problema del minimum set cover (MSC).
3.1 Minimum Set Cover
Il problem MSC è così definito:
Input:
Insieme di oggetti \(U = \{u_1, u_2, \ldots, u_n\}\).
Insieme di sottoinsiemi di \(U\), \(S = \{S_1, \ldots, S_m\}\), con \(S_j \subseteq U\)
Objective: Trovare un cover \(C \subseteq S\), ovvero un sottoinsieme di \(S\) tale che
\[\bigcup\limits_{x \in C} x = U\]
e minimizzare la sua taglia \(|C|\).
3.2 Reduction
Sia \(I = \langle U, S\rangle\) una istanza del MSC. Prima di iniziare assumiamo l'esistenza di un elemento \(u_n \in U\) che fa parte di ogni sottoinsieme \(S_j\). Formalmente \(\forall S_j \in S: \exists u_n \in U: u_n \in S_j\). Notiamo che questa assunzione non modifica la complessità del problema.
Data l'istanza \(I\) con \(U = \{u_1, \ldots, u_n\}\) e \(S = \{S_1, \ldots, S_m\}\) costruiamo il seguente grafo \(G = (V, R \cup B, w)\).
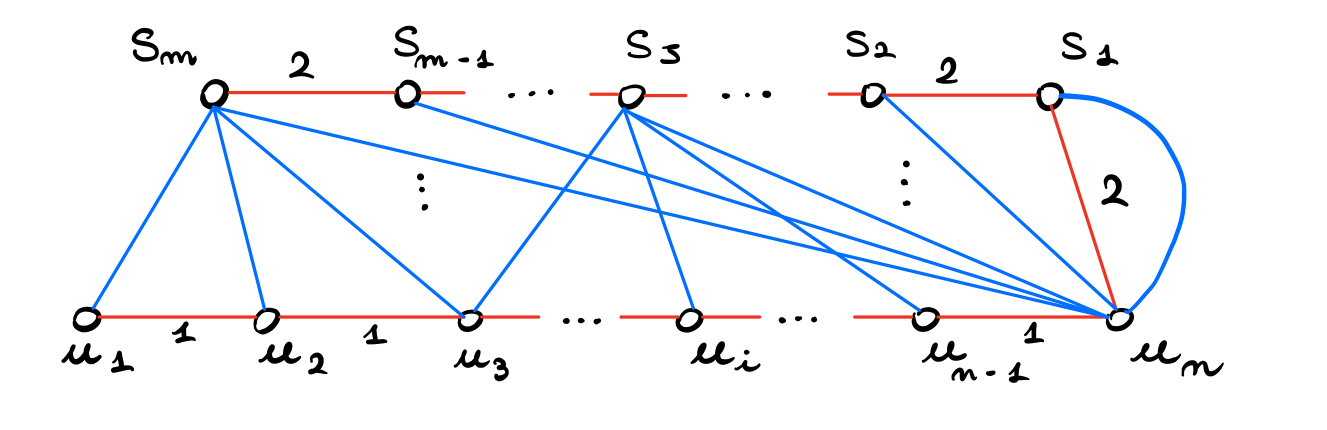
dove gli archi connettono \(u_i\) a \(S_j\) se e solo se \(u_i \in S_j\). Formalmente,
\[ B := \{(u_i, S_j): \,\, u_i \in S_j \text{ in } I\}\]
Per capire meglio la riduzione vediamo qualche pesatura semplice che il leader può effettuare:
Tutti i pesi a 2: In questo caso applicando Kruskal costruiamo come prima cosa il cammino rosso che collega tutti i nodi tra loro
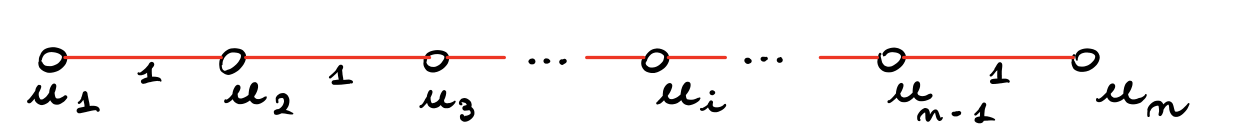
dopo questo prendiamo un arco blu di costo \(2\) per toccare ogni sottoinsieme
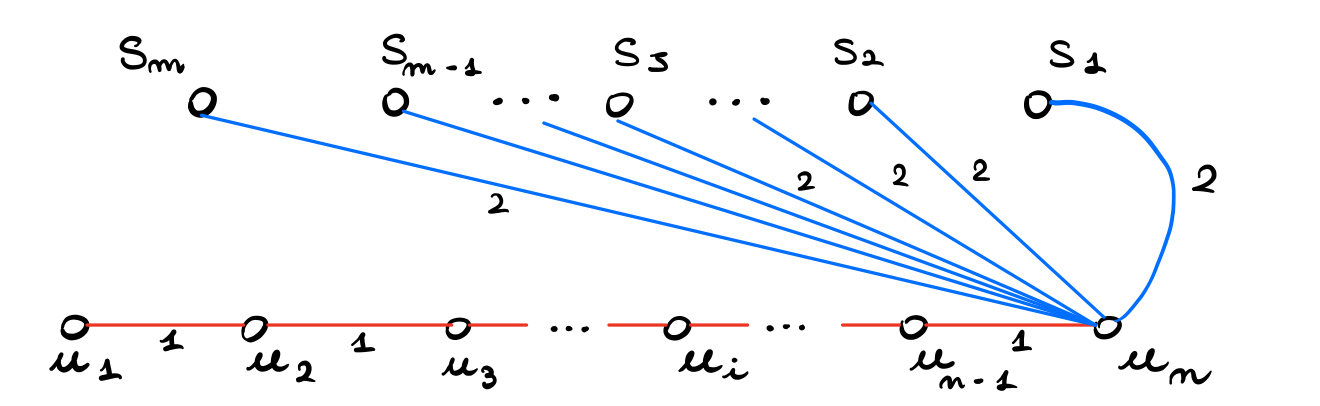
Tutti gli MST ottenibili in questo modo portano dunque un guadagno di \(2m\) al leader.
Tutti i pesi a 1: In questo caso prima vengono scelti tutti gli archi blu che collegano un sottoinsieme \(S_j\) ad un nodo \(n_i\) per ogni nodo \(n_i\) del grafo
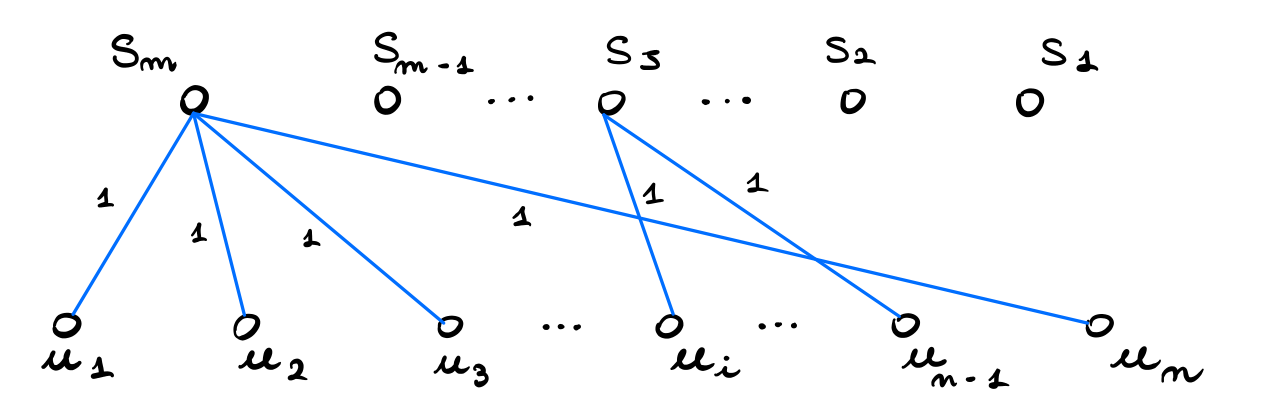
e poi un ulteriore arco blu per ciascuno dei restanti \(t\) sottoinsiemi non ancora toccati.
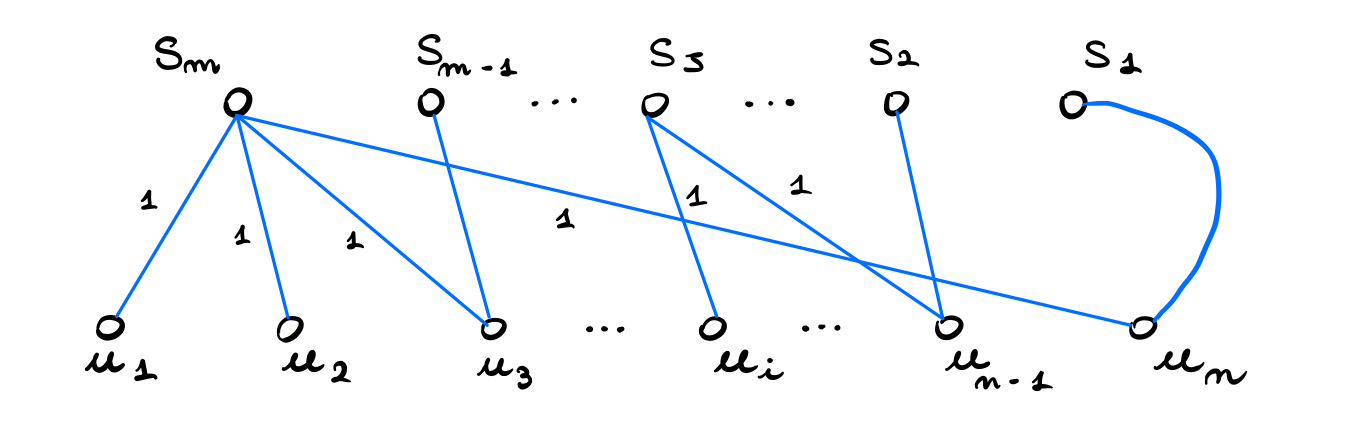
In questo modo ho un MST formato completamente da archi blu, e quindi il guadagno totale è \(n + m - 1\).
Da questi esempi è possibile intuire che al leader possa convenire il seguente approccio: pesare con \(1\) il numero sufficient di archi per poter coprire tutti i nodi \(n_i\), e pesare con \(2\) i restanti archi. In particolare, supponiamo di avere un set cover \(C\) di size \(t\). Definiamo quindi la seguente pesatura
\[\forall e = (u_i, S_j) \in R: \,\, p(e) = \begin{cases} 1 \,\,&,\,\, S_j \in C \\ 2 \,\,&,\,\, \text{ altrimenti } \\ \end{cases}\]
Con questa pesatura il follower prenderà tutti gli archi blu della forma \((u_n, S_j)\) con \(S_j \in C\), che sono \(t\), per i restanti \(n-1\) nodi \(u_i\) prenderà degli archi blu di costo \(1\), e per i tutti i sottoinsiemi che non appartengono al cover \(C\) prenderà degli archi blu di costo \(2\).Il guadagno finale è quindi di
\[t + (n - 1) + 2(m - t)\]
Procediamo quindi dimostrando il seguente claim: \(I = \langle U, S\rangle\) ha un cover set di size \(\leq t\) se e solo se il valore massimo ottenibile dal leader è \(r^{*} \geq n + t - 1 + 2(m - t) = m + 2m - t - 1\).
3.2.1 Part 1: \((\Rightarrow)\)
Sia \(C\) un cover di \(U\) con \(|C| \leq t\).
Utilizzando la pesatura descritta in precedenza, abbiamo che l'MST costruito dal follower fa guadagnare al leader il seguente valore
\[\begin{split} r &= |C| + (n-1) + 2(m - |C|) \\ &= n - 1 + 2m - |C| \\ \geq n + 2m - t - 1 \\ \end{split}\]
\[\tag*{$\checkmark$}\]
3.2.2 Part 2: \((\Leftarrow)\)
Sia \(p: B \to \{1, 2, +\infty\}\) la funzione di pesatura ottimale tale che il rispettivo MST minimizza il numero di archi rossi. Andiamo a dimostrare che:
\(T\) ha solo archi blu
Esiste un cover \(C\) di \(U\) tale che $|C| t.
Per fare questo utilizziamo il seguente
Remark: Se tutti gli archi rossi in \(T\) hanno costo \(1\), allora per ogni arco blu \(e = (u_i, S_j)\) in \(T\) con peso \(2\), abbiamo che \(S_j\) è una foglia in \(T\).
dim: Supponiamo, per assurdo, che la tesi non sia vera. In altre parole supponiamo che in \(T\) abbiamo
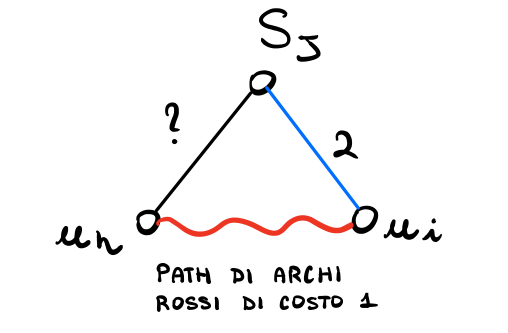
Necessariamente l'arco \((u_h, S_j)\) deve essere un arco blu, in quanto l'unico arco rosso della forma \((u_h, S_j)\) ha costo \(1\), il che è escluso dalle nostre ipotesi.
Notiamo però che abbiamo anche una path di archi rossi di costo \(1\) che collega \(u_h\) a \(u_i\). Questo significa che,
Se l'arco \((u_h, S_j)\) costava \(1\), allora al follower conveniva utilizzare \((u_h, S_j)\) per coprire \(S_j\), e dunque l'arco \((u_i, S_j)\) non sarebbe in \(T\);
Se invece l'arco \((u_h, S_j)\) costava \(2\), allora la sua presenza porta inevitabilmente ad un ciclo, in quanto esiste almeno un cammino di archi rossi di costo \(1\) che collega i nodi \(u_i\) e \(u_h\). Questo significa che dopo aver analizzato tutti gli archi di costo \(1\) i nodi \(u_i\) e \(u_h\) appartengono sicuramente alla stessa componente del MST in costruzione. Ma allora l'aggiunta dei due archi \((u_i, S_j)\) e \((u_h, S_j)\) porterebbe ad un ciclo.
In entrambi i casi quindi, l'esistenza dell'arco \((u_h, S_j)\) ci porta ad una contraddizione.
\[\tag*{$\Huge\unicode{x21af}$}\]
Andiamo adesso a dimostrare che \(T\) ha solamente archi blu.
dim: Sia \(e\) l'arco rosso più pesante in \(T\). Dato che \((V, B)\) è connesso, deve esistere un arco blu \(f \not \in T\). Graficamente,
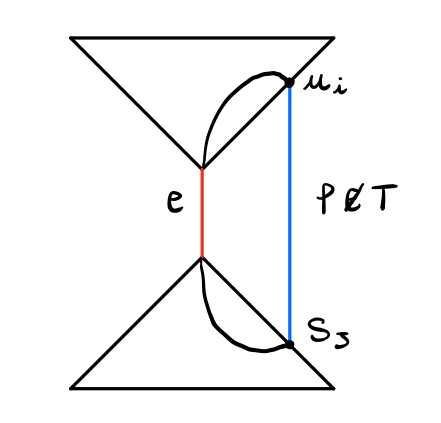
Dal lemma 2 troviamo che esiste un arco blu \(f' \in T:\) tale che \(f' \neq f\) e
\[c(e) < p(f') \leq p(f)\]
Dato poi che in questo grafo i pesi sono presi da \(\{1, 2\}\), abbiamo che per avere \(c(e) < p(f')\) necessariamente \(c(e) = 1\) e \(p(f') = 2\). Ma allora tutti gli archi rossi in \(T\) hanno un peso unitario, e quindi possiamo utilizzare il remark visto prima, che ci dice che \(f'\) è una foglia. Graficamente,
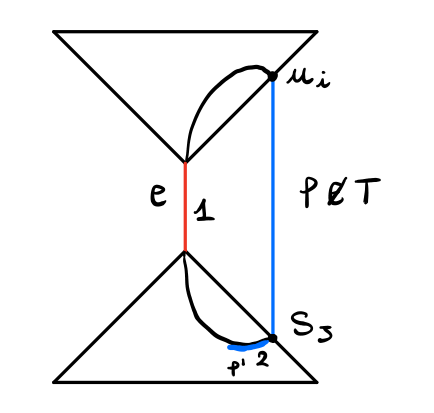
Infatti \(f'\) deve essere della forma \(f' = (u_h, S_j)\) con \(S_j\) foglia. Ma allora tutti gli archi blu restanti in \(C \setminus \{f, f'\}\) hanno peso \(1\).
Questo significa che mettendo \(p(f) = p(f') = 1\) otteniamo un nuovo MST con un guadagno migliore ma con meno archi rossi. Ma \(T\) era l'arco che minimizzava il numero di archi rossi! Troviamo quindi una contraddizione, e concludiamo che \(T\) non può contenere archi rossi.
\[\tag*{$\Huge\unicode{x21af}$}\]
Sia quindi \(T\) un MST di \(G\) formato da soli archi blu. Per finire questo secondo lato della riduzione dimostriamo che esiste un cover di size al più \(t\). A tale fine definiamo
\[C := \{S_j \;\; | \;\; \exists \,\, e = (u_i, S_j) \in B \cap E(T): p(e) = 1 \}\]
In altre parole \(C\) è formato da tutti i sottoinsiemi \(S_j\) tali che nell'MST \(T\) esiste un arco blu di costo \(1\) che incide su \(S_j\). Notiamo che
\(C\) è un cover di \(U\).
Sia infatti \(u_i \in U\). Notiamo che in \(T\) deve esistere un cammino che collega \(u_i\) a \(u_{i+1}\) (o a \(u_{i-1}\)). Dato però che \(T\) non contiene archi rossi, questo cammino deve iniziare con un arco della forma \((u_i, S_j)\). Il costo di questo arco poi deve essere \(1\), in quanto altrimenti al follower sarebbe convenuto prendere l'arco rosso diretto \((u_i, u_{i+1})\). Graficamente,
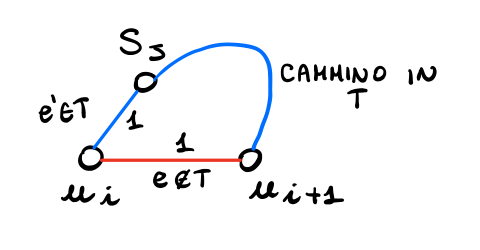
Ma allora \(S_j \in C\) e quindi \(C\) copre ogni elemento di \(U\).
\[\tag*{$\checkmark$}\]
Ogni \(S_j\) non in C è una foglia.
Se \(S_j \not \in C\), allora tutti gli archi blu in \(T\) incidanti a \(S_j\) pesano \(2\). Se \(S_j\) non fosse una foglia si avrebbe
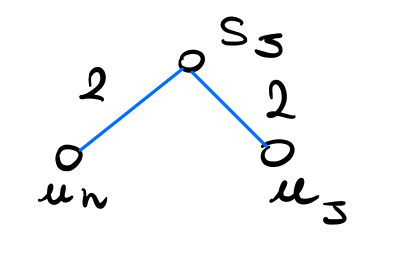
ma questo non converrebbe, in quanto sia \(u_h\) che \(_j\) sono coperti da \(C\) con archi di costo \(1\). Dunque \(S_j\) deve necessariamente essere una foglia.
\[\tag*{$\checkmark$}\]
Mettendo questi due considerazioni assieme otteniamo che il guadagno totale della pesatura ottenuta da \(C\) è pari a
\[2 \cdot (m - |C|) + (n + |C| - 1)\]
Utilizzando l'ipotesi di partenza dunque otteniamo
\[\begin{split} &\;\;\;\;\;\;\;\;\;\;\;\; 2 \cdot (m - |C|) + (n + |C| - 1) \geq n + 2m - t - 1 \\ &\iff n + 2m - |C| - 1 \geq n + 2m - t - 1 \\ &\iff - |C|\geq - t \\ &\iff |C|\leq t \\ \end{split}\]
e quindi \(C\) è un cover di size al più \(t\).
\[\tag*{$\checkmark$}\]
Avendo mostrato entrambi i lati della riduzione abbiamo terminato la dimostrazione della complessità dello stackelberg MST game.
\[\tag*{$\blacksquare$}\]
4 Approximation Result
Anche se calcolare l'ottimo è un problema NP-hard, il seguente algoritmo calcola una approssimazione al nostro problema.
4.1 Single Price Algorithm
Siano \(c_1 < c_2 < \ldots < c_k\) i diversi costi fissati degli archi rossi. Il Single Price Algorithm definisce per ogni costo \(c_i\) la pesatura \(p_{c_i}(\cdot)\) nel seguente modo
\[$\forall e \in B: \,\,\ p_{c_i}(e) := c_i\]
e guarda il guadagno ottenuto con questa pesatura. Alla fine ritorna la pesatura \(p_{c_j}\) che ritorna il migliore guardagno.
Notiamo che il nome dell'algoritmo deriva dal fatto che di volta in volta tutti gli archi blu vengono pesati con lo stesso peso.
4.2 Analysis
Vale il seguente risultato di approssimazione
Teorema: Sia \(\hat{r}\) il guadagno ottimale, e sia \(r\) il guadagno ottenuto applicando il single price algorithm. Allora
\[\hat{r} \leq r \cdot \rho \iff \frac{\hat{r}}{r} \leq \rho\]
dove,
\[\rho := 1 + \min\{\log{|B|}, \log{(n-1)}, \log{\Big(\frac{c_k}{c_1}\Big)}\}\]
dim: Sia \(T\) l'MST associato alla funzione di pesatura ottima, e sia \(h_i\) il numero di archi blu in \(T\) di costo \(c_i\). Esprimendo il guadagno del leader come somma di aree di rettangoli troviamo la seguente figura
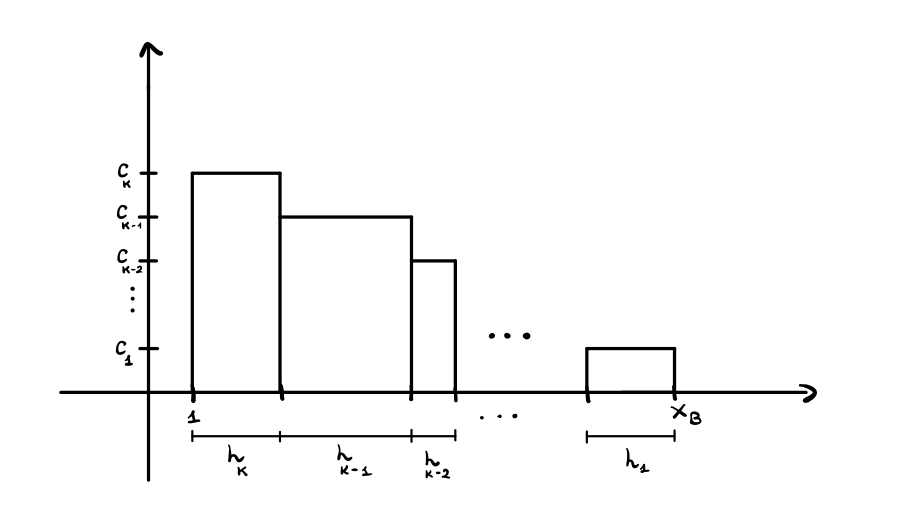
Andiamo adesso a racchiudere questa area totale sotto una curva che segue l'andamento di \(g(x) = 1/x\) e che è tangente ad un vertice di questi rettangoli.
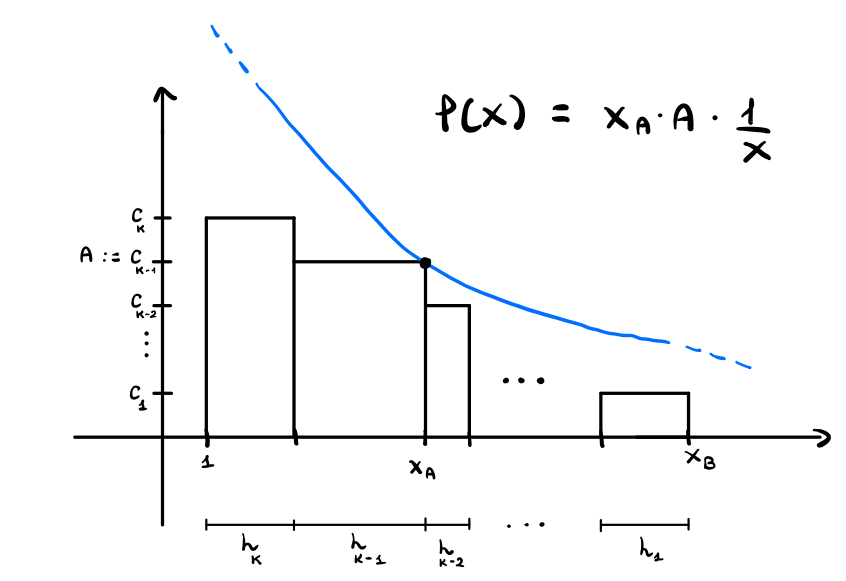
Notiamo che la particolare equazione di questa curva è data da
\[f(x) = x_a \cdot A \cdot \frac1x\]
In questo modo infatti imponiamo che \(f(x_a) = A\). Infine, per avere che la curva si trovi sopra ciascun rettangolo, dobbiamo avere che \(x_a \cdot A \geq c_k\).
Come proprietà della funzione \(g(x) = 1/x\) abbiamo che l'area di ogni rettangolo ha la stessa area. Graficamente,
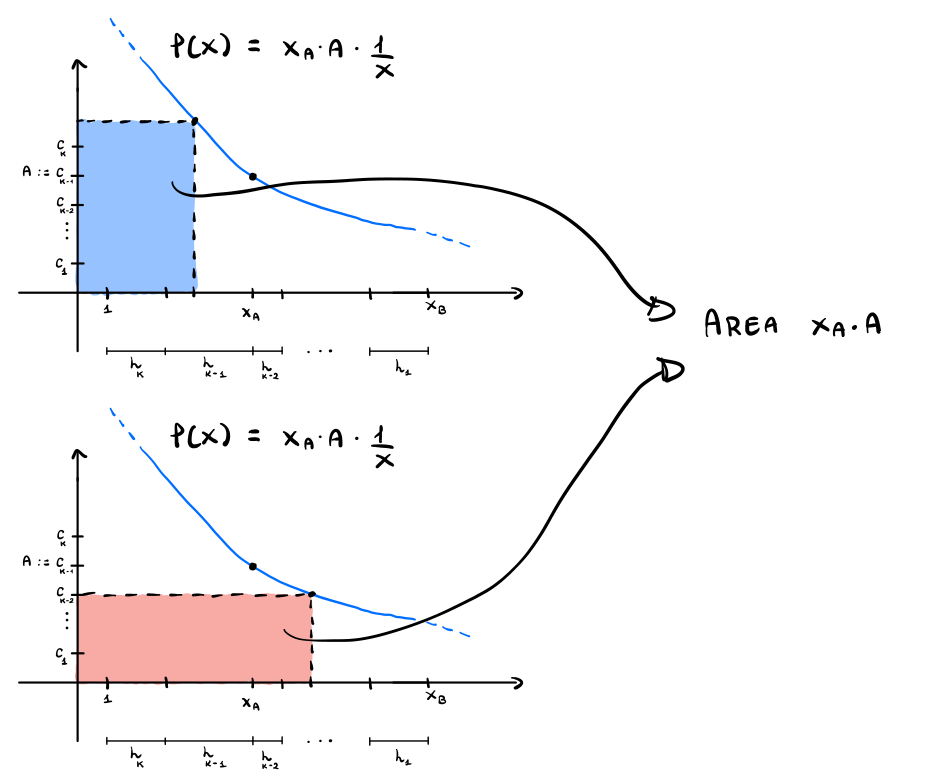
In particolare quindi l'area del rettangolo con base \(1\) è proprio \(x_a \cdot A\).
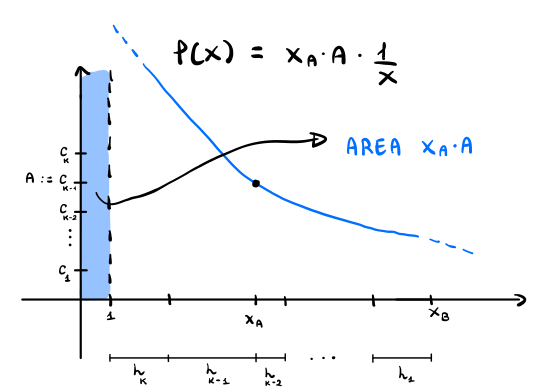
Questo significa che possiamo dare il seguente upper bound al guadagno della soluzione ottima
\[\hat{r} \leq x_a A + \int\limits_{1}^{x_b} x_a \cdot A \cdot \frac1x \,\, dx = x_a A(1 + \log{x_b} - \log{1}) = x_a A (1 + \log{x_b})\]
Andiamo ora a dare dei lower bounds al valore della soluzione calcolata dal nostro single price algorithm. A tale fine iniziamo notando che per come funziona l'algoritmo abbiamo che
\[r = \underset{c_i}{\max} |B| \cdot c_i\]
e quindi, dato che \(A\) è uguale al peso di qualche arco rosso \(c_j\), abbiamo che
\[r \geq |B| c_j \geq x_a c_j = x_a A\]
ovvero
\[\frac{\hat{r}}{r} \leq 1 + \log{x_b}\]
Continuando, notiamo che
\[x_b = \sum_{j} h_j \leq \min\{n-1, |B|\}\]
e quindi
\[\frac{\hat{r}}{r} \leq 1 + \min\{\log{(n-1)}, \log{|B|}\}\]
Per finire, è possibile possibile dimostrare anche che \(\hat{r}/r \leq 1 + \log{\frac{c_k}{c_1}}\). Per fare questo dobbiamo analizzare il grafico di prima pensando però a \(x\) come alla variable dipendente e a \(y\) come alla variable indipendente. Graficamente
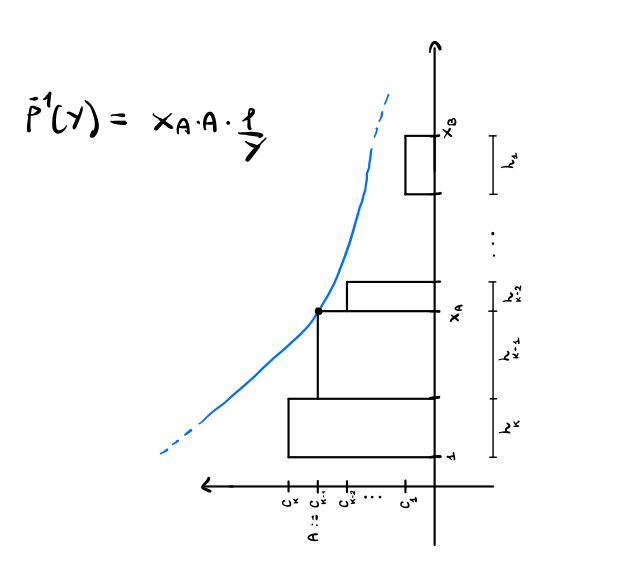
Nuovamente, l'area sotto la curva ci permette di dare un upper bound al guadagno totale. Questa volta però troviamo che
\[\begin{split} \hat{r} \leq x_aA + \int\limits_{c_1}^{c_j} x_aA \frac1y \,\, dy &= x_aA (1 + \log{c_k} - \log{c_1}) \\ &= x_a A \Big( 1 + \log{\frac{c_k}{c_1}}\Big) \\ \end{split}\]
Mettendo tutto assieme troviamo
\[\frac{\hat{r}}{r} \leq 1 + \min\{\log{(n-1)}, \,\, \log{|B|}, \,\, \log{\frac{c_k}{c_1}}\}\]
\[\tag*{$\blacksquare$}\]
4.3 Can We Do Better?
L'analisi appena effettuata ci dice che nel caso peggiore il single price algorithm ci permette di ottenere una approssimazione di \(\theta(\log n)\). In generale però potrebbero esistere altre analisi che migliorano il rapporto di approssimazione. Detto altrimenti, il nostro algoritmo potrebbe essere migliore di quanto dimostrato.
In questo caso però non è così. Infatti esiste un caso in cui l'approssimazione ottenuta dall'algoritmo è proprio \(\theta(\log n)\). Questo ci permette quindi di affermare che l'analisi che abbiamo fatto è "tight", nel senso che con questo particolare algoritmo non possiamo fare meglio di così.
L'esempio menzionato è il seguente

In questo caso la soluzione ottiamle ottiene un guadagno di
$$\hat{r} = ^n \frac{1}{j} = H_n = (n)$
dove \(H_n\) è l'n-esimo numero armonico. Notiamo invece che il single price algorithm invece ottiene al massimo un guadagno di \(r = 1\), in quanto
\[r = \underset{j \in \{1, \ldots, 1/n\}}{\max} j \cdot \frac{1}{j} = \underset{j \in \{1, \ldots, 1/n\}}{\max} 1 = 1\]
5 Exercises
Per finire, consideriamo i seguenti due esercizi:
Dimostrare che in realtà vale anche il seguente fattore di approssimazione
\[\frac{\hat{r}}{r} \leq k\]
dove \(k\) è il numero di pesi diversi per gli archi rossi.
Dato un sottoinsieme aciclico \(F \subseteq B\), trovare una pesatura \(p\) in tempo polinomiale tale che
L'MST associato a \(p\) contiene esattamente \(F\) come insieme di archi blu.
Il guadagno è massimizzato.