AGT - 08 - PLS Completeness

Lecture Info

Data: [2019-01-24 gio]
Sito corso: AGT_2018
Slides: 08 - PLS Completeness
Introduzione: In questa lezione abbiamo introdotto la classe di complessità PLS e abbiamo dimostrato la PLS-completezza del congestion game, una versione generalizzata del global connection game.
Misc: La lezione è basata sui capitoli 19-20 del libro di Roughgarden, "Twenty Lectures on Algorithmic Game Theory".

1 Congestion Game

Iniziamo dal Global Connection Game. In una lezione precedente abbiamo dimostrato che il GCG è un gioco potenziale, e quindi esiste sempre almeno un NE che può essere ottenuto giocando in modo ripetuto tramite la better-response dynamic. In particolare abbiamo visto che la funzione potenziale è definita come segue

\[\Phi(S) := \sum_{e \in E} C_e \cdot H_{K_e(S)}\]

dove $K_e(S)$ rappresenta il numero di giocatori che nel profilo $S$ hanno scelto $e$.

Osserviamo che, anche se la better response converge sempre ad un NE, fino a questo momento nessuno è riuscito a definire una dinamica che, in tempo polinomiale, riesce a raggiungere un NE o una approssimazione di un NE. Non esiste nemmeno un algoritmo polinomiale in grado di calcolare un NE.

Nasce dunque la seguente domanda: è possibile dimostrare che il problema è difficile? Per rispondere alla seguente domanda è stata utilizzata la teoria della PLS-Completezza. Prima di introdurre argomenti di complessità però introduciamo una generalizzazione del CGC: il congestion game.

Il congestion game è così descritto:

Abbiamo un insieme di risorse $E$;
Abbiamo $k$ giocatori;
Ogni giocatore $i$ sceglie una strategia $S_i$ da un particolare sottoinsieme $\mathcal{S}_i \subseteq 2^E$.
Ogni risorsa $e \in E$ ha $k$ possibili costi $c_e(1), c_e(2), \ldots, c_e(k)$, dove intuitivamente $c_e(i)$ rappresenta il costo di $e$ quando viene utilizzato da $i$ giocatori.
Dato un vettore di strategie $S$, il costo per il giocatore $i$ è dato da

\[\text{COST}_i(S) := \sum\limits_{e \in S_i} C_e(k_e(S))\]

dove $k_e(S)$ è il numero di giocatori in $S$ la cui strategia scelta $S_i$ contiene anche $e$.

Osservazione: Il GCG è una particolare istanza del CG in cui le risorse sono gli archi e le strategie i cammini. L'unica differenza è che nel GCG non posso esplicitare tutti i cammini, in quanto sono un numero esponenziale.

Anche il CG è un gioco potenziale. La sua funzione potenziale, chiamata anche Rosenthal potential function, è definita come segue

\[\Phi(S) := \sum_{e \in E} \sum_{i = 1}^{k_e(S)} c_e(i)\]

Da questo segue che anche per i CG esiste sempre un NE, e che giocando in modo iterativo tramite la better-response dynamics siamo in grado di calcolare un NE. Poniamo quindi il seguente problema.

Problema CG-NE: Data una istanza del CG, trovare un qualsiasi NE.

Come vedremo nel corso di questa lezione, per questo problema, molto probabilmente, non esiste un algoritmo polinomiale.

2 Complexity Theory

Per dimostrare la complessità del problema CG-NE un primo possibile approccio potrebbe essere quello di dimostrare che il problema è NP-Hard. Come prima cosa però notiamo che il nostro problema non è un problema di decisione.

Infatti, anche se tradizionalmente si studiano le classi di complessità P e NP, in realtà queste classi rappresentano solamente la punta dell'iceberg. Molti problemi, come il problema CG-NE, non fanno parte di NP, in quanto non sono problemi di decisione. Nasce quindi il bisogno di introdurre delle nuovi classi di complessità che siano significative per classificare i vari problemi affrontati.

A tale fine andiamo quindi a vedere la differenza tra i problemi decisionali e quelli di ricerca, e andiamo ad introdurre una nuova classe di complessità per questi ultimi.

2.1 NP vs FNP

I problema di decisione richiedono di dover rispondere ad una domanda, e dividono le proprie istanze in due sottoinsiemi: l'insieme delle istanze positive, ovvero le istanze che rispondo alla domanda richiesta dal problema in modo positivo, e le istanze negative, che sono le istanze che invece rispondo alla domanda richiesta dal problema in modo negativo.

Esempio: Un tipico problema di decisione è il problema SAT, che prende in input una formula booleana $\phi: X := \{x_1, \ldots, x_n\} \to \{\text{True}, \text{False}\}$ e richiede di rispondere alla seguente domanda: esiste un'assegnazione di verità alle variabili in $X$ che rende vera la formula $\phi$?

Un problema di decisione poi appartiene alla classe NP se, per ogni istanza positiva del problema, è possibile trovare un certificato (in inglese witness) che dimostra il fatto che l'istanza è una istanza positiva. Come vincoli poi il certificato deve essere di lunghezza polinomiale e anche la verifica del certificato deve avvenire in un tempo polinomiale.

Esempio: Il problema SAT appartiene alla classe di complessità NP in quanto è possibile produrre un certificato del genere. Il certificato per SAT in particolare è un'assegnazione di verità: ha una lunghezza polinomiale e ci permette di verificare in tempo polinomiale se la formula può essere soddisfatta o meno.

Non tutti i problemi però sono problemi di decisione. Esistono anche altre tipologie di problemi. Il problema CG-NE ad esempio è un problema di ricerca. Per questi problemi è stata definita un'altra classe di complessità chiamata FNP (Functional NP).

I problemi in FNP sono smili ai problemi in NP. In FNP però per le istanze positive non ci basta dire "si" o "no", ma dobbiamo anche fornire la soluzione trovata. Per risolvere un problema in FNP dobbiamo fornire un algoritmo che prende in input un'istanza del problema e, se l'istanza è positiva, calcola e ritorna una soluzione, altrimenti ritorna "no".

2.2 FNT-Completeness

Seguendo la teoria della complessità classica, è poi possibile introdurre il concetto di FNP-Completezza nello stesso modo in cui si introduce quello della NP-Completezza. È possibile far vedere, ad esempio, che la versione FNP del classico problema SAT è FNP-Completa. Per introdurre questo concetto però bisogna prima introdurre il concetto di riduzione tra due problemi in FNP.

Nel contesti dei problemi di ricerca in FNP, per fare una riduzione tra due problemi $L_1, L_2 \in \text{FNP}$ dobbiamo fornire due algoritmi polinomiali così descritti:

Un algoritmo $A_1$ che trasforma le istanze del problema di partenza $x \in L_1$ in istanze del problema di arrivo $A_1(x) \in L_2$ in modo tale che $A_1(x)$ ha soluzioni sse $x$ ha soluzioni.
Un algoritmo $A_2$ che trasforma le soluzioni (se esistono) dell'istanza del problema di arrivo $A_1(x)$ a soluzioni dell'istanza del problema di aprtenza $x$. Se invece non esistono soluzioni per l'istanza del problema di arrivo $A_1(x)$ allora l'algoritmo deve ritornare "no".

Se abbiamo una riduzione da $L_1$ a $L_2$, ovvero se $L_1 \preceq L_2$, e sappiamo anche risolvere $L_2$ in tempo polinomiale, allora sappiamo risolvere anche $L_1$ in tempo polinomiale utilizzando il seguente schema

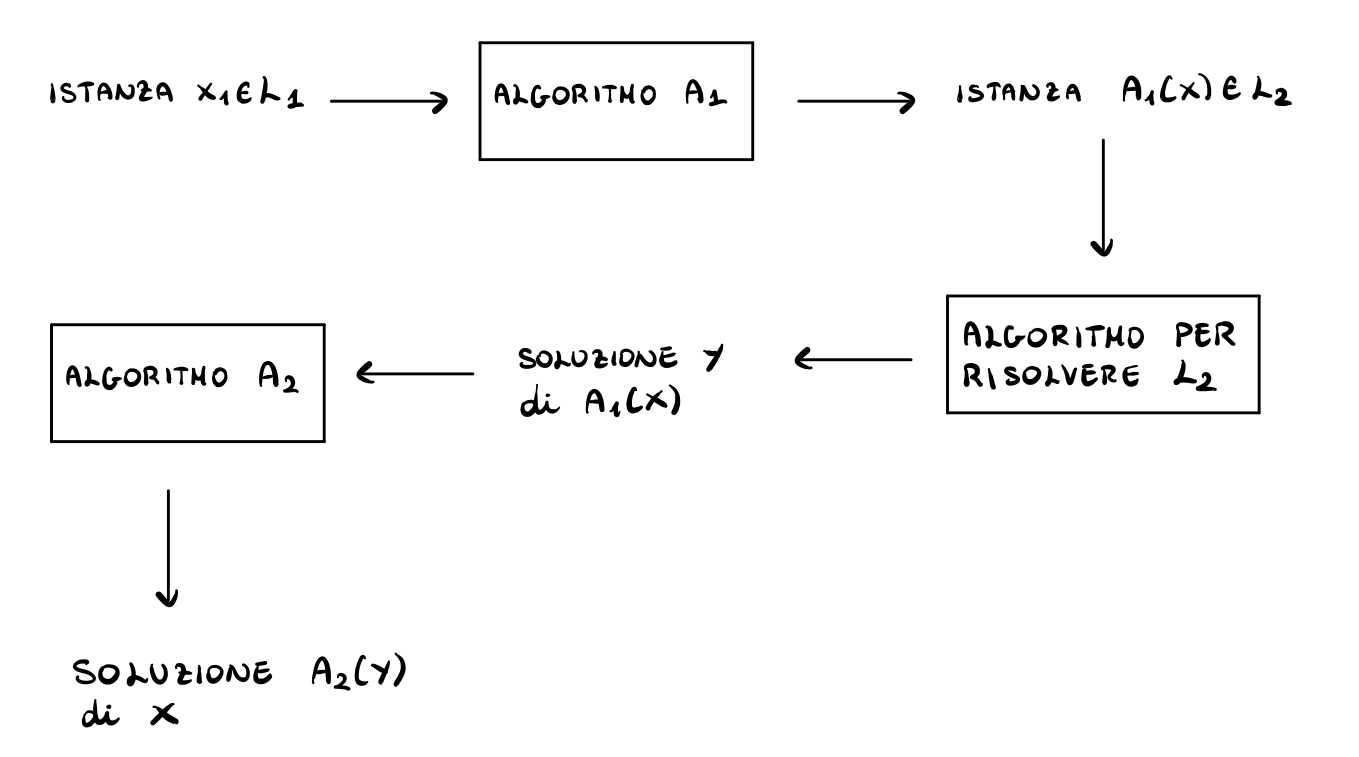
2.2.1 CG-NE is (likely) not FNP-Complete

A questo punto ci potrebbe venire in mente che il nostro problema è FNP-Completo. In realtà vale il seguente

Teorema: Se CG-NE è FNP-Completo, allora NP = coNP

dove ricordiamo che i problemi in coNP sono problemi decisionali che ammettono certificati polinomiali verificabili in tempo polinomiale per le istanze no.

Procediamo con la dimostrazione.

dim: Sappiamo che $\text{CG-NE} \in \text{FNPC}$. Allora esiste una riduzione da $\text{SAT} \in \text{FNPC}$ a $\text{CG-NE}$. Questa riduzione in particolare è composta dai seguenti due algoritmi:

Un algoritmo $A_1(\cdot)$ che trasforma ogni formula booleana $\phi$ di $\text{SAT}$ in una istanza del $\text{CG}$ $A_1(\phi)$.
Un algoritmo $A_2(\cdot)$ che mappa ogni NE $S$ di $A_1(\phi)$ in una assegnazione di verità $A_2(S)$ che soddisfa $\phi$, se esiste almeno un NE, oppure che ritorna la stringa "no".

Sia quindi $\phi$ una formula insoddisfacibile, e sia $S$ un NE di $A_1(\phi)$. Notiamo che il CG è un gioco potenziale, e quindi questo $S$ esiste sempre. Notiamo inoltre che questo $S$ rappresenta anche un (breve) certificato dell'insoddisfacibilità della formula $\phi$. Tale certificato può infatti essere verificato in tempo polinomiale come segue:

A partire da $\phi$ ci si calcola $A_1(\phi)$.
Calcolando la best-response per ogni giocatore si verifica che $S$ è un NE di $A_1(\phi)$.
Si calcola $A_2(S)$ e si verifica che ritorna "no".

Così facendo abbiamo dimostrato che $\text{SAT} \in \text{coNP}$, e quindi che NP $=$ coNP.

\[\tag*{$\blacksquare$}\]

Osservazione: Anche se non si è mai dimostrato che NP $\neq$ coNP, molti esperti pensano questo. Infatti, se NP $=$ coNP dovrebbe essere possibile certificare in tempo polinomiale che una formula di SAT non possa essere soddisfatta.

Dall'ultima osservazione dunque non sembra che CG-NE sia FNP-Completo.

2.3 TFNP

Nella dimostrazione precedente l'unica cosa specifica del problema CG-NE che abbiamo utilizzato è il fatto che in CG esiste sempre un NE. È quindi possibile introdurre un nuova classe di complessità, la classe TFNP, che sta per Total FNP.

Def. La classe TFNP è formata dai problemi in FNP per cui ogni istanza ha almeno una soluzione.

Notiamo che CG-NE $\in$ TFNP. Inoltre, il risultato visto prima può essere esteso a tutti i problemi in questa classe:

Teorema: Se un problema TFNP è FNP-Completo, allora NP = coNP.

Le classi FNP e TFNP sono strutturate nel seguente modo

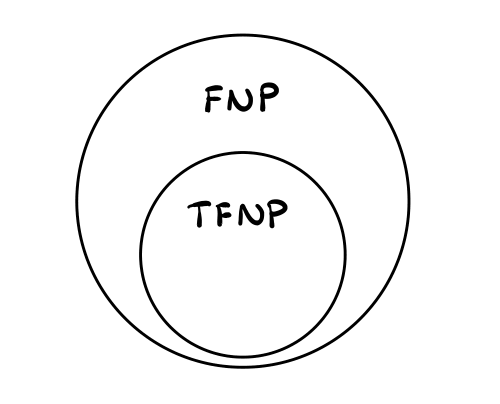
Alcuni problemi interessanti in TFNP sono:

Il problema che stiamo affrontando in questa lezione, ovvero il problema CG-NE.
Il problema di trovare un NE composto da strategie miste per un gioco finito.
Il problema di fattorizzare un intero nei suoi fattori primi.

A questo punto nasce un dubbio naturale: non è forse che CG-NE sia TFNP-Completo? Anche in questo caso la risposta è negativa, e deriva dalla considerazione a seguire.

2.3.1 Syntactic vs Semantic Classes

Fino a questo momento nessuno è mai riuscito a dimostrare l'esistenza di un problema TFNP-Completo. Alcuni ricercatori pensano che questo deriva dal fatto che TFNP è una classe "semantica", e non "sintattica".

Intuitivamente,

Le classi sintattiche sono caratterizzare dal fatto che esiste un modello di calcolo che permette di stabilire se un dato problema appartiene o meno alla classe;
L'appartenenza di un problema ad una classe semantica invece non sembra un qualcosa di riconducibile ad un modello di calcolo generale, ma dipende molto dal contesto in cui il problema è definito. Ad esempio, il fatto che fattorizzare un intero nei suoi fattori primi faccia parte di TFNP dipende molto da come è strutturata e sviluppata la teoria dei numeri; il fatto che esiste sempre un NE ottenibile con strategie miste (l'enunciato del Teorema di Nash) dipende invece da come è strutturata la teoria dei giochi.

2.4 PLS

La classe "giusta" per il problema CG-NE è la classe PLS (Abstract Polynomial Local Search).

Intuitivamente i problemi in PLS sono problemi di ricerca le cui soluzioni sono codificabili come ottimi locali di un qualche problema di ottimizzazione che può essere risolto con un algoritmo di ricerca locale.

Formalmente un problema è in PLS se è possibile individuare i seguenti tre algoritmi:

Un algoritmo polinomiale che prende in input una istanza del problema e ritorna una qualsiasi soluzione ammissibile;
Un algoritmo polinomiale che prende come input una istanza del problema e una soluzione ammissibile e ritorna il valore della funzione obiettivo da ottimizzare sulla soluzione data in input.
Un algoritmo polinomiale che prende come input una istanza del problema e una soluzione ammissibile e ritorna e, o migliora la soluzione data in input rispetto alla funzione obiettivo, oppure ritorna "locally optimal".

Osservazione: Notiamo che per come abbiamo definito la classe PLS, non andiamo a specificare in modo esplicito il significato di "locale". Questo concetto è implicitamente definito nel terzo algoritmo.

Andiamo adesso ad introdurre un problema noto appartenente alla classe PLS: il maximum cut problem.

2.4.1 Maximum Cut Problem

Il problema è così definito:

Input: Abbiamo un grafo non diretto $G = (V, E, w)$ con pesi non-negativi.
Solution: Una soluzione è data da un cut $(X, Y)$ dove $X$ e $Y$ formano una partizione di $V$.
Measure: L'obiettivo è quello di massimizzare il peso totale del taglio $(X, Y)$, che è rappresentato dalla seguente quantità

\[\sum\limits_{\substack{(x, y) \in E: \\ x \in X, \,\, y \in Y }} w(x, y)\]

Questo problema è noto essere NP-Hard. È però possibile utilizzare la seguente euristica, nota come local search algorithm:

Prendo un cut arbitrario $(X, Y)$
Finché riesco a migliorare la soluzione trovata con una mossa locale, lo faccio. In questo caso particolare la mossa locale consiste nel muovere un singolo vertice da un lato del cut ad un'altro lato del cut.

Notiamo che questa euristica non sempre ci porta al massimo globale, come mostra il seguente esempio

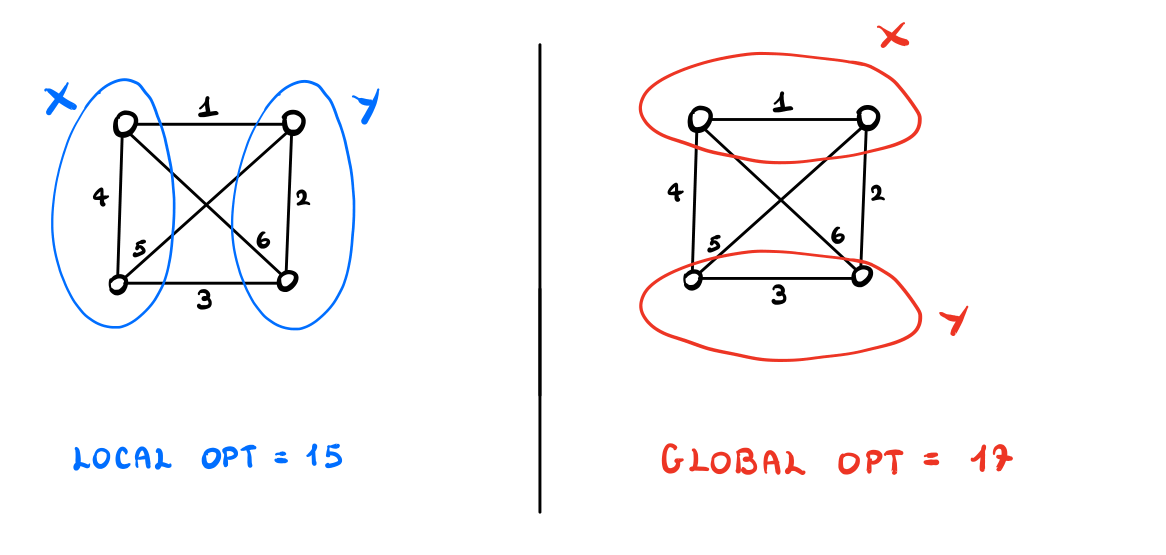
A questo punto ci chiediamo: trovare un ottimo locale è più semplice di trovare un ottimo globale? La risposta a questa è: dipende. Certe volte lo è.

Consideriamo ad esempio le istanze del max-cut su grafi non pesati. In questo caso abbiamo che:

L'ottimo globale rimane difficile da trovare, in quanto il problema resta NP-Hard.
Un ottimo locale invece può essere calcolato utilizzando il local search algorithm.

Se invece il grafo è pesato con pesi generali, allora non è stato ancora trovato un algoritmo di ricerca locale che in tempo polinomiale trova un ottimo locale. In realtà, anche ampliando lo spazio di ricerca e andando oltre gli algoritmi di ricerca locale, ancora non si è trovato nulla.

Per il problema max-cut in particolare valgono i seguenti due risultati:

Teorema 1 (Risultato negativo condizionale): Calcolare un massimo locale di un'istanza di max-cut con valore dei pesi degli archi non negativo è un problema PLS-Completo

Teorema 2 (Risultato negativo non-condizionale): Calcolare un massimo locale di un'istanza di max-cut con valore dei pesi degli archi non negativo utilizzando un algoritmo di ricerca locale può richiede un numero di iterazioni esponenziale in $|V|$, indipendentemente da quale scelta facciamo ad ogni iterazione.

Osservazione: Il teorema 1 è un risultato analogo al Teorema di *Cook, che dimostra la NP-Completezza di SAT.

2.4.2 Reductions in PLS

Dati due problemi $L_1, L_2 \in$ PLS, per costruire una riduzione da $L_1$ a $L_2$ ($L_1 \preceq L_2$) dobbiamo definire i seguenti due algoritmi:

Un algoritmo $A_1(\cdot)$ che trasforma istanze del problema di partenza $x \in L_1$ in istanze del problema di arrivo $A_1(x) \in L_2$.
Un algoritmo $A_2(\cdot)$ che trasforma un ottimo locale dell'istanza di arrivo $A_1(x) \in L_2$ in un ottimo locale dell'istanza di partenza $x \in L_1$.

Un problema $L$ è poi detto PLS-Completo se $L \in$ PLS e se tutti i problemi in PLS possono essere ridotti ad $L$.

2.5 PPAD

nil

3 CG-NE is PLS-Complete

Avevamo menzionato il fatto che la classe PLS era quella "giusta" per il problema CG-NE. Questo deriva dal seguente risultato.

Teorema: Il problema CG-NE è PLS-Completo.

La dimostrazione di questo teorema verrà divisa in due step: prima facciamo vedere che CG-NE fa parte di PLS, e poi riportiamo una riduzione da Max-Cut a CG-NE.

dim:

3.0.1 CG-NE $\in$ PLS

Facciamo vedere inizialmente che CG-NE fa parte della classe PLS Per fare questo necessitiamo delle seguenti tre osservazioni:

Data una istanza, è banale costruire in tempo polinomiale un qualsiasi profilo di strategie $S$.
Data una istanza, la funzione obiettivo che consideriamo è la funzione potenziale $\Phi(S)$, che per come è definta può essere calcolata in tempo polinomiale.
Infine, data una istanza e un profilo $S$, è possiible in tempo polinomiale calcolare la best response per ogni player e ottenere un nuovo, migliore, profilo $S'$, oppure ritornare "S è un NE".

\[\tag*{$\checkmark$}\]

3.0.2 Max-Cut $\preceq$ CG-NE

Mostriamo adesso una riduzione da Max-Cut a CG-NE. A tale fine, sia $I = \langle G(V, E, w) \rangle$ una istanza di Max-Cut e costruiamo la relativa istanza di CG-NE nel seguente modo:

Abbiamo un giocatore per ogni vertice $v \in V$.
Abbiamo due risorse $r_e$ e $\bar{r}_e$ per ogni arco $e \in E$.
Le strategie per il giocatore $v$ sono due, e sono le seguenti

\[S_v := \{r_e \,\, : \,\, e \in \delta(v)\} \;\;\;,\;\;\; \bar{S}_v := \{\bar{r}_e \,\, : \,\, e \in \delta(v)\}\]

dove $\delta(v)$ contiene tutti gli archi in $G$ incidenti a $v$.
I possibili costi per la risorsa $r \in \{r_e, \bar{r}_e\}$ sono i seguenti

\[c_r(0) := 0 \;\;,\;\; c_r(1) := 0 \;\;,\;\; c_r(2) := w(e)\]

Con questa costruzione è possibile costruire una biiezione tra i $2^{|V|}$ possibili profili di strategia del gioco di arrivo e i tagli del grafo di partenza. In particolare, fissato un profilo $S$, il corrispettivo taglio del grafo è dato da $(X_S, Y_S := V \setminus X_S)$ con

\[X_s := \{V: \,\, \text{in } S \text{, } v \text{ gioca } S_v\}\]

Notiamo infine che con questo mapping abbiamo che

\[\begin{split} & \;\;\;\;\;\;\;\;\;\;\; (X_S, Y_S) \text{ è un cut localmente massimale di } G \\ &\iff S \text{ è un minimo locale di } \Phi(S) \\ \end{split}\]

Infatti, se consideriamo il valore della funzione potenziale fissato un profilo $S$

\[\Phi(S) = \sum\limits_{e \in R} \sum\limits_{i = 1}^{k_r(S)} C_r(i)\]

notiamo che ogni arco $e = (u, v)$ in cui $u$ e $v$ fanno parte di componenti diverse ha contributo $0$, mentrse ogni arco $e = (u ,v)$ in cui $u$ e $v$ fanno parte della stessa componente ha contributo $w(e)$. Ma quindi,

\[\Phi(S) = \sum\limits_{e \in R} \sum\limits_{i = 1}^{k_r(S)} C_r(i) = W - W(X_S, Y_S)\]

dove $W := \sum_{e \in E} w(e)$ è la somma totale dei pesi di ogni arco. Avendo esplicitato la relazione tra il valore di $\Phi(S)$ e il valore del rispettivo taglio, risulta banale notare che per minimizzare $\Phi(S)$ dobbiamo necessariamente massimizzare $W(X_S, Y_S)$.