AR - 01 - Introduzione
Lecture Info
Data:
Introduzione: In questa lezione abbiamo introdotto i principali temi studiati in analisi di reti.
1 Analisi di Reti
Una rete è un insieme di relazioni.
Per analisi di reti si intende l'utilizzo di strumenti e metodologie--riprese da vari campi della conoscenza umana, tra cui troviamo sicuramente la matematica e l'informatica, ma anche l'economia e la sociologia--al fine di studiare una rete sotto diversi punti di vista.
Esistono svariate tipologie di reti, tra cui troviamo:
Reti fisiche;
Reti sociali;
Reti di informazioni (come il Web);
A seconda della tipologia di rete che abbiamo di fronte ci possiamo porre diverse domande. Ad esempio, nelle reti sociali, che sono reti in cui i nodi rappresentano individui e i cui archi rappresentano relazioni umane tra individui, possiamo studiare la stabilità della rete, ovvero la tendenza della rete a non cambiare struttura. Sempre nelle reti sociali è anche possibile studiare come le relazioni modificano il comportamento degli individui. Infine, sempre nelle reti sociali, è anche possibile studiare come, certe volte, è la sola esistenza della rete a cambiare il comportamento degli individui.
1.1 Esempio 1: Stabilità
Supponiamo di avere una rete sociale in cui ci sono tre individui: \(A\), \(B\) e \(C\).
L'individuo \(A\) è un amico stretto sia di \(B\) che di \(C\). Invece, gli individui \(B\) e \(C\) non vanno molto d'accordo. Si può intuire che la rete sociale appena descritta formata dal gruppo di tre individui non è una rete "stabile". Infatti, sarà difficile per \(A\) mantenere uno stretto rapporto di amicizia con entrambi \(B\) e \(C\), in quanto, ad esempio, se \(A\) esce con \(B\) allora non può uscire con \(C\) e viceversa. Se invece non c'è questo conflitto tra \(B\) e \(C\), oppure se \(A\) è solo amico di \(B\) oppure di \(C\), allora la rete diventa "stabile".
Questo esempio ci fa vedere come le relazioni all'interno di una rete sono capaci di modificare le strutture all'interno di una rete.
1.2 Esempio 2: Influenza
La professoressa Di Ianni vive più o meno nella zona di Ostia. Per arrivare all'università ha due scelte: prendere la via del mare oppure prendere l'ostiense. Generalmente prende la via del mare, in quanto la via ostiense è una strada locale.
Se un giorno però la Di Ianni dovesse vedere una serie di macchine che cambiano repentinamente direzione e si immettono nella via ostiense, molto probabilmente penserebbe che queste macchine sanno qualcosa che lei non sa, e dunque questa informazione sul comportamento degli altri individui potrebbe far cambiare il comportamento della DI Ianni, facendole scegliere l'ostiense al posto della via del mare.
Questo è un piccolo esempio che descrive come un individuo che appartiene ad una determinata rete sociale può cambiare il proprio comportamento se riceve informazioni da altri individui appartenenti alla stessa rete sociali.
1.3 Rappresentare una Rete
Al fine di rappresentare una rete utilizziamo il modello matematico del grafo. Un grafo \(G = (V, E)\) è definito come una coppia di insiemi, in cui \(V = \{v_1, v_2, ..., v_N\}\) è l'insieme dei vertici del grafo, mentre \(E \subseteq V \times V\) è l'insieme degli archi del grafo. Utilizzando il grafo come modello matematico di una rete possiamo studiare sicuramente almeno le seguenti cose:
Lo studio delle comunità del grafo, ovvero lo studio delle parti più "densamente connesse".
Lo studio della connettività della rete, ovvero l'eventuale presenza di componenti connesse e di componenti fortemente connesse, in caso di grafi diretti.
Lo studio del diametro della rete, dove con diametro intendiamo la massima distanza tra due nodi nel grafo. Ovvero, volendo essere formali, e ricordando la definizione per \(d_G(u, v)\) come la lunghezza di un cammino minimo che da \(u\) a \(v\), troviamo la seguente definizione
\[ Diam(G = (V, E)) := \max_{u, v \in V }d_G(u, v) \]
2 Esperimenti Sociali
Andiamo adesso a discutere di alcuni importanti esperimenti che sono stati fatti nel contesto delle reti sociali.
2.1 Componente Gigante (Leskovec e Hrovitz)
In questo articolo, chiamato "Planetary-Scale Views on an Instant-Messaging Network", e presente al seguente link, Leskovec e Hrovitz hanno avuto accesso ai dati generati in un mese un sistema telefonico di comunicazione, sviluppato da Microsoft e chiamato ``Instant Messaging''.
I dati sono stati utilizzati per costruire una rete sociale, in cui i nodi erano gli utenti e le connessioni erano i tentativi di comunicazioni tra un utente e l'altro.
Si è scoperto, tra le altre cose, che all'interno del grafo c'era una componente fortemente connessa che conteneva un sacco di invidui. Su 240 milioni di utenti totali infatti, la componente scoperta ne conteneva 200 milioni.
2.2 Gradi di Separazione (Milgram)
In questo esperimento, noto come small-world experiment, e disponibile al seguente link, Milgram e altri ricercatori hanno studiato la media della lunghezza dei cammini presenti nella rete sociale formata dalla popolazione degli stati uniti.
In particolare si è trovato che, in media, tale lunghezza è \(6\). Questo vuol dire che generalmente ci sono intorno alle \(6\) persone che permettono di passare da una data persona \(x\) ad un'altra persona \(y\), qualunque siano queste persone \(x, y\) all'interno della rete sociale in questione.
Da questo esperimento è poi diventato famoso il concetto dei "6 gradi di separazione".
3 Grafi Aleatori
Idealmente vorremmo studiare le reti "reali", ovvero le reti che vengono attualmente utilizzare, in qualche forma o modo, dalle persone o dai computer. Dato che però il più delle volte è difficile mettere le mani su reti molto grandi, in quanto chi le possiede generalmente non è interessato a darcele così facilmente, nel campo della ricerca si è molto spesso costretti a creare dei modelli di rete aleatorie, che ci permettono di generare grafi molto grandi.
Una volta definito un modello ci dobbiamo però chiedere: Quanto è utile questo modello? In altre parole: quanto è aderente alla realtà che sta cercando di modellare? Al fine di rispondere a queste domande dobbiamo studiare varie proprietà del modello, per vedere se i risultati ottenuti corrispondono a quello che ci aspettiamo di vedere nel mondo reale, o quello che abbiamo visto tramite degli esperimenti effettuati su delle reti reali.
Al fine di costruire un modello generativo di grafi dobbiamo scegliere:
Il numero di nodi
Una regola che ci permetta di stabilire se tra due nodi c'è un arco oppure no.
3.1 Modello di Erdős-Rényi
Un grafo casuale generato con il modello di Erdős-Rényi \(G_{n,p} = (V, E)\), è un grafo tale che:
\(V = [n] := \{1, 2, ..., n\}\).
\(\forall u, v \in [n], \,\, P((u, v) \in E) = \begin{cases} 0 &, u = v \\ p &, \text{ altrimenti } \\ \end{cases}\)
Ovvero \(G\) ha \(n\) nodi, con \(n \in \mathbb{N}\), e la probabilità che ci sia un arco tra una coppia di nodi distinti \(u, v \in V\) è \(p\), con \(0 \leq p \leq 1\).
3.1.1 Grado Medio
Ricordando che il grado medio del grafo è dato dalla seguente equazione
\[\text{ grado medio } = \frac{ \sum_{i = 1}^n \text{ grado nodo } i}{ \text{# nodi}}\]
ci possiamo quindi chiedere: qual'è il grado medio per un grafo \(G_{n,p} = (E, V)\) generato con il modello di Erdős-Rényi?
Per rispondere a questa domanda occorre notare che, dato che \(G_{n,p} = (E, V)\) è un grafo aleatorio, non ha senso calcolare il grado medio, in quanto il grado di ogni nodo \(i\) non è un valore deterministico ma è dato da una precisa distribuzione di probabilità. Al posto di calcolare il grado medio possiamo però calcolare il valore atteso del grado del nodo \(i\).
Al fine di calcolare tale valore definiamo con \(d_i\) il grado del nodo \(i\). Sia poi \(x \in V \setminus \{i\}\), definiamo quindi la v.a. \(Y_x\) indichiamo la v.a. definita da
\begin{equation*} Y_x = \begin{cases} 1 & (i, x) \in E \\ 0 & (i, x) \not \in E \\ \end{cases} \end{equation*}Dalla definizione di \(Y_x\) segue che \(d_i = \sum_{x \in V: x \neq i} Y_x\). Ma allora, dalla linearità della media, e dal fatto che le \(Y_x\) sono i.i.d. con valore atteso pari a
\begin{equation*} \mathbb{E}[Y_x] = 1 \cdot P((i, x) \in E) + 0 \cdot P((i, x) \not \in E) = 1 \cdot p = p \end{equation*}abbiamo che
\begin{equation*} \mathbb{E}[d_i] = \sum_{x \in V: x \neq i} \mathbb{E}[Y_x] = \sum_{x \in V: x \neq i} p = (n-1) \cdot p \end{equation*}dunque il grado medio del nodo \(i\) è pari a \((n-1) \cdot p\).
4 Rich get Richer
All'interno delle reti sociali è presente un fenomeno, chiamato rich get richer, che fa sì che tanto più un nodo è popolare, e tanto più la sua popolarità aumenta.
Al fine di studiare formalmente questo fenomeno dobbiamo capire come varia il grado di un nodo. Detto altrimenti, dobbiamo studiare la seguente funzione di probabilità al variare di \(k\)
\[ \delta(k) := P(d_i = k) \]
Nel modello di Erdős-Rényi abbiamo che \(d_i\) si comporta come una v.a. binomiale di parametri \((n-1, p)\). Dunque troviamo la seguente funzione
\[ \delta(k) = \binom{n-1}{k}p^k (1 - p)^{n-1-k} \]
4.1 Scelta parametro \(p\)
Supponiamo di voler utilizzare il modello generativo di Erdős-Rényi. Notiamo che nella definizione del nostro modello la scelta del parametro \(p\) è influenzata dal tipo di rete che vogliamo modellare. Ad esempio, se vogliamo modellare una rete sociale, una proprietà che potremmo potenzialmente volere è la seguente
\[\text{il valore atteso del grado di ogni individuo deve essere costante}\]
Andiamo quindi a trovare il giusto parametro per \(p\) al fine di ottenere questa proprietà.
A tale fine imponiamo \(p = \lambda/n\), e riscrivendo la formula, otteniamo
\[\begin{split} \delta(k) &= P(d_i = k) \\ &= \binom{n-1}{k}p^k(1-p)^{n-1-k} \\ &= \binom{n-1}{k}(\frac{\lambda}{n})^k (1 - \frac{\lambda}{n})^{n-1-k} \\ \end{split}\]
Notiamo a questo punto che, per \(n \to \infty\) si ha che \(\frac{\lambda}{n} \to 0\). Ma allora, utilizzando il fatto che \(1 - x \approx e^{-x}\), per \(x \to 0\), otteniamo che, per \(n \to \infty\), è possibile approssimare \(1 - \lambda/n\) con \(e^{-\frac{\lambda}{n}}\), ottenendo quindi la seguente formula
\[\binom{n-1}{k}(\frac{\lambda}{n})^k (1 - \frac{\lambda}{n})^{n-1-k} \approx \frac{(n-1)(n-2)...(n-k)}{k!} (\frac{\lambda}{n})^k e^{-\frac{\lambda}{n}(n-1-k)}\]
Dato poi che per \(n \to \infty\) abbiamo che \(e^{-\frac{\lambda}{n}(n - 1- k)} \approx e^{-\lambda}\), troviamo
\[\begin{split} \delta(k) &\approx \frac{(n-1)(n-2)...(n-k)}{k!} (\frac{\lambda}{n})^k e^{-\lambda} \\ &= \frac{(n-1)(n-2)...(n-k)\lambda^k}{k!n^k} e^{-\lambda} \\ \end{split}\]
Infine, utilizazndo l'approssimazione di Stirling \(k! \approx \sqrt{2 \pi k} (\frac{k}{e})^k\) e prendendo il limite per \(n \to \infty\), otteniamo il seguente risultato
\[\begin{split} \delta(k) &\approx^{n \to \infty} \frac{(n-1)(n-2)...(n-k)}{n^k} \cdot \frac{\lambda^k}{k!} e^{-\lambda} \\ &\approx \frac{\lambda^k}{k!} e^{-\lambda} \\ &\approx \frac{1}{\sqrt{2 \pi k}} (\frac{e}{k})^k \lambda^k e^{-\lambda} \\ &= \frac{e^{-\lambda}}{\sqrt{2 \pi k}} (\frac{\lambda e}{k})^k \end{split}\]
Riassumendo abbiamo dimostrato che, per \(n \to \infty\),
\[\delta(k) = P(d_i = k) \approx \frac{e^{-\lambda}}{\sqrt{2 \pi k}} (\frac{\lambda e}{k})^k\]
e quindi possiamo concludere osservando che
\[\delta(k) \to 0, \text{ per } k \to \infty\]
il che è un risultato ragionevole in una rete sociale. Notiamo inoltre, per finire, che tale funzione tende a \(0\) come \(\frac{1}{k^k}\), ovvero come l'inversa di un esponenziale. Questo risultato sarà importante nello studio del fenomeno rich get richer.
5 Componenti Connesse \(G_{n,p}\)
La seguente definizione è estremamente importante per enuncinare risultati su modelli aleatori: Sia \(\pi_n\) una proprietà che dipende da \(n \in \mathbb{N}\). Diciamo che \(\pi_n\) vale quasi sicuramente, in inglese almost surely (a.s.), se vale la seguente
\[ \lim_{n \to \infty} P(\pi_n) = 1 \]
Al fine di studiare le componenti connesse in un grafo aleatorio generato dal modello di Erdos-Renyi vale il seguente teorema fondamentale, di cui non presenteremo la relativa dimostrazione.
Teorema: Sia \(G_{n, p}\) un grafo generato dal modello di Erdos-Renyi. A seconda dei parametri \(n\) e \(p\), abbiamo i seguenti casi:
Se \(n \cdot p < 1\), allora quasi sicuramente \(G_{n, p}\) non ha componenti connesse con \(> O(\log{n})\) nodi.
Se \(n \cdot p = 1\), allora a.s. \(G_{n, p}\) ha una componente connessa con approssimatamente \(n^{2/3}\) nodi.
Se \(n \cdot p \to c > 1\), allora a.s. esiste una costante \(D > 0\) tale che \(G_{n, p}\) ha una componente connessa con \(\approx n/D\) nodi, e tutte le altre componenti connesse hanno \(< O(\log n)\) nodi.
Se \(p < \frac{(1 - \epsilon)\log n}{n}\), allora a.s. esistono nodi isolati.
Se \(p > \frac{(1 + \epsilon) \log n}{n}\), allora .as. \(G_{n, p}\) è fortemente connesso.
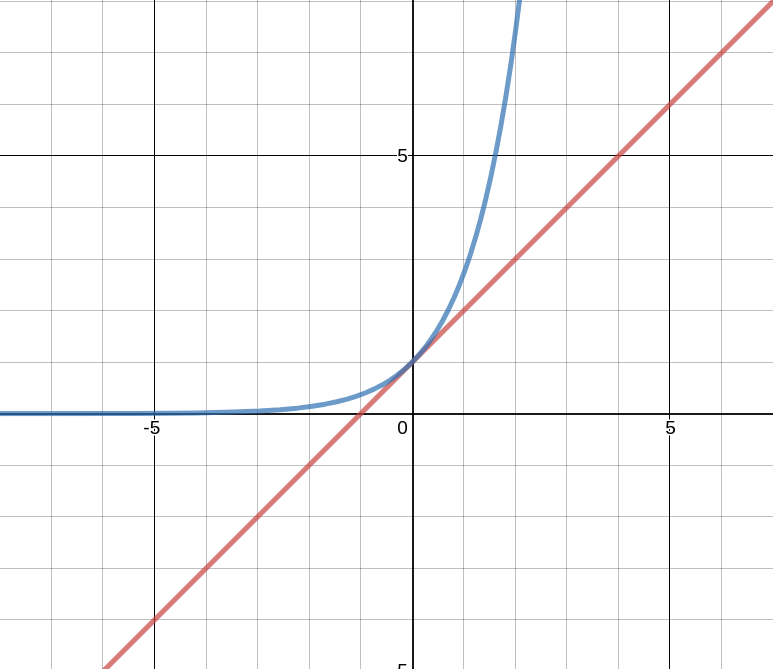
6 Esercizio: \(1 - x \leq e^{-x}\)
Dimostrare la seguente relazione
\[1 - x \leq e^{-x}, \text{ per } x \in \mathbb{R}\]
Andiamo a riportare due dimostrazioni. In particolare dimostriamo la seguente relazione, che è equivalente a quella riportata sopra.
\[1 + x \leq e^{x}, \text{ per } x \in \mathbb{R}\]
6.1 Proof 1
Per \(x < -1\) il caso è banale, in quanto \(e^x > 0 > 1 + x\). Per \(x \geq -1\), utilizziamo la disuguaglianza di Bernoulli, dimostrabile per induzione su \(n\), che ci dice che, dato \(n > 0\) intero e \(y \geq -2\) numero reale, si ha che
\[1 + ny \leq (1 + y)^n\]
In particolare quindi, posto \(y = x/n\), troviamo
\[1 + x \leq (1 + \frac{x}{n})^n\]
Infine, ricordando che \(\lim_{n \to \infty} (1 + x/n)^n = e^x\), troviamo il risultato cercato, ovvero che
\[1 + x \leq (1 + \frac{x}{n})^n \leq \lim_{n \to \infty} (1 + \frac{x}{n})^n = e^x\]
6.2 Proof 2
Notiamo che \(g(x) = x + 1\) è l'espressione della retta tangete al grafico di \(f(x) = e^x\) quando \(x = 0\). Inoltre, abbiamo che \(f(x)\) è una funzione convessa, e quindi il grafico di \(f(x)\) si trova sempre sopra il grafico delle sue retti tangenti. Ma allora,
\[x + 1 = g(x) \leq f(x) = e^x\]
Graficamente,