AR - 02 - Chiusura Triadica

Un esperimento sociale svolto dal sociologo Mark Granovetter ha mostrato come un determinato insieme di persone disoccupate avevano ricevuto le informazioni su possibili lavori vacanti non dai loro amici stretti, ma bensì da conoscenti molto lontani.

La spiegazione data da Granovetter è la seguente: generalmente un dato individuo è già a conoscenza di tutte le informazioni che conoscono i suoi amici più stretti, in quanto c'è più interazione e interesse, mentre ci potrebbe essere una persona conosciuta solamente "alla lontana" che potrebbe avere informazioni utili e ancora non conosciute.

Sulla base di questo adesso andiamo a definire un modello matematico per trattare questa idea fondamentale di differenziare i rapporti in una rete sociale tra rapporti "forti" e rapporti "deboli".

Il primo modello di grafo aleatorio da noi studiato è stato il modello di Erdős-Rényi. La rete generata da questo modello è una rete statica, ovvero una rete che non cambia nel tempo. Alcune volte siamo però interessati a studiare delle reti dinamiche, ovvero delle reti che cambiano nel tempo.

Al fine di studiare la nostra prima rete dinamica introduciamo il grafo \(G=(V, W \cup S)\) delle conoscenze strette e conoscenze deboli. Nel grafo \(G\) infatti gli archi sono divisi in due sottoinsiemi: l'insieme \(S\) delle conoscenze forti (strong), e l'insieme \(W\) delle conoscenze deboli (weak). Intuitivamente la "forza" di una conoscenza può essere pensata come all'importanza di quella particolare conoscenza.

Nello studio di questa tipologia di reti sociali viene utilizzato il seguente principio fondamentale, che prende il nome di chiusura triadica, ed è descritto come segue: Se un nodo \(B\) è collegato tramite un arco di tipo \(S\) a due nodi \(A\) e \(C\), allora ci si può aspettare che, prima o poi, anche \(A\) e \(C\) saranno collegati tra loro da un arco di tipo \(S\). Graficamente,

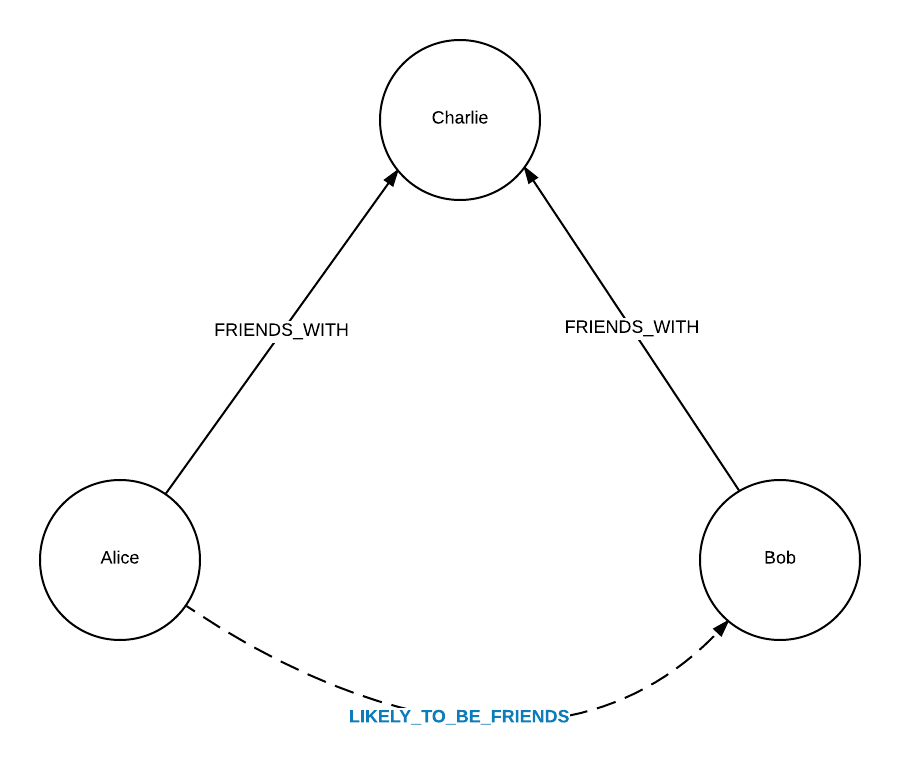
La chiusura triadica è motivita dal fatto che, se \(B\) è un amico stretto sia di \(A\) che di \(C\), allora si potrebbero verificare le seguenti cose:

• \(A\) e \(C\) si potrebbero incontrare, dato che probabilmente escono entrambi molto spesso con \(B\).

• \(A\) e \(C\) potrebbero avere interessi in comune.

• \(A\) e \(C\) potrebbero sviluppare una fiducia reciproca basata sul fatto che \(B\) si fida di entrambi.

dunque notiamo come i triangoli, ovvero triple di nodi collegati da archi a due a due, tendono a chiudersi in presenza di archi forti.

Il coefficiente di clustering è una quantità introdotta nel campo della sociologia ed è utilizzata al fine di stimare quanto un nodo è centrale all'interno del suo vicinato.

Definendo con \(N(u) := \{y \in V: (y, u) \in E\}\) l'insieme dei nodi adiacenti al nodo \(u\), detto anche vicinato di \(u\), troviamo la seguente definizione per il coefficiente di clustering di \(u\):

\[c(u) := \frac{ | \{ (x, y): (x, u) \in E \wedge (y, u) \in E \}| }{ \frac{ |N(u)| \cdot ( |N(u)| - 1)}{2}}\]

Notiamo che nel nominatore troviamo il numero effettivo di triangoli che incidono su \(u\), mentre nel denominatore troviamo il numero massimo di triangoli che possono incidere su \(u\).

Consideriamo il seguente grafico

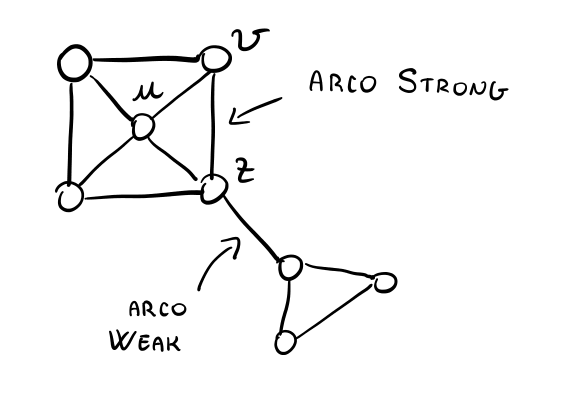
Notiamo che i nodi \(u\) e \(z\) beneficiano della presenza della rete in modo diverso:

• \(u\) si fida dei suoi vicini, ma non vede ciò che è al di fuori della sua cerchia di amici. (+trust, -information).

• \(z\) ottiene più informazioni dalla rete, ma ha meno fiducia. (+information, -trust).

Il principio introdotto prima e chiamato chiusura triadica può essere formalizzato come segue: Il nodo \(u\) ha la strong triadic closure property, abbreviata con STCP, se e solo se

\[\forall x, y: (u, x) \in S \,\, \wedge \,\, (u, y) \in S \implies (x, y) \in W \cup S\]

Un arco è detto bridge se, una volta che viene rimosso, disconnette la rete.

Dato però che in reti molto grandi è difficile trovare archi bridge, siamo interessati a dare una definizione più locale del concetto di bridge. Intuitivamente un local bridge dovrebbe essere un arco che, se dovesse essere rimosso, aumenterebbe la distanza tra i nodi ad esso incidenti. Arriviamo dunque alla seguente definizione di local bridge: Un arco \((a, b)\) è un local bridge, abbreviato LB, se

\[N(a) \cap N(b) = \emptyset\]

Quindi un local bridge è un arco tale che, se rimosso, aumenta di un valore \(> 2\) la distanza tra i nodi ad esso incidenti.

Osservazione: Notiamo che mentre i concetti di archi strong e archi weak sono proprietà locali, ovvero proprietà che pertengono al singolo nodo, il concetto di local bridge è una proprietà globale, in quanto per verificare tale proprietà bisogna analizzare una buona parte della rete.

Al fine di collegare la proprietà locale delle stronk/weak ties e la proprietà globale dei local bridge vale il seguente teorema.

Teorema: Se il nodo \(u\) soddisfa la Strong Triadic Closure Property (STCP) e \(\exists x, y \in N(u) \text{ tali che } (x, u) \in S \,\, \wedge \,\, (y, u) \in S\), allora

\[\forall \text{ LB }(u, z) : (u, z) \in W\]

Proof: Sia \((u, z)\) un local bridge. Dalle assunzioni sappiamo che \((x, u) \in S\) e \((y, u) \in S\). Ma allora \(x\) e \(y\) non sono adiacenti a \(z\), in quanto se lo fossero allora la rimozione di \((u, z)\) non andrebbe ad aumentare la distanza tra i vicini di \(z\), e quindi \((u, z)\) non sarebbe un local bridge.

Ora, se \((u, z)\) fosse un arco forte, ovvero se \((u, z) \in S\), allora, dato che \(u\) soddisfa la STCP, avremmo che

\[\begin{cases} (u, x) \in S \,\, \wedge \,\, (u, z) \in S \implies (x, z) \in S \cup W \\ \\ (u, y) \in S \,\, \wedge \,\, (u, z) \in S \implies (y, z) \in S \cup W \\ \end{cases}\]

e dal paragrafo di prima sappiamo che questo non può succedere, in quanto altrimenti \((u, z)\) non sarebbe un local bridge. Ma allora l'arco \((u, z)\) è necessariamente un arco debole.

\[\tag*{$\blacksquare$}\]

Osservazione: Notiamo che entrambe le ipotesi sono necessarie per ottenere il risultato del teorema. Infatti, nelle ipotesi del teorema la seconda condizione, ovvero la richiesta che \(\exists x, y \in N(u) \text{ tali che } (x, u) \in S \,\, \wedge \,\, (y, u) \in S\), è aggiunta per evitare nodi \(u\) che soddisfano la STCP in modo banale, ovvero nodi che non hanno almeno due legami forti. In particolare necessito la presenza del nodo \(y\) in quanto altrimenti l'arco \((u, x)\) potrebbe essere un LB, e dunque il teorema non vale. La presenza del nodo \(y\), unita al fatto che \(u\) gode della proprietà STCP, impedisce a \((u, x)\) di essere un LB.

In questo nuovo modello più alto è il peso di una relazione e più la relazione è importante. In particolare, più è alto il peso degli archi e più mi aspetto che si verifichi la STCP (rilassamento visione locale).

Al fine di rilassare la visione globale dei LB si introduce il seguente coefficiente: dati \((u, v) \in E\), il neighborhood overlap tra \(u\) e \(v\) è definito come segue,

\[NO(u, v) := \frac{ |N(u) \cap N(v) | }{ | N(u) \cup N(v) - \{u, v\} | }\]

Notiamo che \(NO(u, v)\) è il rapporto tra i vicini in comune e i vicini in totale.

Dalla definizione di LB segue che se \((u, v)\) è LB, allora \(NO(u, v) = 0\). Inoltre in questo nuovo modello rilassato si spera che più \(NO(u, v)\) è basso, e più l'arco \((u, v)\) è un LB. Dunque il neighborhood overlap è il rilassamento della proprietà globale del LB.

La congettura secondo la quale più \(NO(u, v)\) è basso, e più l'arco \((u, v)\) è un LB è stata confermata sperimentalmente da un esperimento fatto da Omnela.

Studiando una rete cellulare, e pesando le relazioni rispetto alla durata complessiva delle chiamate, è stato verificato che più basso era il coefficiente di neighborhood overlap tra due nodi \(u\) e \(v\), e in modo più frequente la rimozione dell'arco \((u, v)\) rendeva la rete più disconnessa.