AR - 03 - Partizionamento in Comunità I

Lecture Info

Data: [2018-10-22 lun]
Introduzione: In questa lezione abbiamo introdotto lo studio delle comunità, definendo in vari modi cosa si intende per "comunità" in una rete sociale. A tale fine sono state riportate alcune nozioni di teoria della complessità.

1 Gruppi Coesi (Zachary)

In un famoso esperimento chiamato "An information flow model for conflict and fission in small groups", il ricercatore Zachary ha studiato una rete sociale formata da persone che partecipavano ad un gruppo di Karate.

Dopo una faida avvenuta tra il maestro del gruppo e un allievo, il gruppo si è diviso in due sottogruppi. Zachary quindi si è posto la seguente domanda: che tipo di informazioni mi può dare la struttura della rete rispetto ai gruppi di persone che vanno più d'accordo tra loro?

Notiamo subito che non ci possiamo basare semplicemente sui local bridge per individuare questi "gruppi coesi", in quanto individui collegati da local bridge potrebbero comunque far parte dello stesso "gruppo coeso". Dobbiamo quindi trovare una buona definizione che ci permetta di rappresentare il concetto intuitivo di "gruppo coeso", che da questo momento in poi chiameremo sempre comunità.

Al fine di trattare il problema della ricerca delle comunità in una rete sociale dobbiamo però prima ricordare alcune nozioni riprese dalla teoria della complessità.

2 Teoria della Complessità

La teoria della complessità studia la difficoltà intrinseca dei problemi.

Dato un problema, la sua complessità coincide con la complessità dell'algoritmo più efficiente che risolve il problema. La complessità di un algoritmo a sua volta è la quantità di risorse, come ad esempio il tempo di calcolo (complessità temporale), o quantità di memoria (complessità spaziale), necessarie al fine di eseguire l'algoritmo fino alla terminazione con un dato input.

L'obiettivo ultimale della teoria della complessità è quindi lo studio della complessità degli algoritmi in funzione della dimensione dell'input $x$, che indichiamo con $|x|$, e che indica il numero di celle di memoria utilizzate dal modello di calcolo su cui esegue l'algoritmo al fine di memorizzare l'input.

2.1 Problemi Decisionali

I primi problemi studiati dalla teoria della complessità sono i cosiddetti problemi decisionali. Un problema decisionale è caretterizzato dalle seguenti cose:

Un insieme di istanze.
Un insieme di possibili soluzioni per una data istanza.
Una serie di condizioni che devono essere soddisfatte da una potenziale soluzione al fine di risolvere il problema.

2.2 P vs NP

Al fine di confrontare la complessità di vari problemi sono state introdotte delle classi di complessità. Le classi di complessità più famose sono la classe P e la classe NP, definite come segue:

La classe P contiene i problemi che sono trattabili computazionalmente, ovvero i problemi che sono decisi da un algoritmo la cui esecuzione su input $x$ richiede un tempo polinomiale in $|x|$. Ordinare una lista è un esempio di problema in P
La classe NP contiene i problemi che sono risolvibili in un tempo non-deterministico polinomiale. Il concetto di computazione non-deterministica fa riferimento ad una classe di algoritmi più potenti di quelli che possono essere eseguiti utilizzando il modello standard di Von Neumann. Intuitivamente i problemi in NP sono problemi per cui esiste un modo per controllare se possibile soluzione è valida (chiamato anche un certificato per l'istanza) in un tempo deterministico polinomiale. Fattorizzare un numero nei suoi fattori primi è un esempio di problema in NP.

Non tutti i problemi si trovano in P o in NP. Il problema di fare la mossa migliore in una partita di scacchi ad esempio non è un problema in NP, in quanto la lunghezza di una possibile soluzione, ovvero di un possibile certificato, non è polinomiale rispetto all'input, e dunque non può essere controllata in tempo polinomiale.

Notiamo infine che non tutti i problemi in NP sono necessariamente "difficili". Infatti

\[\textbf{P} \subseteq \textbf{NP}\]

e non si è ancora dimostrato che P $\neq$ NP. Dunque è più giusto dire che i problemi in NP sono i problemi "sicuramente non troppo difficili".

2.3 NP-Completezza

Anche se è facile dimostrare che P $\subseteq$ NP, dimostrare il fatto che P è strettamentamente contenuto in NP è uno dei problemi aperti più importanti nel campo dell'informatica teoria. Al fine di individuare quei problemi che si potrebbero trovare in NP $-$ P è stato introdotto il concetto di NP-completezza, che a sua volta fa riferimento al concetto di riduzione polinomiale.

Definizione: Un problema $A$ è detto riducibile polinomialmente ad un problema $B$, quando ogni istanza $x$ di $A$ è trasformabile, in tempo polinomiale, tramite una funzione $f:A \to B$, in una istanza $y = f(x)$ di $B$ tale che

\[x \text{ è soluzione di } A \iff y \text{ è soluzione di } B\]

Se $A$ è riducibile polinomialmente a $B$ allora scriviamo $A \preceq B$.

Notiamo che la riduzione polinomiale può essere utilizzata come una strategia risolutiva per un dato problema. Infatti, se so risolvere il problema $B$, e conosco una riduzione polinomiale $f$ da $A$ a $B$, allora posso anche risolvere il problema $A$ procedendo come segue:

Mi calcolo $f(x)$
Risolvo $f(x)$ utilizzando l'algoritmo che conosco per $B$. Se $f(x)$ risolve $B$, allora $x$ risolve $A$ e viceversa.

La riduzione polinomiale può anche essere utilizzata come tecnica per dimostrare che un dato problema è difficile da risolvere utilizzando il concetto di NP-completezza, riportato a seguire

Definizione: Un problema decisionale $A$ è NP-C, o NP-completo, se valgono le seguenti cose:

$A \in \textbf{NP}$
$\forall B \in \textbf{NP} : [B \preceq A]$

In altre parole, se ho un problema $A$ che so di essere NP-C, allora qualsiasi altro problema $B$ in NP può essere ridotto al problema $A$, e quindi se risolvo $A$ in tempo polinomiale sono in grado anche di risolvere tutti i problemi di NP in tempo polinomiale, ovvero avrei che NP $=$ P.

Da un punto di vista pratico, se vogliamo dimostrare che un problema $A$ è "difficile", allora possiamo prendere un problema $B$ che sappiamo già essere NP-C e ridurre $B$ ad $A$. Così facendo infatti abbiamo dimostrato che $A$ è a sua volta un problema NP-C.

3 Comunità

Sia $G=(V, E)$ un grafo, vogliamo partizionare $V$ in due sottoinsiemi $V_1, V_2$, tali che

$V_1 \cap V_2 = \emptyset$
$V_1 \cup V_2 = V$.

A seguire due possibli definizione di comunità:

3.1 Web-Community (WC)

$V_1$ è una weak web-community se

\[\forall u \in V_1: \,\, | N(u) \cap V_1 | \geq | N(u) \setminus V_1 |\]

Quindi $V_1$ è una weak web-community se per ogni nodo $u$ in $V_1$, il numero di vicini di $u$ che sono in $V_1$ sono maggiori rispetto al numero dei vicini di $u$ che non sono in $V_1$.

3.2 Cut-Community (CC)

$V_1$ è una cut-community se

\[| \{ (u, v) \in E: u \in V_1 \,\, \wedge \,\, v \in V \setminus V_1\} | = \min{ | \{ (u, v) \in E: u \in V_1 \,\, \wedge \,\, v \in V \setminus V_1 \} | : V_1 \subseteq V } |\]

Quindi $V_1$ è una cut-community se e solo se $V_1$ è un taglio minimo del grafo.

3.3 Connessione tra WC e CC

Il seguente risultato collega le due definizioni:

Proposizione: Sia $G(V, E)$ un grafo, e sia $C \subseteq V$ una cut-community tale che $|C| > 1$ e $| V \setminus C | > 1$. Allora $\langle C, V \setminus C \rangle$ è una partizione di $G$ in due web-communities.

Proof: Supponiamo, per assurdo, che $C$ non è una web-community. Allora esiste un $u \in C$ tale che

\[| N(u) \cap C | \leq | N(u) \setminus C |\]

Consideriamo ora $C' := C \setminus \{u\}$. Dalle ipotesi segue che $C' \neq \emptyset$. Notiamo inoltre che

\[\begin{split} \lvert \{(x, y): &x \in C' \,\, \wedge \,\, y \in V \setminus C'\} \rvert = \\ &= | \{(x, y): x \in C \,\, \wedge \,\, y \in V \setminus C\}| - |\{(u, y): y \not \in C\} | + |\{(u, y): y \in C\}| \\ &= | \{(x, y): x \in C \,\, \wedge \,\, y \in V \setminus C\}| - |N(u) \setminus C| + |N(u) \cap C | \\ &\leq | \{(x, y): x \in C \,\, \wedge \,\, y \in V \setminus C\}| \\ \end{split}\]

Ma allora $C$ non è una cut-community, il che ci porta ad un assurdo. Dunque $C$ deve necessariamente esserer una web community.

Al fine di completare la dimostrazione basta ripetere il ragionamento appena svolto per l'insieme $V \setminus C$.

\[\tag*{$\blacksquare$}\]

Osservazione: Questa relazione tra le cut-communities e le web-communities è molto utile, in quanto esistono algoritmi che calcolano il min-cut in tempo polinomiale su grafi pesati con pesi interi. Detto questo, nella proposizione c'è la richiesta che la cut-community deve essere tale che $|C| > 1$ e $| V \setminus C |$. Tale condizione non è sempre verificata, e dunque non è detto che il taglio minimo soddisfa tale richiesta. Detto altrimenti, avere una cut-community non ci porta immediatamente ad una web-community, come mostra il seguente contro-esempio:

3.4 Esempio: CC senza WC

In questo grafo $G=(V, E)$, abbiamo che i vertici sono dati da $V = \{u_0, u_1, u_2, u_3, u_4\} \cup \{v_0, v_1, v_2, v_3, v_4\}$, mentre gli archi sono dati da

$\forall i, j: \,\, (u_i, u_j) \in E$, (clique di sopra)
$\forall i, j: \,\, (v_i, v_j) \in E$, (clique di sotto)
$\forall i: \,\, (u_i, v_{i+1}), (u_i, v_{i+2}), (u_i, v_{i+3})$, (collegamenti tra clique)

Il grafo può essere disegnato nel seguente modo

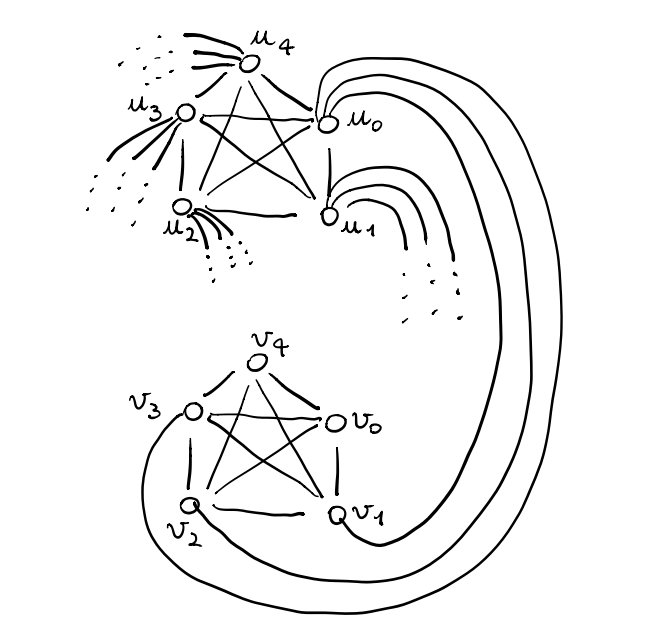
Notiamo che ogni nodo ha grado $7$. Inoltre il taglio che isola un nodo ha dimensione $7$, mentre ogni altro taglio ha dimensione $\geq 7$. Dunque in questo esempio notiamo che semplicemente calcolando il cut-minimo ciò non ci permette di ottenere una web-community.