AR - 04 - Partizionamento in Comunità II
Lecture Info
Data:
Introduzione: In questa lezione abbiamo dimostrato che il problema di partizionare un grafo in due (strong)-web communities è un problema NP-hard. Infine, abbiamo introdotto il concetto di (edge)-betweenness, e lo abbiamo studiato per calcolare le comunità di un grafo tramite il metodo di Girvan-Newman.
1 WCP Problem
Il problema WCP, che sta per WebCommunitiesPartition, chiede la seguente cosa: dato un grafo \(G=(V, E)\), esiste una partizione \(\langle V_1, V_2 \rangle\) di \(V\) in due (strong) web communities? Andiamo adesso a dimostrare che tale problema è un problema NP-completo.
Per prima cosa facciamo vedere che WCP è un problema in NP. A tale fine notiamo che un certificato per tale problema è una partizione \(\langle V_1, V_2 \rangle\) di \(V\). Per controllare il certificato possiamo procedere come segue:
Verifica che \(\langle V_1, V_2 \rangle\) è una partizione di \(V\)
\(\forall u \in V1\)
calcola \(|N(u) \cap V_1|\)
calcola \(|N(u) \setminus V_1|\)
controlla che \(|N(u) \cap V_1| \geq |N(u) \setminus V_1|\)
Ripetere il punto precedente per ogni \(u \in V2\)
Il numero di passi necessari per controllare il certificato è quindi dell'ordine di \(O(|V|^2(|V|+|E|))\), ovvero è polinomiale rispetto alla lunghezza dell'input. Dunque WCP \(\in\) NP.
Mostriamo adesso che WCP è un problema NP-completo riportando una riduzione dal problema 3-SAT.
1.1 3-Sat \(\preceq\) WCP
Ricordiamo che il problema 3-SAT prende in input una formula booleana in forma 3-CNF, ovvero formata da una congiunzione di clausole in cui ciascuna clausola è una disgiunzione di letterali, e si chiede se esiste o meno una assegnazione di verità che soddisfa la formula.
Volendo formalizzare, sia \(I = \langle f, X \rangle\) una istanza di 3-SAT, con \(X = \{x_1, x_2, ..., x_n\}\) insieme delle variabili e \(f = C_1 \land ... \land C_2\) funzione booleana in 3-CNF, con \(C_i = ( l_{i,1} \lor l_{i, 2} \lor l_{i, 3})\) clausola di letterali. In altre parole,
\[f = (l_{1, 1} \lor l_{1, 2} \lor l_{1, 3}) \land (l_{2, 1} \lor l_{2, 2} \lor l_{2, 3}) \land ... \land (l_{m, 1} \lor l_{m, 2} \lor l_{m, 3})\]
L'idea alla base della riduzione è quella di utilizzare la formula \(f\) per costruire un grafo. Il grafo sarà costruito in modo tale da poter essere partizionato in due (strong)-web communities nel caso in cui la formula sia soddisfacibile. A ciascuna partizione è poi associato un valore di verità (True o False).
Andiamo quindi a descrivere il modo in cui costruiamo il grafo a partire da \(f\).
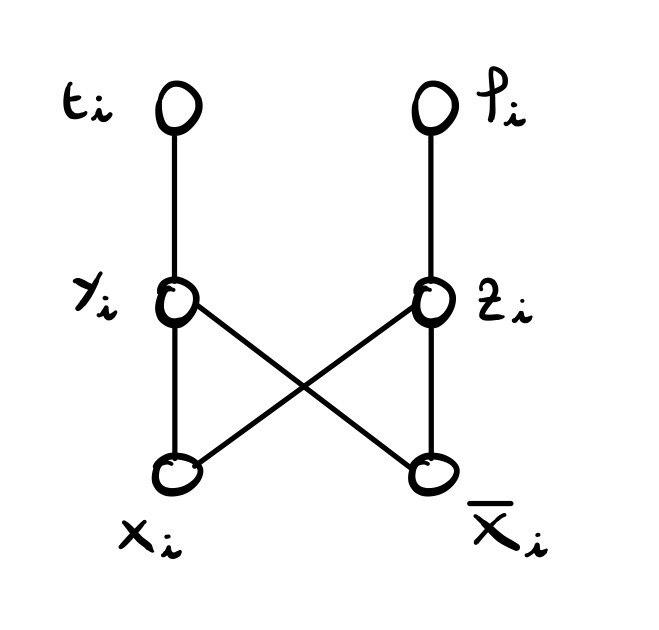
1.1.1 Variable Gadget
Ad ogni variabile \(x_i\) è associato il seguente pezzo di grafo
1.1.2 Nodi T e F
Si introducono poi due nodi speciali, chiamati \(T\) e \(F\). La partizione a cui appartiene il nodo \(T\) sarà associata al valore di verità True, mentre quela a cui appartiene il nodo \(F\) sarà associata al valore di verità False.
Per fare questo si collega il nodo \(T\) a tutti i nodi \(t_i\), e \(F\) a tutti i nodi \(f_i\), ottendo quindi il seguente grafo
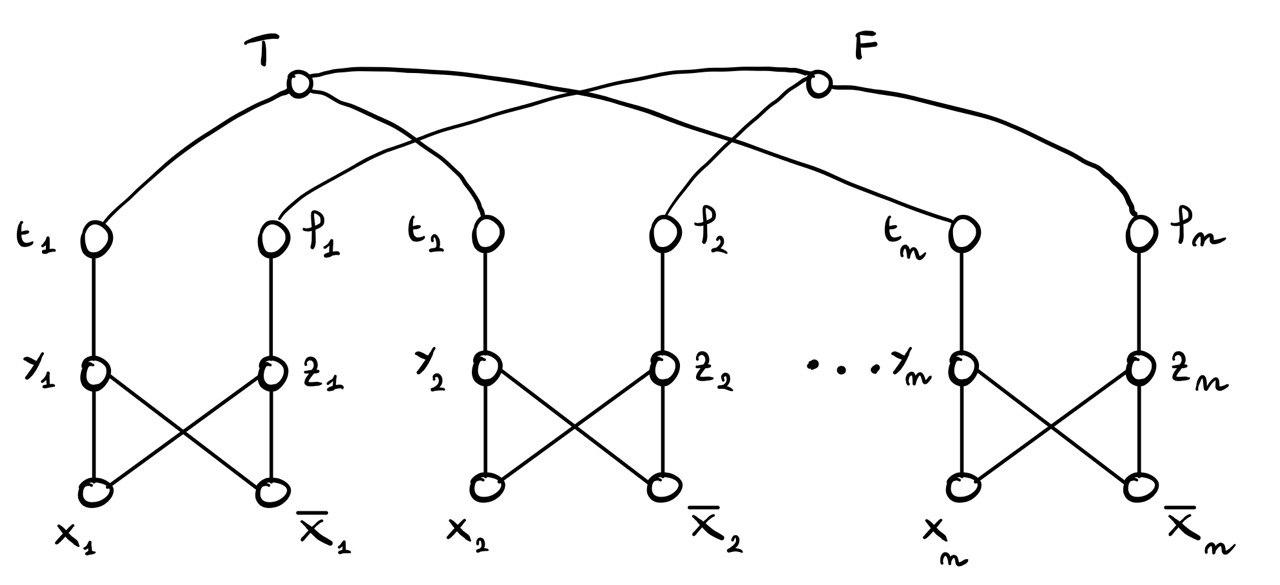
Notiamo che con questa costruzione abbiamo che \(x_i\) e \(\bar{x}_i\) non si possono trovare nella stessa partizione per avere due (strong)-web communities. Infatti, se ad esempio \(x_1\) e \(\bar{x}_1\) stanno in \(V_1\), allora \(z_1 \in V_1\), e quindi \(f_1\) non potrebbe stare né in \(V_1\) né in \(V_2\). Dunque, se \(x_1 \in V_1\), allora \(\bar{x}_1 \in V_2\) e viceversa.
1.1.3 Clause Gadget
Ogni clausola della formula diventa un nodo del grafo. Tale nodo è poi adiacente ai nodi associati letterali contenuti nella clausola e presenti nei gadget associati alle variabili introdotti prima.
Inoltre, per legare il ritrovamento delle 2 (strong)-web communities alla soddisfacibilità della formula \(f\), si introducono, per ogni clausola \(C_i\), tre nodi formali chiamati \(l_{i,1}, l_{i,2}, l_{i,3}\). Questi nodi sono collegati alla clausola \(C_i\) e al nodo \(T\), e il loro compito è far si che almeno un letterale presente in \(C_i\) faccia parte della partizione associata al valore di verità \(T\) nel caso in cui si riesca a trovare un partizionamento dei nodi del grafo in due (strong)-web communities.
Ad esempio, se \(C_1 = (x_1 \lor \neg x_2 \lor x_n)\), allora il grafo ottenuto è il seguente
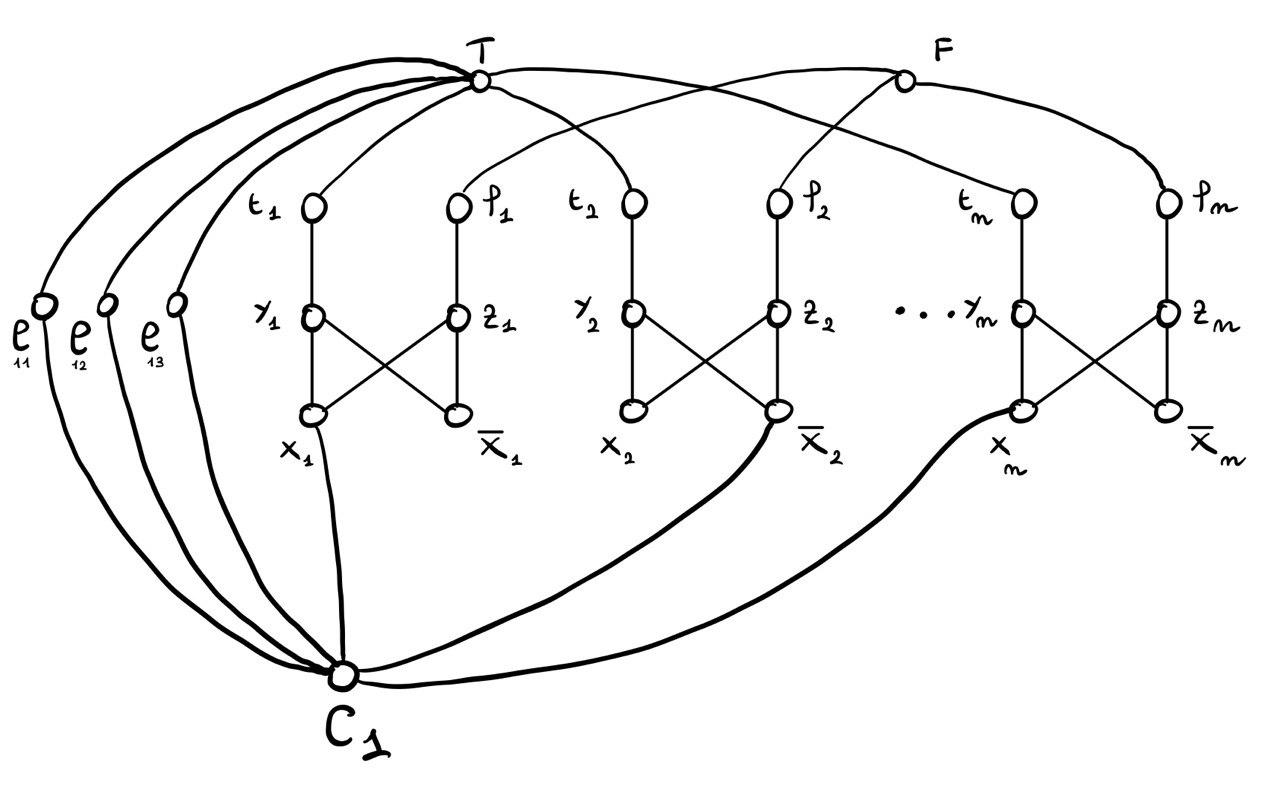
1.1.4 Ultimo Ritocco
Notiamo che con l'aggiunta dei gadget per le clausole abbiamo aumentato il numero di vicini nella partizione di \(T\) dei letterali che appaiono in molte clausole. Questo potrebbe limitare la scelta del letterale di appartenere alla partizione \(F\).
Per togliere questa limitazione l'idea è quella di aggiungere dei nodi formali che veranno poi assegnati alla partizione \(T\) o \(F\) a seconda della partizione a cui il letterale vuole appartenere.
La costruzione finale è quindi la seguente
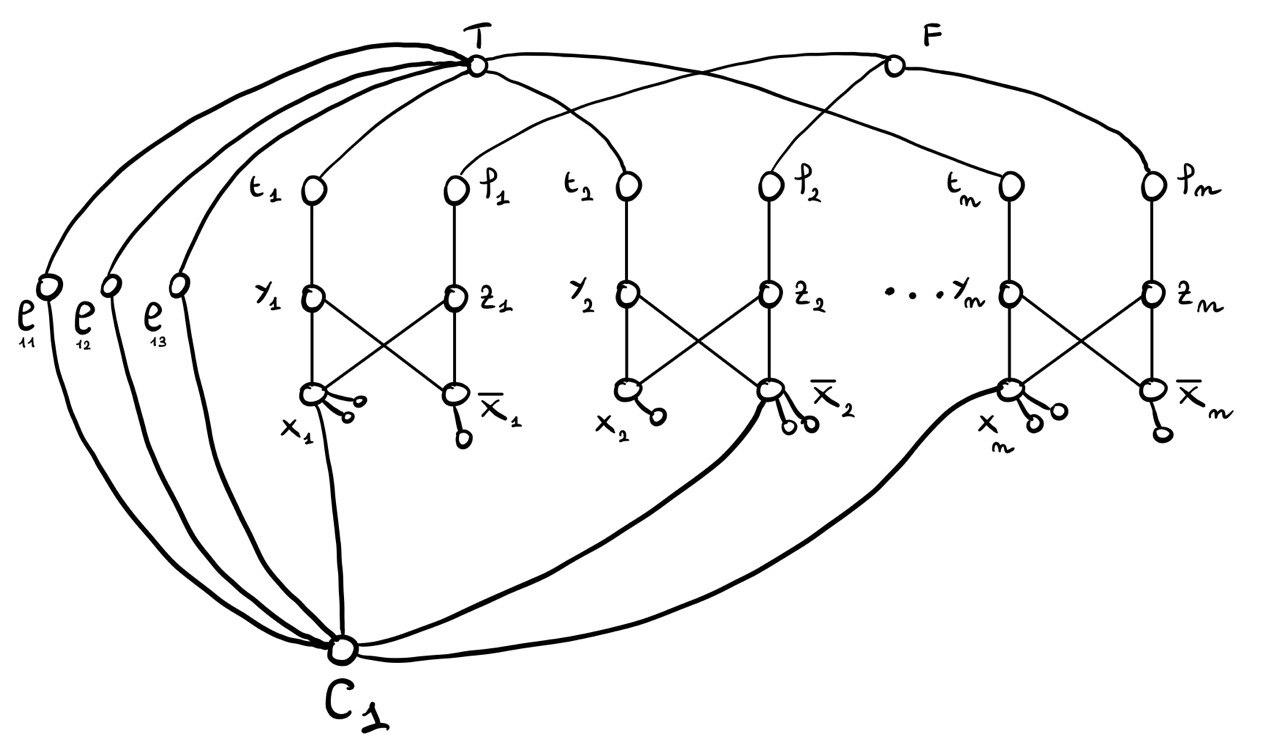
1.1.5 Dimostrazione
Siamo adesso pronti per dimostrare formalmente la riduzione. Procediamo quindi dimostrando entrambi i lati della riduzione
\((\Rightarrow)\): Sia \(f\) soddisfacibile, e sia \(a(\cdot)\) una assegnazione di verità che soddisfa \(f\).
Una volta che abbiamo costruito il grafo come descritto in precedenza, possiamo costruire una partizione di \(V\) nel seguente modo:
Le variaibli a cui \(a(\cdot)\) assegna il valore True le metto nella partizione di \(T\).
Le variaibli a cui \(a(\cdot)\) assegna il valore False le metto nella partizione di \(F\).
Dato che \(a(\cdot)\) soddisfa la formula \(f\) posso mettere i nodi \(c_i\) nella partizione \(T\) senza perdere i requisiti di avere due (strong)-web communities.
Ai nodi associati alle variabili assegno la stessa partizione della variabile.
In questo modo ho trovato due partizioni, che per costruzione sono delle (strong)-web communities.
\((\Leftarrow)\): Viceversa, supponiamo di aver partizionato \(V\) in due (strong)-web communities \(V_1\) e \(V_2\), e supponiamo che \(T \in V_1\) e \(F \in V_2\). Allora definisco la seguente assegnazione di verità \(a(\cdot)\):
Se \(x_i \in V_1\), allora \(a(x_i) = \text{True}\)
Se \(x_i \in V_2\), allora \(a(x_i) = \text{False}\)
Argomentiamo adesso che \(a(\cdot)\) soddisfa \(f\). Questo segue dal fatto che, per avere che \(V_1\) e \(V_2\) siano due (strong)-web communities, dobbiamo avere che per ogni clausola \(C_i\), \(C_i \in T\), e quindi che esiste almeno letterale presente in \(C_i\) e contenuto nella partizione di \(T\). Ma allora questo letterale verrà reso vero dall'assegnazione di verità, soddisfando la clausola \(C_i\). Dato che questo vale per ogni clausola della formula \(f\), ne consegue che \(a(\cdot)\) soddisfa la formula \(f\).
\[\tag*{$\blacksquare$}\]
2 (Edge)-Betweenness
Avendo appena dimostrato che il concetto intuitivo di web-communities è computazionalmente intrattabile, necessitiamo di un nuovo criterio al fine di identificare le nostre comunità.
Un possibile nuovo approccio è il seguente: al fine di identificare le comunità nella rete utilizziamo gli archi in cui passa più informazione. A tale fine introduciamo il concetto di "centralità" (o betweenness) per un arco.
Definizione: la (edge)-betweenness di un arco \((u, v)\) in un grafo \(G\) è definita come segue
\[b(u, v) := \frac{1}{2} \cdot \sum\limits_{\substack{s, t \in V: \\ s \neq t}}\frac{ \text{# shortest paths in $G$ da $s$ a $t$ che attraversano l'arco $(u, v)$} }{ \text{# shortest paths in $G$ da $s$ a $t$}}\]
Osservazione: Notiamo che al fine di utilizzare il concetto di (edge)-betweenness per identificare le comunità assumiamo implicitamente che l'informazione nella rete che stiamo studiando viaggia attraverso le shortest paths. Sotto questa ipotesi quindi il valore \(b(u, v)\) rappresenta quanta informazione passa nell'arco \((u, v)\).
Andando a definire \(\sigma_{s,t}(u, v)\) come il numero di shortest paths da \(s\) a \(t\) che passano attraverso l'arco \((u, v)\), e \(\sigma_{s, t}\) come il numero di shortest paths da \(s\) a \(t\), possiamo riscrivere \(b(u, v)\) nel seguente modo:
\[b(u, v) := \frac{1}{2} \sum\limits_{\substack{s, t \in V: \\ s \neq t}} \frac{\sigma_{s,t}(u, v)}{\sigma_{s, t}}\]
Dato che però le shortest paths in un grafo possono essere in numero esponenziale rispetto alla dimensione del grafo, necessitiamo di un metodo per contarle senza doverle necessariamente enumerare tutte.
2.1 Calcolo di \(b(u, v)\)
Il metodo riportato a seguire è stato scoperto da Girvan e Newman.
Si inizia definendo il seguente termine
\[\forall s \in V: \,\,\, b_s(u, v) := \sum_{t \in V \setminus \{s\}} \frac{\sigma_{s,t}(u, v)}{\sigma_{s, t}}\]
Così facendo, una volta che sappiamo calcolare \(b_s(u, v)\) per ogni \(s \in V\), possiamo anche calcolare la betweenness tra \(u\) e \(v\) nel seguente modo
\[b(u, v) = \frac{1}{2} \sum_{s \in V} b_s(u, v)\]
L'algoritmo che calcola \(b_s(u, v)\) dopo aver fissato \(s \in V\) procede in tre passi:
1 - BFS su \(s\)
Il primo passo consiste nell'eseguire una visita BFS (Breadth First Search) partendo dal nodo \(s\) sul grafo \(G\) per ottenere l'albero di visita \(T_s\).
2 - Calcolo \(\sigma_{s, u}\) per ogni \(u \in V\)
Siano \(V_1, V2, ..., V_d\) i sottoinsiemi di \(V\) in base alla loro distanza da \(s\), dove con \(d\) indichiamo l'altezza dell'albero \(T_s\) calcolato prima. Notiamo che questi sottoinsiemi sono facilmente costruibili a partire dall'albero \(T_s\).
Il secondo passo consiste nel calcolare il valore di \(\sigma_{s, u}\) per ogni \(u \in V\) nel seguente modo:
\(\forall u \in V_1: \sigma_{s, u} = 1\)
\(\forall u \in V_i: \sigma_{s, u} = \sum\limits_{\substack{v \in V_{i-1}:\\ (v, u) \in E}} \,\, \sigma_{s, v}\)
3: Procedimento bottom-up
In questo passo simuliamo l'invio di una unità di informazione dal nodo \(s\) a tutti i nodi della rete. Definiamo quindi i seguenti termini:
\(\forall v \in V: \,\, f_s^v\) indica il flusso da \(s\) a \(v\).
\(\forall (u, v) \in E: \,\, f_s(u, v)\) indica il flusso da \(s\) passante per l'arco \((u, v)\).
Notiamo che i nodi \(t\) appartenenti all'ultimo livello ricevono solamente \(1\) unità di informazione. Invece, Per quanto riguarda gli archi entranti nell'ultimo livello, ovvero della forma \((v, t)\) con \(v \in V_{d-1}\), abbiamo che ciascun arco poterà una frazione del flusso che deve arrivare a \(t\). In particolare quindi l'arco \((v, t)\) porterà la frazione \(\sigma_{s, v} / \sigma_{s, t}\) di flusso, in quanto tale frazione rappresenta proprio la frazione degli shortest paths che vanno da \(s\) a \(t\) e che passano per \(v\). Inizialmente troviamo quindi la seguente situazione per il caso base:
\[\begin{cases} \forall t \in V_d&: f_s^t = 1 \\ \forall v \in V_{d-1}, \forall t \in V_d&: f_s(v, t) = 1 \cdot \frac{\sigma_{s,v}}{\sigma_{s,t}} \\ \end{cases}\]
Supponiamo adesso di aver calcolato sia il valore del flusso \(f_s^t\) per ogni nodo \(t \in V_{i+1}\) e sia il flusso entrante su ogni arco che collega il livello \(V_i\) al livello \(V_{i+1}\). Notiamo che con questa conoscenza siamo anche in grado di calcolare il flusso su ogni nodo \(u \in V_i\) e il flusso su ogni arco che collega \(V_{i-1}\) a \(V_{i}\). Infatti, per quanto riguarda il flusso passante per i nodi, abbiamo che
\[\forall u \in V_{i}: \,\,\,\, f_s^u = 1 \,\, + \sum\limits_{\substack{v \in V_i+1: \\ (u, v) \in E}} f_s(u, v)\]
Per quanto riguarda il flusso passante per gli archi troviamo che
\[\forall (u, v) \in E: u \in V_{i-1}, v \in V_{i}, \,\,\,\,\,\, f_s(u, v) = f_s^v \cdot \frac{\sigma_{s,u}}{\sigma_{s,v}}\]
Arrivati a questo punto ci basta notare che
\[f_s(u, v) = b_s(u, v)\]
Quindi, al variare di \(s\), tramite questa simulazione di invio di informazioni a partire da \(s\) siamo in grado di calcolare i vari \(b_s(u, v)\), che possono poi essere utilizzati a loro volta per calcolare la edge-between di ogni arco.
2.2 Girvan-Newman Algorithm
Notiamo che tanto più è elevata la betweenness di un arco e tanto più è elevata l'informazione passante su quell'arco. Notiamo poi che tanta più informazione passa in un arco e tanto più quell'arco si avvicina ad essere un bridge o un local-bridge.
L'idea che hanno avuto Girvan e Newmann è la seguente: si calcola la betweenness per ogni arco e si comincia a togliere dal grafo gli archi con la più alta betweenness finché il grafo si sconnette. I due pezzi del grafo rimanenti saranno quindi le nostre due comunità ricercate.
A seguire riportiamo un frammento del codice python presente nel file edge_betweenness.py, in cui è possibile trovare anche una implementazione in python del calcolo della edge_betwenness.
# partition graph using girvan newman betwenness centrality measure. def girvan_newman(G): connected = is_graph_connected(G) # graph is already disconnected, no need to partition it if not connected: return G # iterate over all edges of the graph to compute the # edge_betweenness betweenness_value = {} for u in G: for v in G[u]: betweenness_value[(u, v)] = edge_betwenness(G, u, v) # start removing edges with highest edge-betweenness until graph # disconnects while connected: # find edge with max betweenness value max_edge = max(betweenness_value, key=betweenness_value.get) u, v = max_edge # remove edge from graph G[u].remove(v) G[v].remove(u) # remove edge from betweennes dictionary betweenness_value.pop(max_edge, None) # check if graph is still connected connected = is_graph_connected(G) return G
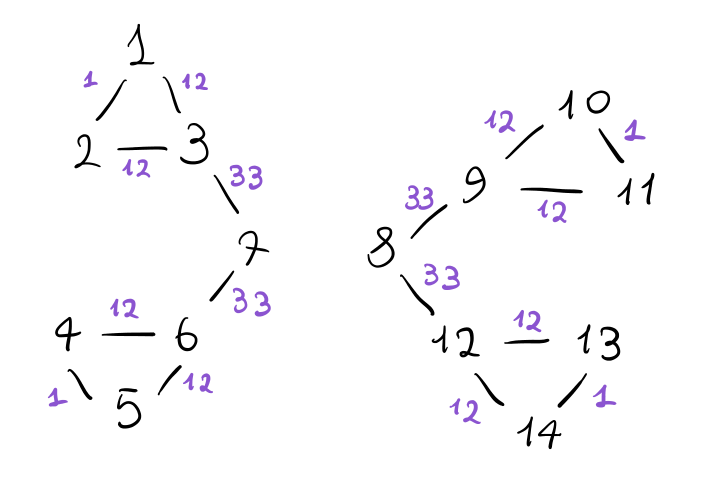
2.2.1 Example
Consideriamo il seguente grafo
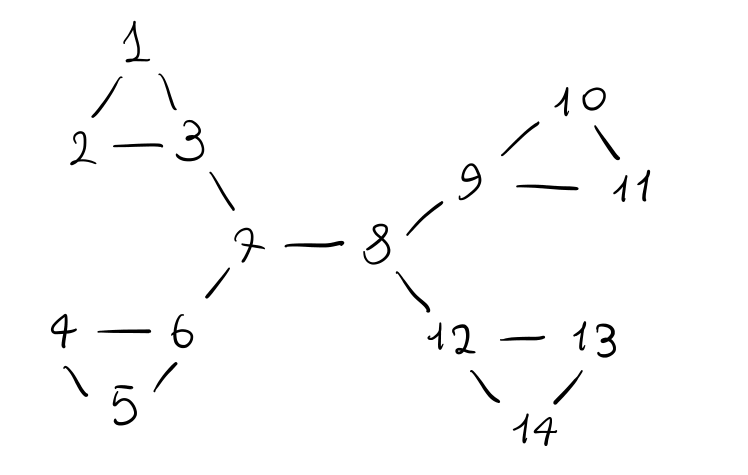
Utilizzando il codice indicato in precedenza, possiamo calcolare il valore della edge-betweenness di ogni arco, per ottenere la seguente situazione
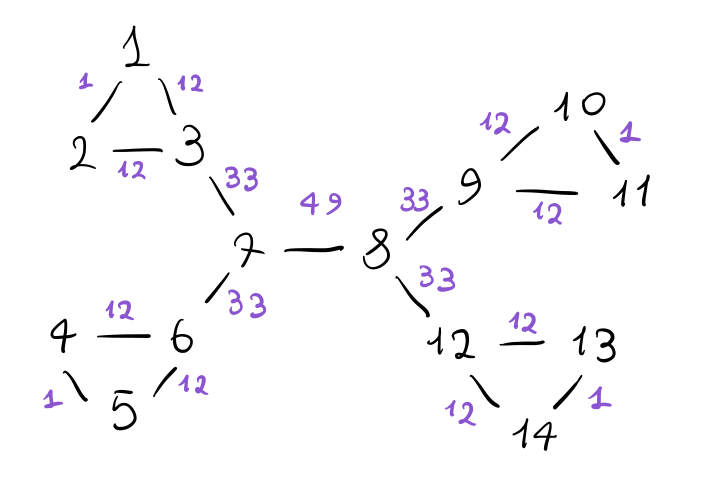
Cominciamo poi ad eliminare gli archi con la edge-betweenness più alta. Alla fine ci fermiamo quando il grafo si disconnette, trovando le seguenti due comunità