AR - 05 - Stabilità in Reti Segnate I
Lecture Info
Data:
Capitolo Libro: Chapter 5 - Positive and Negative Relationships
Introduzione: In questa lezione abbiamo iniziato lo studio della stabilità in una rete segnata, introducendo il modello matematico delle reti segnati con alcune importanti definizioni, che sono state analizzate e caratterizzate nel corso della lezione.
1 Omofilia
Nel contesto delle reti sociali, con il termine omofilia si intende la tendenza degli individui nell'associarsi e nel creare legami con altri individui considerati simili rispetto a determinate caratteristiche.
Le dinamiche che portano alla creazione e all'evoluzione di una rete sociale sono quindi le seguenti:
Omofilia: In modo spontaneo i nodi della rete selezionano altri nodi ad essi simili;
Influenza della rete: Una volta strutturata, la rete tende ad incentivare la creazione di determinate relazioni.
2 Reti Segnate (complete)
Siamo interessati a modellare reti sociali in cui le relazioni possono essere di due tipologie:
Relazioni di amicizia
Relazioni di inimicizia
Per fare questo un possibile approccio è quello di utilizzare un grafo \(G\) in cui gli archi sono etichettati con due particolari etichette, a seconda della natura della relazione rappresentata dall'arco. Graficamente otteniamo il seguente oggetto
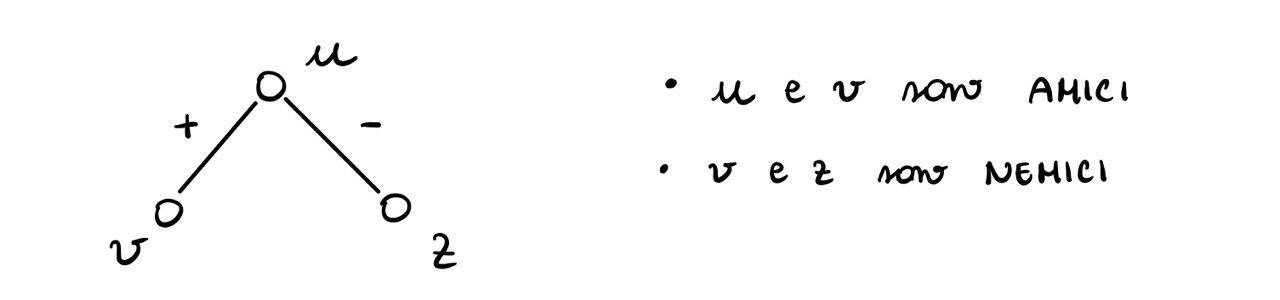
Intuitivamente si capisce che le informazioni in una rete segnata si diffondono in modo diverso a seconda del tipo di arco. In particolare le informazioni sono più propense a passare per archi associati all'amicizia piuttosto che archi associati a nodi nemici tra loro.
2.1 Stabilità in Reti Segnate
Per studiare il concetto di stabilità in una rete segnata sono state studiate le possibili configurazioni in cui i triangoli della rete si possono trovare.
Alcune configurazioni considerate strutture stabili sono,
Il triangolo in cui tutti sono amici con tutti.
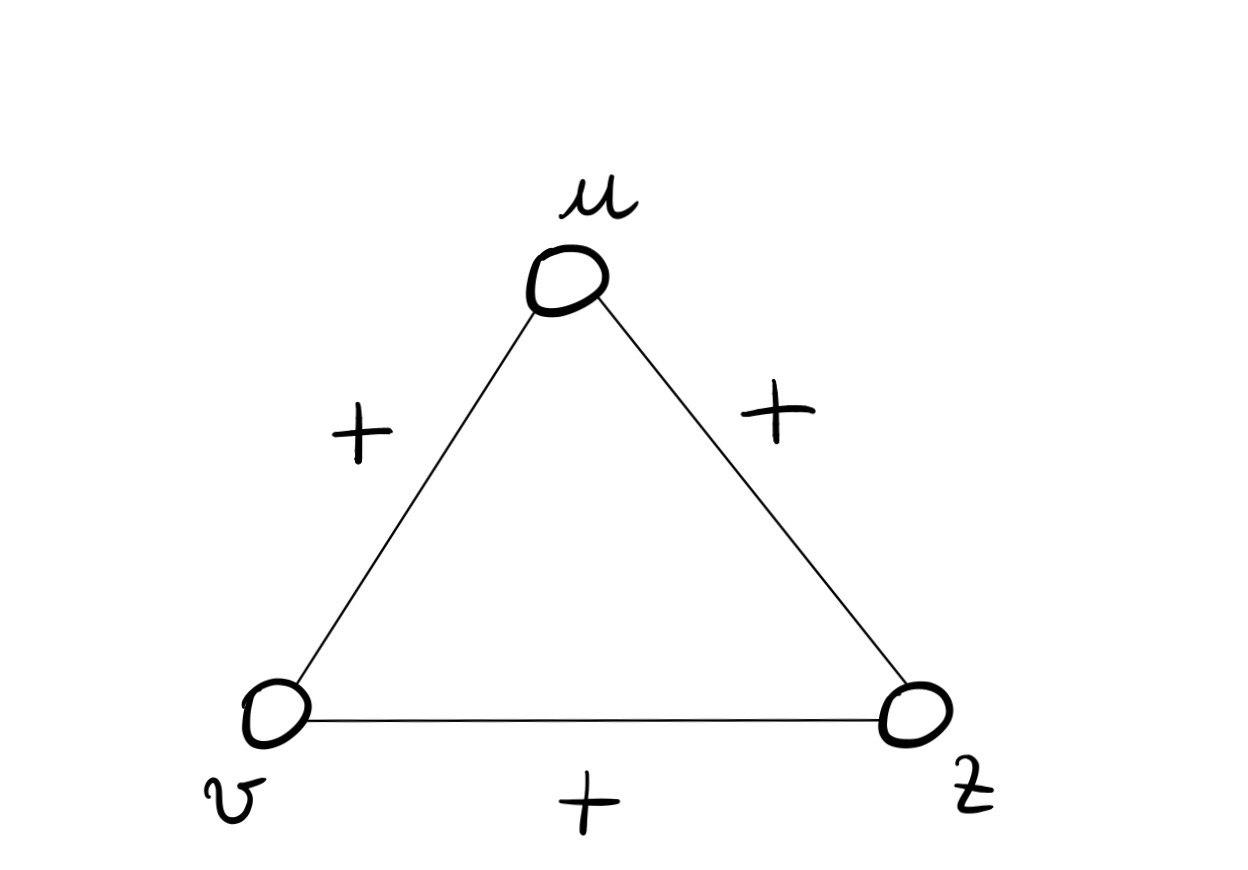
In questa struttura infatti è difficile creare delle situazioni di conflitto e instabilità.
Il triangolo in cui due amici condividono uno stesso nemico.
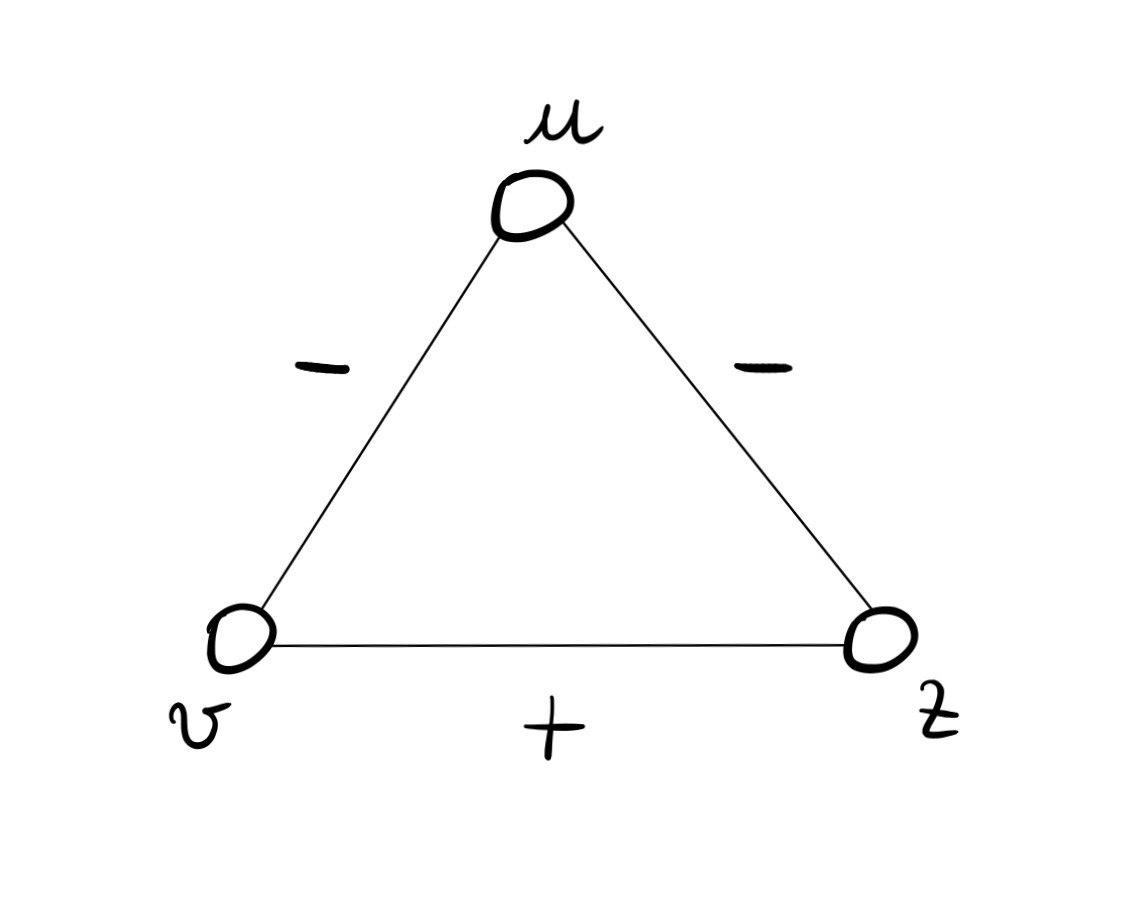
In questo caso infatti i nodi \(v\) e \(z\) possono parlare male del nodo \(u\) quando si incontrano, andando quindi ad aumentare la stabilità della rete (effetto "taglia e cuci").
Alcune configurazioni considerate strutture instabili sono,
Il triangolo in cui due amici di un nodo sono nemici tra loro.
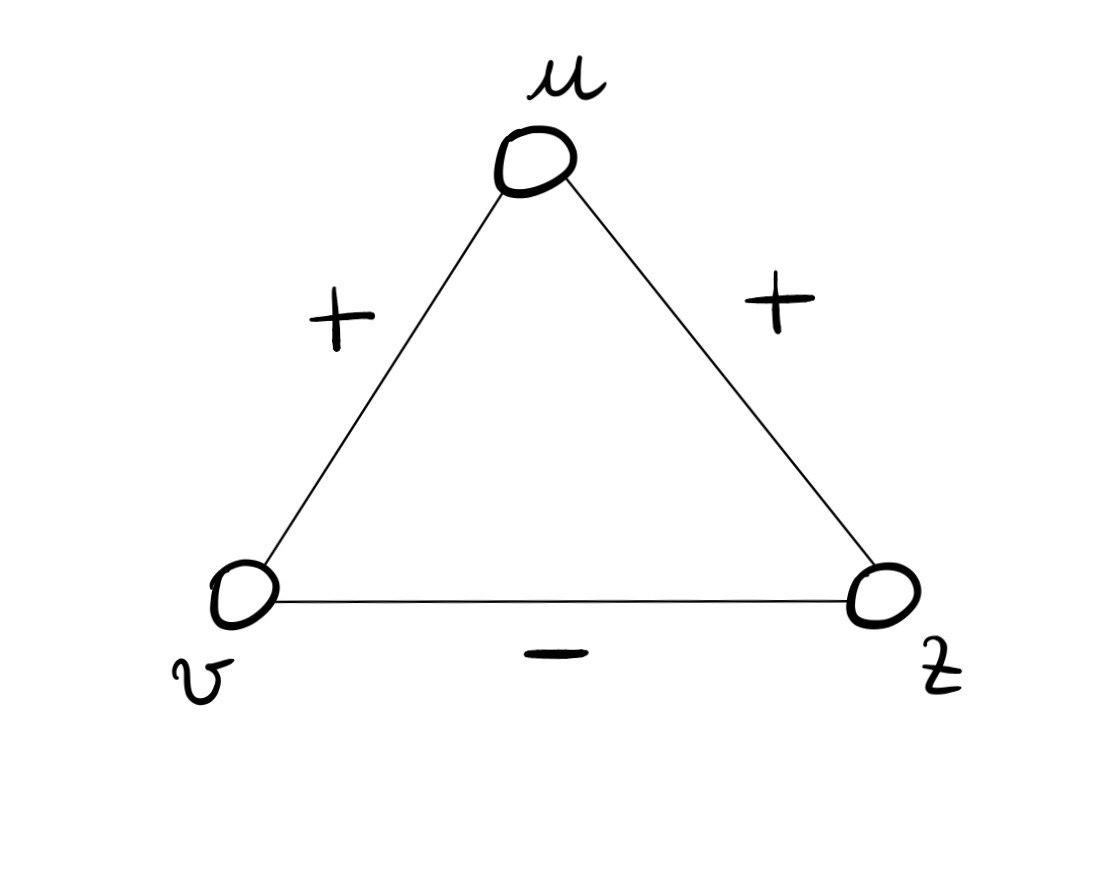
In questa situazione il nodo \(u\) sarà incentivato a risolvere i problemi tra \(v\) e \(z\).
Il triangolo in cui tutti sono nemici di tutti.
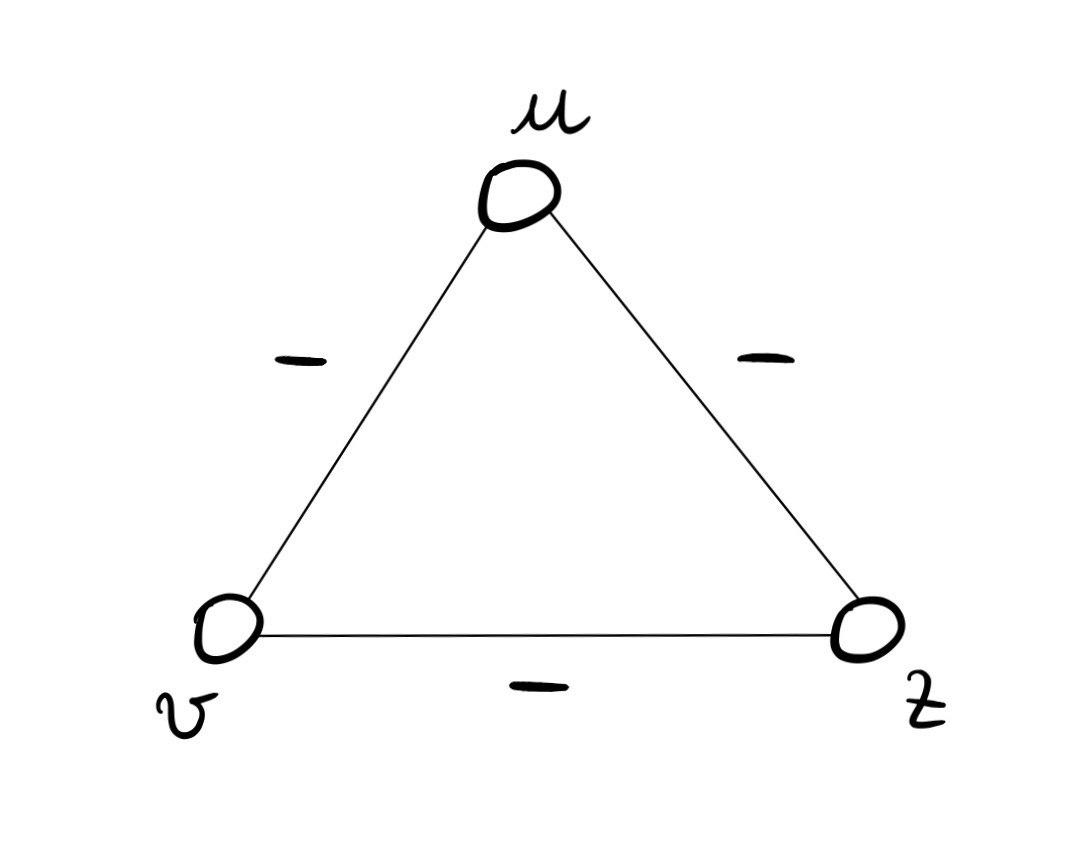
In questa situazione si potrebbero formare delle alleanze nel caso in cui ci fosse la necessità di cooperazione. Altrimenti il triangolo potrebbe rimanere stabile.
Esempio: Un esempio di instabilità di una rete sociale lo possiamo prendere dal mondo della politica, in cui è successo il seguente cambiamento nelle alleanze dei partiti politici
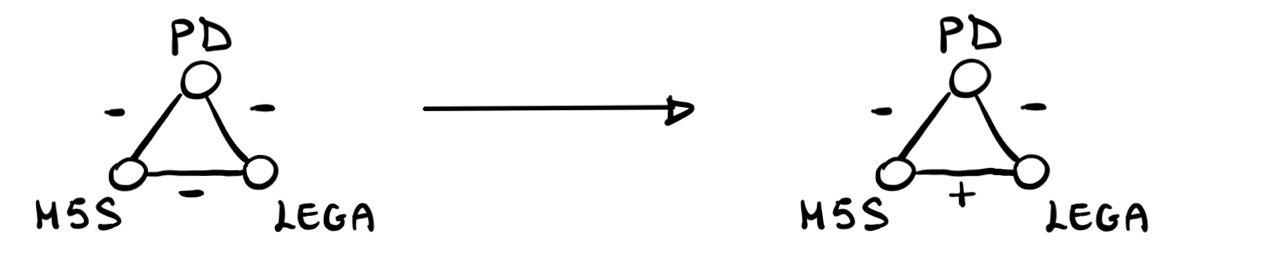
Andiamo adesso a studiare questo fenomeno della stabilità in un modo più formale. Prima ci concentreremo sulla trattazione di grafi completi, e poi alla fine rilasseremo questa ipotesi e tratteremo anche la stabilità in caso di grafi non completi.
2.2 Strutturalmente Bilanciato
Def: Un grafo \(G = (V, E^{+} \cup E^{-})\) completo è detto strutturalmente bilanciato se \(\forall u, v, z \in V:\) i tre archi del triangolo \((u, v, z)\) sono in una delle seguenti configurazioni

Volendo essere più formali, se \(\forall u, v, z \in V:\)
\[\{(u, v), (v, z), (z, u)\} \subset E^{+} \lor |\{(u,v),(v,z),(z,u)\} \cap E^{+}| = 1\]
Notiamo che non è sempre positivo il fatto che un grafo è strutturalmente bilanciato (vedi guerra fredda).
Siamo adesso interessati a trovare una caratterizzazione per i grafi strutturalmente bilanciati che sia facile da calcolare. Così facendo dato un grafo \(G\) possiamo subito vedere se è strutturalmente bilanciato. A tale fine notiamo che la proprietà di essere strutturalmente bilanciato, per come l'abbiamo definita, è una proprietà locale del grafo. Esiste anche un modo di caratterizzare il fatto che il grafo è strutturalmente bilanciato utilizzando una proprietà globale del grafo. Il seguente teorema mostra questa connessione.
Teorema:
\[\underbrace{G \text{ completo è strutturalmente bilanciato }}_{\text{Proprietà Locale}} \iff \underbrace{\exists X, Y \subseteq V: \begin{cases} X \cap Y = \emptyset, \,\,\, X \cup Y = V \\ \{(u, v): u \in X \land v \in X\} \cup \{(u, v): u \in Y \land v \in Y\} = E^{+} \\ \{(u, v): u \in X \land v \in Y\} = E^{-} \\ \end{cases}}_{\text{Proprietà Globale}}\]
Dimostrazione:
\((\Leftarrow)\) Supponiamo che \((X, Y)\) sia una partizione di \(V\) che rispetta le richieste presenti nell'enunciato. Graficamente quindi troviamo la seguente situazione
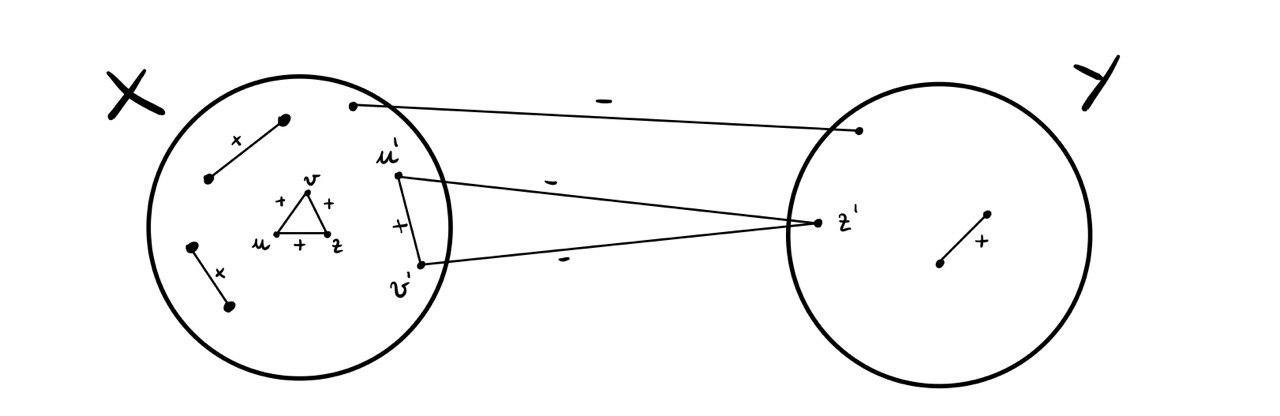
Notiamo che se \((u, v, z)\) è un triangolo in \(G\), allora abbiamo due casi:
Tutti e tre i nodi si trovano nella stessa partizione, e quindi il triangolo è bilanciato, essendo formato solamente da archi in \(E^{+}\).
Due nodi, \(u'\) e \(v'\), si trovano in una partizione, mentre il terzo nodo, \(z'\), si trova nell'altra partizione. Dato che ho esattamente un solo arco in \(E^{+}\), quello che collega i nodi nella stessa partizione, il triangolo è nuovamente bilanciato.
Dunque tutti i triangoli del grafo sono bilanciati, e quindi il grafo è strutturalmente bilanciato.
\((\Rightarrow)\) Sia \(G\) strutturalmente bilanciato. Costuriamo una partizione \((X, Y)\) di \(V\) nel seguente modo
Prendiamo un nodo \(u\) del grafo e lo mettiamo in \(X\).
Mettiamo in \(X\) tutti gli amici di \(u\).
Mettiamo in \(Y\) tutti i nodi restanti.
Andiamo adesso a far vedere che \((X, Y)\) è proprio la partizione che vogliamo
Per costruzione abbiamo che
\[X \cap Y = \emptyset, \,\,\, X \cup Y = V\]
ovvero \((X, Y)\) forma una partizione di \(V\).
Sia \((v, z): v \in X \land z \in X\). Per costruzione abbiamo che \((u, v) \in E^{+}\) e \((u, z) \in E^{+}\). Dalla completezza e stabilità di \(G\) segue che \((v, z) \in E^{+}\).
Se invece \((v, z): v \in Y \land z \in Y\), allora per costruzione abbiamo che \((u, v) \in E^{-}\) e \((u, z) \in E^{-}\). Nuovamente, dalla completezza e stabilità di \(G\) segue che \((v, z) \in E^{+}\). Dunque \(E^{+}\) è formato da coppie di nodi che appartengono allo stesso insieme.
Infine, se \((v, z): v \in X \land z \in Y\), allora per costruzione segue che \((u, v) \in E^{+}\) e \((u, z) \in E^{-}\). Dalla completezza e stabilità di \(G\) segue che \((v, z) \in E^{-}\). Dunque \(E^{-}\) è formato da coppie di nodi che appartengono ad insiemi diversi.
\[\tag*{$\blacksquare$}\]
Andiamo adesso a valutare le differenze in termini di complessità computazionale nella verifica delle due proprietà
Proprietà Locale: Per verificare la proprietà locale devo controllare tutti i triangoli del grafo, impiegando quindi
\[{{|V|}\choose{3}} \approx |V|^3 \text{ operazioni}\]
Proprietà Globale: Per verificare la proprietà globale come prima cosa si costruisce la partizione \((X, Y)\) come descritto nella dimostrazione del teorema. In particolare si costruisce un array in cui si memorizza, per ogni nodo, l'insieme, \(X\) o \(Y\), a cui il nodo appartiene. Dopo aver costruito l'array per ogni arco del grafo verifico le seguenti cose:
Se l'arco è positivo \((+)\), verifico che entrambi gli estremi sono nello stesso insieme.
Se l'arco è negativo \((-)\), verifico che entrambi gli estremi sono in insiemi diversi.
In totale questo procedimento mi costa \(O(|V| + |E|)\) operazioni.
Come è possibile notare, per grafi completi la proprietà globale è molto più facile da verificare rispetto a quella locale.
2.3 Quasi Strutturalmente Bilanciato
Def: Un grafo \(G = (V, E^{+} \cup E^{-})\) è detto quasi strutturalmente bilanciato se \(\forall u, v, z \in V\), il triangolo \((u, v, z)\) si trova nelle seguenti possibili configurazioni
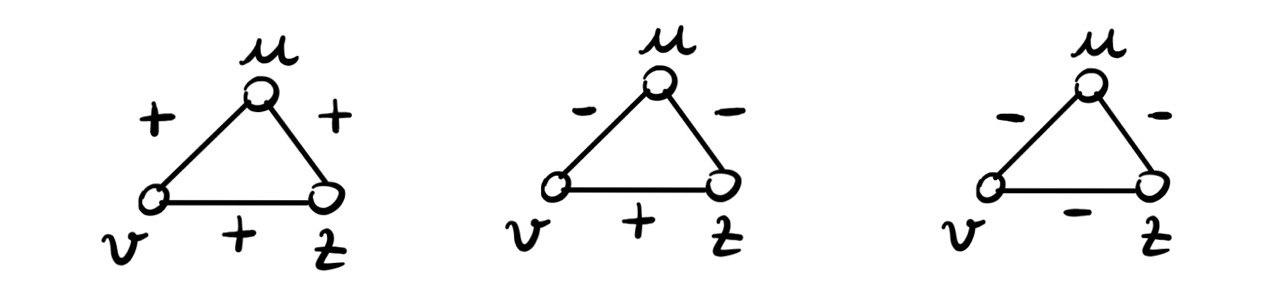
Nuovamente possiamo esprimere la proprietà di essere quasi strutturalmente bilanciato in due modi: in modo locale, come quella riportata nella definizione, e in modo globale, come mostra il seguente teorema.
Teorema:
\[\underbrace{G \text{ completo è quasi strutturalmente bilanciato }}_{\text{Proprietà Locale}} \iff \underbrace{\exists X_1, X_2, ..., X_h \subseteq V: \begin{cases} X_1, X_2, ..., X_h \text{ formano una partizione di } V \\ \forall i = 1,...,h: \forall u, v \in X_i: [(u, v) \in E^{+}] \\ \forall i \neq j: \forall u \in X_i: \forall v \in X_j: [(u, v) \in E^{-}] \end{cases}}_{\text{Proprietà Globale}}\]
Dimostrazione:
\((\Leftarrow)\) Sia \(X_1, X_2, ..., X_h\) la partizione richiesta. Graficamente troviamo una figura analoga alla seguente
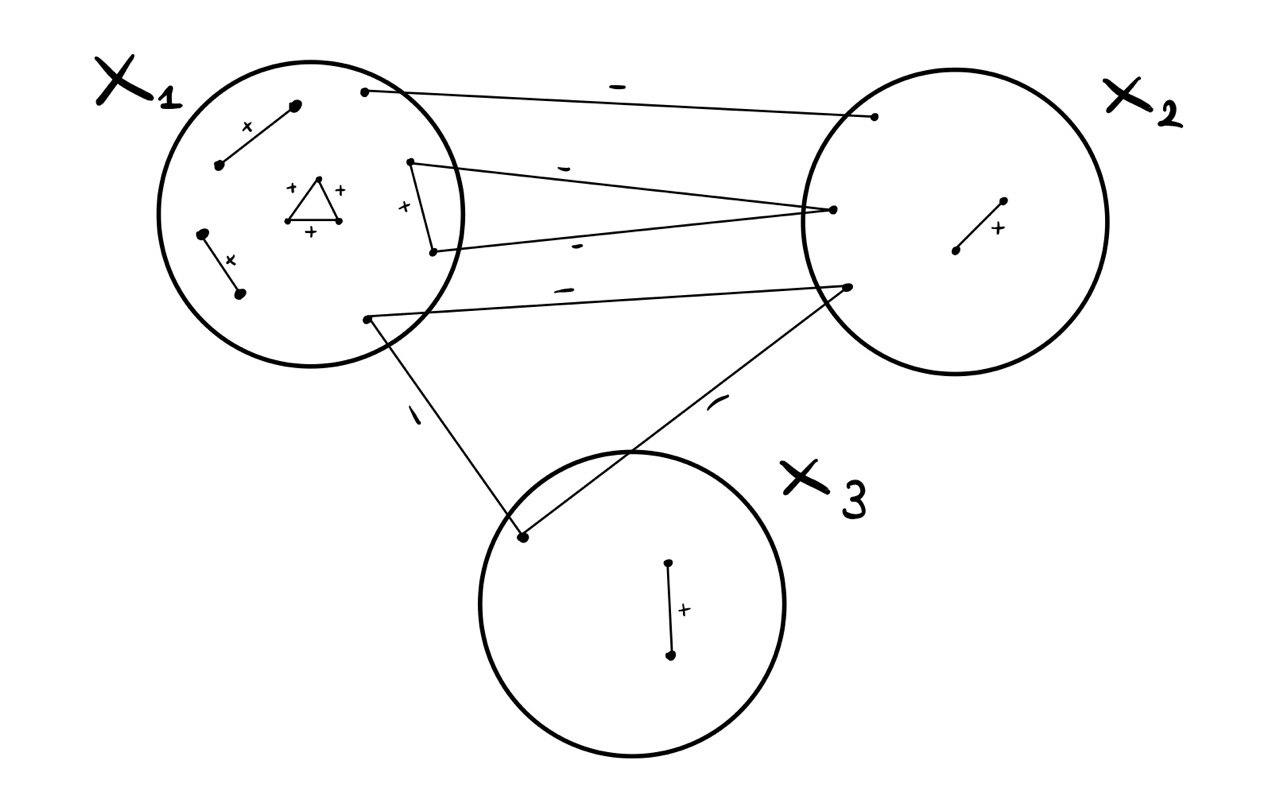
Notiamo che in qualunque modo scegliamo un triangolo, troviamo sempre una delle seguenti configurazioni

dunque il relativo grafo è quasi strutturalmente bilanciato.
\((\Rightarrow)\) Sia \(G\) completo e quasi strutturalmente bilanciato. Costruiamo la partizione \((X_1, X_2, ..., X_h)\) di \(V\) nel seguente modo:
Prendo un nodo \(u \in V\) e metto in \(X_1\) \(u\) e tutti i suoi amici.
Se rimangono altri nodi, ne prendo uno e lo metto in \(X_2\) assieme ai suoi amici.
In generale ripeto questo procedimento fino a quando non ho terminato tutti i nodi.
Dimostriamo adesso che la partizione \((X_1, X_2, ..., X_h)\) rispetta le richieste dell'enunciato
Come prima cosa dalla costruzione segue che \((X_1, X_2, ..., X_h)\) forma una partizione di \(V\).
Il resto della dimostrazione consiste nel far vedere che, dato un arco \((u, v)\), se \(u\) e \(v\) appartengono allo stesso insieme \(X_i\) della partizione allora l'arco è positivo, e se \(u\) e \(v\) appartengono a due insiemi diversi \(X_i\) e \(X_j\), allora l'arco è negativo. I dettagli non sono riportati in quanto lo schema della dimostrazione è analogo a quello visto precedentemente.
\[\tag*{$\blacksquare$}\]
3 Reti Segnate (non-complete)
Andiamo adesso a rilassare le ipotesi sulla completezza del grafo. A tale fine proponiamo le seguenti due definizioni:
Def. 1: Un grafo \(G = (V, E^{+} \cup E^{-})\) non completo è strutturalmente bilanciato se esiste un modo di completarlo in un grafo completo strutturalmente bilanciato.
Def. 2: Un grafo \(G = (V, E^{+} \cup E^{-})\) non completo è strutturalmente bilanciato se esiste una partizione \((X, Y)\) di \(V\) tale che
\(\forall (u, v) \in E: u \in X \land v \in X \implies (u, v) \in E^{+}\)
\(\forall (u, v) \in E: u \in Y \land v \in Y \implies (u, v) \in E^{+}\)
\(\forall (u, v) \in E: u \in X \land v \in Y \implies (u, v) \in E^{-}\)
Andiamo adesso a far vedere che queste due definizioni sono equivalenti.
Teorema: Def. 1 \(\iff\) Def. 2
Dimostrazione:
\((\Rightarrow)\) Sia \(G^{*} = (V, E^{*^{+}} \cup E^{*^{-}})\) il completamento bilanciato di \(G\). Dato che \(G^*\) è completo e strutturalmente bilanciato, per il teorema dimostrato in precedenza segue che esiste una partizione \((X, Y)\) di \(V\) che rispetta le richieste della Def. 2.
Notando che \(E^{+} \subseteq E^{*^{+}}\) e \(E^{-} \subseteq E^{*^{-}}\), e che la rimozione di qualche arco non compromette le proprietà di \((X, Y)\), concludiamo che \((X, Y)\) rispetta le condizioni richieste dalla Def. 2 anche per \(G\).
\((\Leftarrow)\) Sia \((X, Y)\) la partizione di \(G\). Per completare \(G\) aggiungo al grafo ogni arco mancante \((u, v)\) etichettandolo nel seguente modo:
Se \(u\) e \(v\) appartengono allo stesso insieme tra \(X\) e \(Y\), segno l'arco con \(+\).
Se \(u\) e \(v\) appartengono a due insiemi diversi tra \(X\) e \(Y\) segno l'arco con \(-\).
Dal teorema precedente segue che il grafo \(G^*\) costruito è strutturalmente bilanciato.
\[\tag*{$\blacksquare$}\]
In caso di grafi non completi, è difficile utilizzare in modo pratico sia la Def. 1 sia la Def. 2. Necessitiamo dunque di una nuova caratterizzazione, che è offerta dal seguente risultato
Teorema: Un grafo \(G = (V, E^{+} \cup E^{-})\) non completo è strutturalmente bilanciato se e solo se \(G\) non contiene cicli con un numero dispari di archi negativi.
Dimostrazione:
\((\Rightarrow)\) Dimostriamo il contrario considerando il seguente grafo
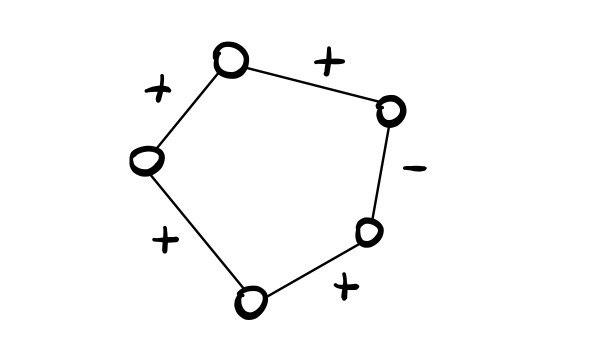
Notiamo che il grafo presenta un ciclo con un numero dispari di archi negativi. Notiamo inoltre che non siamo in grado di partizionare il grafo come richiesto dalla Def. 2. Dunque il grafo \(G\) non è strutturalmente bilanciato.
\((\Leftarrow)\) Consideriamo \(G^{+} := G - E^{-} = (V, E^+)\), e dividiamolo nelle sue componenti connesse, ottenendo così il grafo delle componenti connesse \(G^{S}_+\).
Notiamo che non esistono archi negativi tra i nodi contenuti in una componente connessa, in quanto altrimenti avrei un ciclo con un arco negativo. Da questo ne segue che gli archi negativi connettono nodi presenti in diverse componenti connesse. Viceversa, le componenti connesse sono collegate tra loro solo tramite archi negativi.
Cominciamo ad aggiungere al grafo \(G^S_+\) tutti gli archi negativi presenti in Eandando ad eseguire la corretta conversione \(\text{nodo} \to \text{componente connessa}\) per ottenere il grafo \(G^S\).
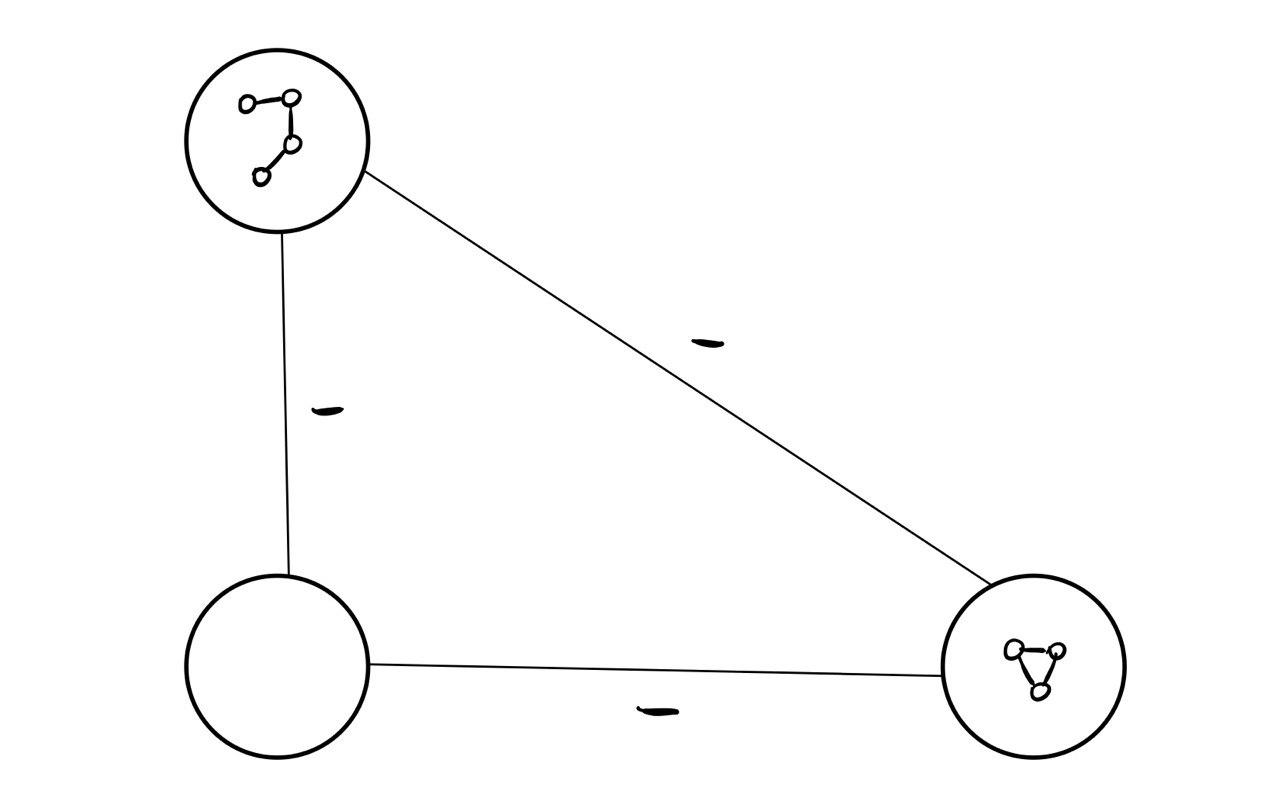
A questo punto osserviamo che se ho un ciclo con un numero dispari di archi negativi nel grafo \(G^S\), allora ho anche un ciclo con un numero dispari di archi negativi nel grafo originale. Dalle ipotesi questo non è possibile, e dunque concludiamo che \(G^S\) non contiene cicli con un numero dispari di archi negativi.
Dato che i cicli di \(G^S\) sono formati solo da archi negativi, abbiamo che \(G^S\) non ha cicli di lunghezza dispari. Ma allora \(G^S\) è 2-colorabile tramite una BFS. Posso quindi colorare \(G^S\) con i colori \(X\) e \(Y\) e trovare una partizione di \(V\) che rispetta le richieste del teorema.
\[\tag*{$\blacksquare$}\]