AR - 06 - Stabilità in Reti Segnate II
Lecture Info
Data:
Capitolo Libro: Chapter 5 - Positive and Negative Relationships
Introduzione: In questa lezione abbiamo continuato lo studio della stabilità in una rete segnata, andando a rilassare alcune ipotesi effettuate nella scorsa lezione.
1 Reti Approssimatamente Bilanciate
Continuamo lo studio della stabilità nelle reti segnate andando a rilassare la richiesta che tutti i triangoli devono essere bilanciati per avere un grafo strutturalmente bilanciato. A tale fine introduciamo la seguente defizione
Def: Sia \(G=(V, E^+ \cup E^-)\) un grafo completo. Intuitivamente diciamo che \(G\) è approssimatamente bilanciato (in senso forte) se e solo se una frazione non banale dei triangoli di \(G\) sono bilanciati.
Osservazione: Notiamo che essere bilanciati in "senso forte", significa che consideriamo il triangolo composto da tutte relazioni di inimicizia
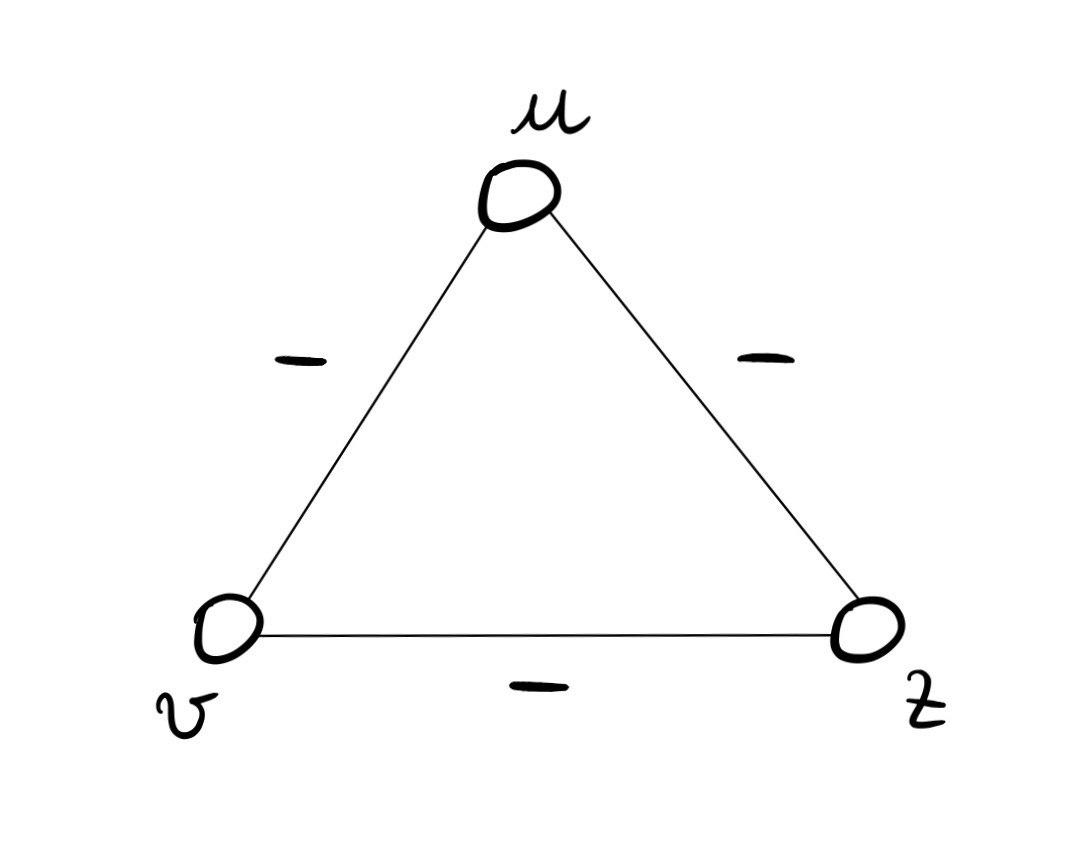
come un triangolo sbilanciato.
1.1 Caratterizzazione
Per la definizione appena data, che fa riferimento ad una proprietà locale, a differenza di quanto visto nella lezione precedente, non esiste una caratterizzazione globale equivalente della stessa proprietà. In particolare vale il seguente risultato
Teorema: Definite le seguenti quantità,
\(T :=\) numero di triangoli in \(G\)
\(\sigma :=\) numero di triangoli sbilanciati in \(G\)
\(a_X :=\) numero di archi che escono da \(X\)
\(a_X^+ :=\) numero di archi positivi che escono da \(X\)
\(a_{XY}^- :=\) numero di archi negativi che vanno da \(X\) ad \(Y\)
\(n = |V|\)
\(\delta = \sqrt[3]{\epsilon}\)
\(Y = V - X\)
Abbiamo che, \(\forall \,\, 0 < \epsilon < \frac{1}{8}: \forall \,\, 1 < \alpha < \frac{1}{\delta}\): se \(\sigma < \epsilon \cdot T\), allora \(\exists n_{\alpha, \delta}: \forall n > n_{\alpha, \delta}\), vale una delle seguenti
\(\exists X \subseteq V: |X| \geq (1 - \delta)n \,\, \land \,\, a^+_X \geq (1 - \alpha \delta)a_x\)
\(\exists X \subseteq V: |X| < (1 - \delta)n \,\, \land \,\, |V - X| < (1 - \delta)n\) and,
\(a^+_X > (1 - \alpha \delta)a_X\)
\(a^+_{V-X} > (1 - \alpha \delta)a_{V-X}\)
\(a^-_{XY} > (1 - \delta)^2 a_{XY}\)
L'enunciato del teorema ci dice che se \(\sigma < \epsilon T\), ovvero se il numero di triangoli sbilanciati nel nostro grafo \(G\) è una frazione \(\epsilon\) di \(T\), con \(0 \leq \epsilon < 1/8\), allora possono succede due cose:
Esiste un sottoinsieme di \(V\) abbastanza grande (l'insieme \(X\)) tale che gli archi positivi in questo sottoinsieme sono una buona parte degli archi totali che collegano nodi del sottoinsieme.
Esiste una partizione \(V\) in \((X, Y)\) tale che:
Le dimensioni di \(X\) e \(Y\) sono limitate dallo stesso fattore \((1 - \delta)\).
All'interno di \(X\) e \(Y\) la maggior parte degli archi sono positivi.
La maggior parte degli archi tra \(X\) e \(Y\) sono negativi.
Andiamo adesso a dimostrare tale risultato.
1.2 Dimostrazione
1.2.1 Parte 1: Trovare Nodo \(u_0\)
Cominciamo la dimostrazione andando a scegliere un nodo \(u_0 \in V\) tale che "non troppi" triangoli sbilanciati incidono su \(u_0\). A tale fine definiamo le seguenti quantità
\(\forall v \in V: \,\, w(v) := \text{ numero di triangoli sbilanciati su } v\)
\(W(G) := \sum_{v \in V} {w(v)}\)
Utilizzando la quantità \(\sigma\) definita prima abbiamo che \(W(G) = 3\sigma\), in quanto ciascun triangolo sbilanciato viene contato tre volte.
Dalle ipotesi del teorema, che ci dicono che \(\sigma < \epsilon T\), segue che
\[\begin{split} W(G) &= 3 \sigma < 3 \epsilon T \\ &= 3 \epsilon \frac{n(n-1)(n-2)}{6} \\ &= \frac{\epsilon \cdot n(n-1)(n-2)}{2} \end{split}\]
Utilizzando un ragionamento di media, notiamo che necessariamente deve esistere un \(u_0 \in V\) tale che
\[w(u_0) \leq \frac{1}{n} \cdot W(G)\]
Infatti, se così non fosse, allora la somma dei \(w(u_0)\) darebbe un risultato più grande di \(W(G)\), il che non può essere. Ma allora troviamo che
\[\begin{split} w(u_0) &\leq \frac{1}{n} W(G) \\ &< \frac{1}{n} \cdot \frac{\epsilon n(n-1)(n-2)}{2} \\ &= \frac{\epsilon (n-1) (n-2)}{2} \\ &< \frac{\epsilon n^2}{2} \end{split}\]
Possiamo quindi concludere che
\[\exists u_0 \in V: \,\, w(u_0) < \frac{\epsilon n^2}{2}\]
tale \(u_0\) sarà utilizzato per la costruzione della partizione \((X, Y)\).
1.2.2 Parte 2: Costruzione partizione (X, Y)
La partizione \((X, Y)\) di \(V\) viene costruita utilizzando il nodo \(u_0\) trovato nella sezione precedente nel seguente modo:
\(X := \{u_0\} \cup \{v \in V: \,\, (u_0, v) \in E^+\}\)
\(Y := V - X\)
L'idea è quindi che \(X\) contiene \(u_0\) e tutti gli amici di \(u_0\), mentre \(Y\) contiene i restanti nodi, ovvero i nemici di \(u_0\).
1.2.3 Parte 3: Calcolo di \(a^-_X, a_Y^-, a_{XY}^+\)
Andiamo adesso a calcolare delle quantità importanti che veranno poi utilizzate nella parte finale della dimostrazione.
Calcolo di \(a^-_X := \text{ numero archi negativi in } X\)
Ad ogni arco negativo \(e^- = (u, v)\), con \(u, v \in X\), corrisponde un triangolo sbilanciato e incidente ad \(u_0\). Graficamente infatti abbiamo la seguente situazione
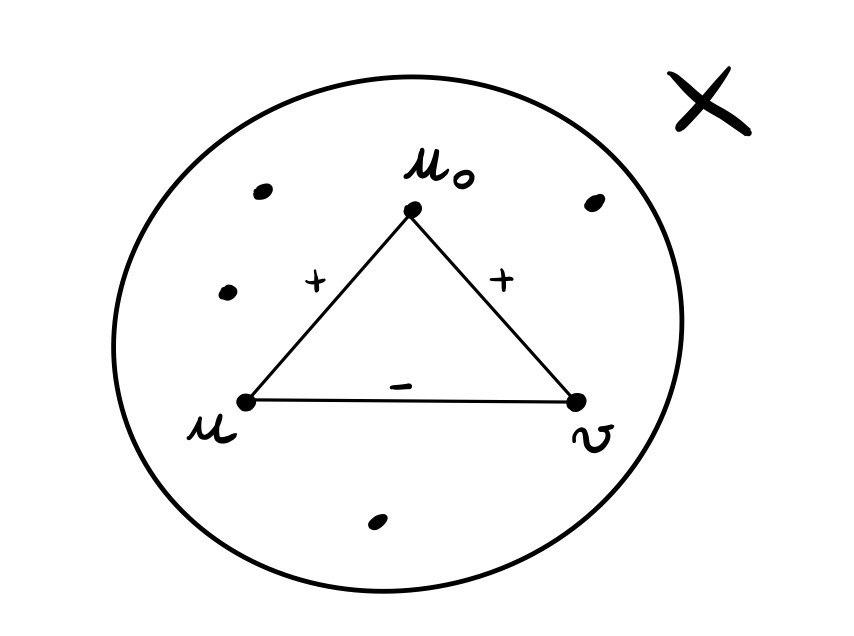
Ma allora vale il seguente upper bound,
\[a^-_X \leq w(u_0) \leq \epsilon \frac{n^2}{2}\]
Osservazione: Notiamo che vale solamente un upper bound in quanto possono esistere dei triangoli sbilanciati incidenti a \(u_0\) che però non sono associati ad archi negativi in \(X\).
Calcolo di \(a^-_Y := \text{ numero archi negativi in } Y\)
Ad ogni arco negativo \(e^- = (u, v)\) con \(u, v\) in \(Y\), corrisponde un triangolo sbilanciato e incidente ad \(u_0\). Graficamente infatti abbiamo la seguente situazione
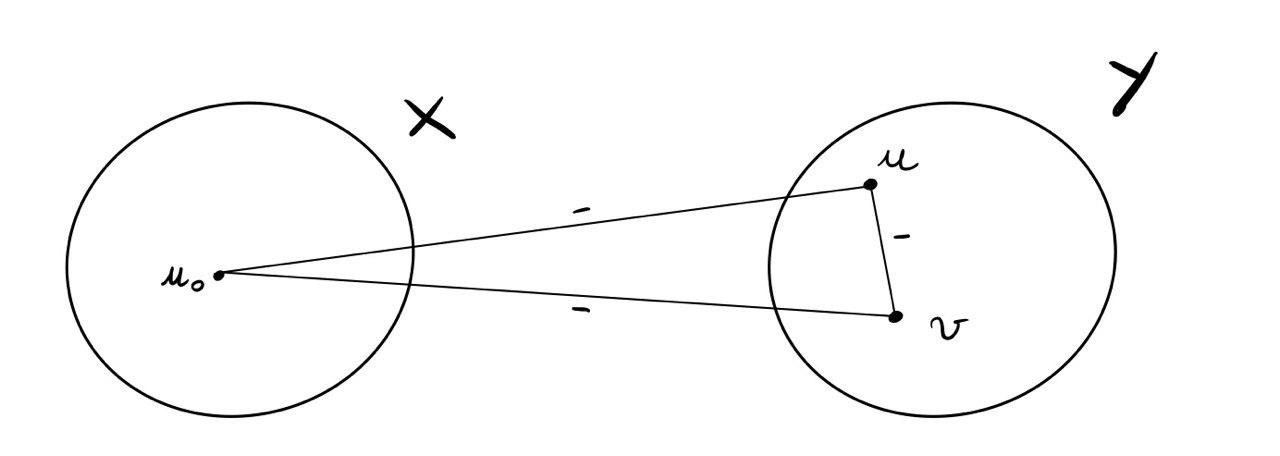
Troviamo quindi nuovamente il seguente upper bound,
\[a^-_Y \leq w(u_0) \leq \epsilon \frac{n^2}{2}\]
Calcolo di \(a^+_{XY} := \text{ numero archi positiv tra } X \text{ e } Y\)
Ad ogni arco positivo \(e^+ = (u, v)\) con \(u \in X\) e \(v \in Y\), corrisponde un triangolo sbilanciato e incidente ad \(u_0\). Graficamente infatti abbiamo la seguente situazione
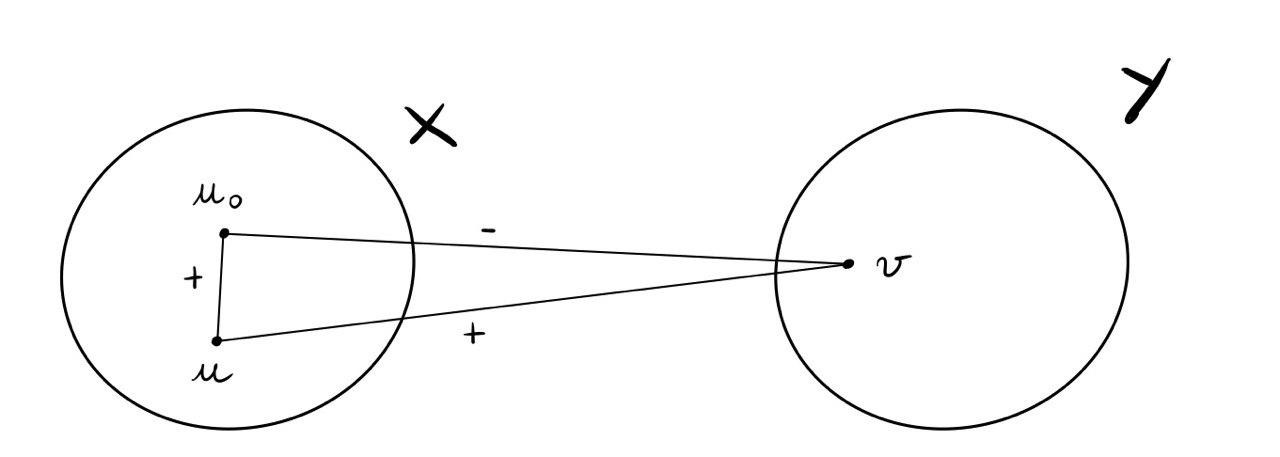
Ma allora,
\[a^+_{XY} \leq w(u_0) \leq \epsilon \frac{n^2}{2}\]
1.2.4 Parte 4: Dimostrazione casi
Utilizzando i valori \(a^-_X, a_Y^-, a_{XY}^+\) calcolati nella sezione precedente, siamo adesso in grado di dimostrare i vari casi.
Caso \(|X| \geq (1 - \delta)n\)
In questo caso, dato che \(\delta = \sqrt[3]{\epsilon} < \sqrt[3]{1/8} = 1/2\), abbiamo che l'insieme \(X\) contiene più della meta dei nodi.
Notiamo inoltre che
\[a_x = \frac{|X|(|X| - 1)}{2} > \frac{1}{2} \cdot |X| \cdot (|X|-1) > \frac{1}{2} \cdot \frac{n}{2} \cdot \frac{n-2}{2} = \frac{n(n-2)}{8}\]
Procediamo quindi riscrivendo \(a^-_X\) nel seguente modo
\[\begin{split} a^-_X &= a^-_X \cdot \frac{a_X}{a_X} \\ &< \frac{\epsilon n^2}{2} \cdot \frac{1}{a_X} \cdot a_X \\ &< \frac{\epsilon n^2}{2} \cdot \frac{8}{n(n-2)} \cdot a_X \\ &= 4 \epsilon \cdot \frac{n}{n-2} \cdot a_X \\ &= 4 \delta^3 \cdot \frac{n}{n-2} \cdot a_X \\ &< \delta \cdot \frac{n}{n-2} \cdot a_X \\ \end{split}\]
Per trovare il valore di \(n\) tale che \(\delta \cdot \frac{n}{n-2} \cdot a_X < \delta \cdot \alpha \cdot a_X\), impostiamo la seguente disuguaglianza
\[\begin{split} \frac{n}{n-2} < \alpha &\iff n < n \cdot \alpha - 2 \alpha \\ &\iff n(\alpha - 1) > 2\alpha \\ &\iff n > \frac{2 \alpha}{\alpha - 1} \end{split}\]
Dunque, definendo \(n_{\alpha, \delta} := \frac{2 \alpha}{\alpha -1}\), troviamo che \(\forall n > n_{\alpha, \delta}:\)
\[a_X^+ = a_X - a_X^- > a_X - \delta \cdot \alpha \cdot a_X > (1 - \delta \alpha) a_X\]
che era proprio ciò che volevamo dimostrare.
Caso \(|X| < (1 - \delta)n\)
In questo caso notiamo che
\[|V| = | V - X | > n - (1 - \delta)n = \delta n\]
Dunque, se \(|Y| \geq (1 - \delta)n\), allora dato che \(a_Y^- < \frac{\epsilon n^2}{2}\), possiamo ripetere lo stesso procedimento di prima per ottenere che \(a^+_Y > (1 - \alpha \delta)a_Y\), andandoci quindi a ricongiungere con il caso 1.
Supponiamo dunque che ci troviamo nella situazione in cui sia \(X\) che \(Y\) non sono molto grandi. Formalmente, tale che
\[\delta n < |X| < (1 - \delta)n \,\,\, \land \,\,\, \delta n < |Y| < (1 - \delta) n\]
Andiamo quindi a dimostrare le tre richieste presenti nell'enunciato.
Iniziamo dimostrando il terzo punto (3), che dice che \(a_{XY}^- > (1 - \delta)^2 a_{XY}\). A tale fine notiamo che
\[a_{XY} = |X| \cdot |Y| = |X| \cdot (n - |X|)\]
Definiamo quindi la funzione \(z(x) := x(n - x)\), che graficamente può essere rappresentata come segue
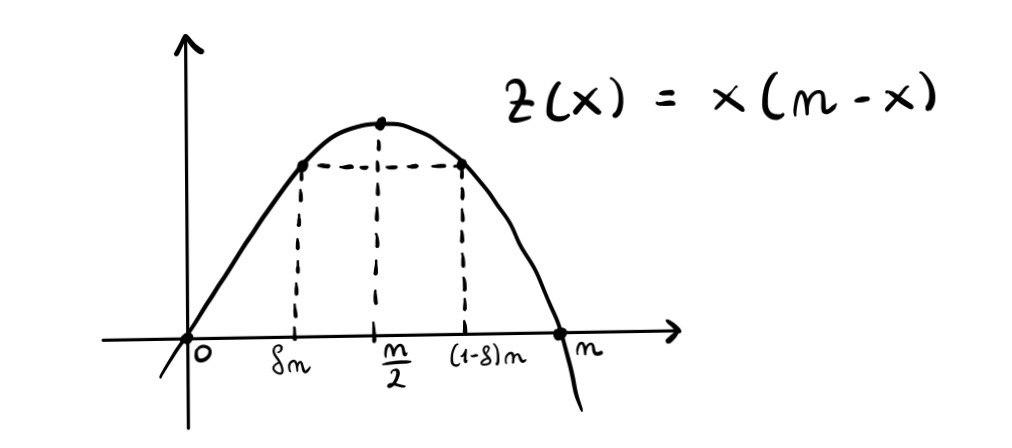
Notiamo che \(z(x)\) è una parabola con concavità verso il basso, che si annulla in \(0\) e \(n\), e con massimo in \(n/2\).
Dal fatto che \(x \in [\delta n, (1 - \delta)n]\), ne consegue che
\[\begin{split} a_{XY} > z(\delta n) &= \delta n (n - \delta n) \\ &= n^2 (\delta - \delta^2) \\ &> ^2 (\delta - \frac{\delta}{2}) \\ &= n^2 \cdot \frac{\delta}{2} \\ \end{split}\]
Utilizzando il procedimento visto prima, riscriviamo \(a_{XY}^+\) nel seguente modo
\[\begin{split} a_{XY}^+ &= a_{XY}^+ \cdot \frac{a_{XY}}{a_{XY}} \\ &< \frac{\epsilon n^2}{2} \cdot \frac{1}{a_{XY}} \cdot a_{XY} \\ &< \frac{\epsilon n^2}{2} \cdot \frac{2}{n^2 \delta} \cdot a_{XY} \\ &= \frac{\delta^3}{\delta} a_{XY} \\ &= \delta^2 a_{XY} \\ \end{split}\]
Complementando otteniamo quindi
\[a_{XY}^- = a_{XY} - a_{XY}^+ > a_{XY} - \delta^2 a_{XY} = (1 - \delta^2) a_{XY}\]
che è proprio ciò che volevamo dimostrare.
Dimostriamo adesso il caso (1), ovvero che \(a_X^+ > (1 - \alpha \delta)a_X\). Il caso (2) si dimostra in modo analogo.
A tale fine ricordiamo che \(\delta n < |X|\), e quindi che
\[ a_X = \frac{|X| \cdot (|X| - 1)}{2} > \frac{\delta n (\delta n - 1)}{2}\]
Riscrivendo \(a_X^-\) otteniamo
\[\begin{split} a_X^- &= a_X^- \cdot \frac{a_X}{a_X} \\ &= \frac{\epsilon n^2}{2} \cdot \frac{1}{a_X} \cdot a_X \\ &= \frac{\epsilon n^2}{2} \cdot \frac{2}{\delta n (\delta n -1)} \cdot a_X \\ &= \frac{\delta^3 n}{\delta(\delta n - 1)} \cdot a_X \\ &= \frac{\delta^2 n}{\delta n - 1} \cdot a_X \\ &= \delta \cdot \frac{\delta n }{\delta n - 1} \cdot a_X \end{split}\]
Per trovare il valore di \(n\) tale che \(\delta \cdot \frac{\delta n }{\delta n - 1} \cdot a_X < \delta \cdot \alpha \cdot a_X\) impostiamo la seguente disuguaglianza,
\[\begin{split} \alpha > \frac{\delta n}{\delta n - 1} &\iff \alpha \delta n - \alpha > \delta n \\ &\iff n(\alpha \delta - \delta) > \alpha \\ &\iff n > \frac{\alpha}{\alpha \delta - \delta} \\ &\iff n > \frac{\alpha}{\delta(\alpha -1)} \\ \end{split}\]
Dunque, definendo \(n_{\alpha, \delta} := \frac{\alpha}{\delta (\alpha -1)}\), troviamo che \(\forall n > n_{\alpha, \delta}\):
\[a_X^+ = a_X - a_X^- > a_X - \delta \alpha a_X = (1 - \delta \alpha) a_X\]
che è proprio quello che volevamo dimostrare.
Avendo dimostrato tutti i casi, la dimostrazione è quindi conclusa.
\[\tag*{$\blacksquare$}\]