AR - 07 - Reti di Informazioni I

Nel 1999 un gruppo di ricercatori si è messo ad analizzare parte della struttura del grafo definito dal W.W.W. La struttura scoperta ha preso il nome di Bow tie structure, e può essere raffigurata come segue

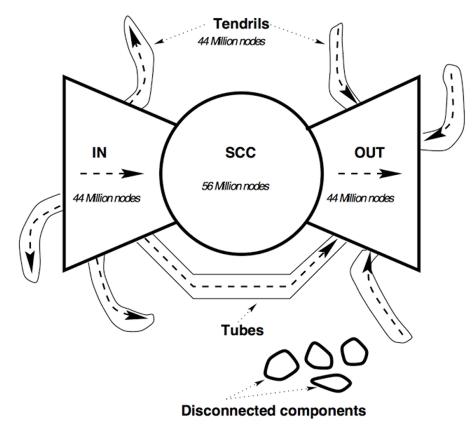
Guardando questa struttura notiamo come il grafo del Web è un grafo quasi completamente connesso, e tendenzialmente sparso, costituito da tre blocchi principali, in cui il blocco più grande è una componente fortemente connessa chiamata anche giant component e costituita approssimatamente dal \(33\%\) di tutti i nodi del Web.

Avendo visto la struttura del Web, siamo adesso interessati a definire degli algoritmi che ci possano aiutare nella ricerca delle informazioni all'interno del W.W.W.

Il problema della ricerca delle informazioni è antico quanto l'introduzione della scrittura. Esiste però una importante asimettria nella ricerca delle informazioni tra il mondo prima del Web e il mondo dopo il Web. Nel passato infatti il problema era reperire i dati, che erano molto rari e quindi preziosi. Nel presente invece data la grande mole di dati che vengono generati ogni giorno, specialmente dalle piattaforme social, il problema diventa quindi filtrare i dati, per ottenere tra tutti i dati disponibili quelli veramente utili al nostro scopo.

Al fine di filtrare le informazioni è stato quindi introdotto il concetto di ranking. Il ranking consiste nell'ordinare i documenti presenti nel web in base ad una particolare richiesta, detta anche search query. Tramite il ranking siamo in grado di capire quali sono i documenti che contengono le informazioni più rilevanti per la nostra ricerca. Nel corso in particolare vedremo due algoritmi di ranking, che sono:

• Hubs and Authorities

• Page Ranking

Osservazione: Il problema del ranking è affrontato in modo più dettagliato nel corso di Information Retrieval.

Sia \(M\) la matrice \(n \times n\) di adiacenza del grafo delle pagine definita come segue

\[M_{i, j} := \begin{cases} 1 &, \text{se } P_i \to P_j \\ 0 &, \text{altrimenti} \\ \end{cases}\]

Utilizzando la matrice \(M\) appena definita possiamo esprimere i valori di authorities e hubs nel seguente modo

\[\begin{align} a_i^k &= \sum_{j = 1}^n M_{j, i} \cdot h_j^{k-1}\\ h_i^k &= \sum_{j = 1}^n M_{i, j} \cdot a_j^k \end{align}\]

Infine, volendo utilizzate una notazione vettoriale per compattare i valori di authorities e hubs, otteniamo la seguente scrittura ricorsiva

\[\begin{align} \textbf{a}^k &:= M^T \cdot \textbf{h}^{k-1} \\ \textbf{h}^k &:= M \cdot \textbf{a}^k \end{align}\]

Espandendo il valore delle authorities \(\textbf{a}^k\) utilizzando l'ultima notazione utilizzata otteniamo la seguente espressione

\[\begin{split} \textbf{a}^k &= M^T \cdot \textbf{h}^{k-1} \\ &= (M^T \cdot M)^1 \cdot \textbf{a}^{k-1} \\ &= (M^T \cdot M)^1 \cdot M^T \cdot \textbf{h}^{k-2} \\ &= (M^T \cdot M)^1 \cdot M^T \cdot M \cdot \textbf{a}^{k-2} \\ &= (M^T \cdot M)^2 \cdot \textbf{a}^{k-2} \\ &= \ldots \\ &= (M^T \cdot M)^{k-1} \cdot \textbf{a}^1 \\ &= (M^T \cdot M)^{k-1} \cdot M^T \cdot \textbf{h}^0 \\ \end{split}\]

Per quanto riguarda il valore degli hubs \(\textbf{h}^k\) invece otteniamo la seguente espressione

\[\begin{split} \textbf{h}^k &= M \cdot \textbf{a}^{k} \\ &= (M \cdot M^T)^1 \cdot \textbf{h}^{k-1} \\ &= (M \cdot M^T)^1 \cdot M \cdot \textbf{a}^{k-1} \\ &= (M \cdot M^T)^1 \cdot M \cdot M^T \cdot \textbf{h}^{k-2} \\ &= (M \cdot M^T)^2 \cdot \textbf{h}^{k-2} \\ &= \ldots \\ &= (M \cdot M^T)^{k-1} \cdot \textbf{h}^{1} \\ &= (M \cdot M^T)^{k-1} \cdot M \cdot \textbf{a}^1 \\ &= (M \cdot M^T)^{k-1} \cdot M \cdot M^T \textbf{h}^0 \\ &= (M \cdot M^T)^k \cdot \textbf{h}^0 \\ \end{split}\]

Abbiamo quindi trovato le seguenti formule

\[\begin{align} \textbf{a}^k &= (M^T \cdot M)^{k-1} \cdot M^T \cdot \textbf{h}^0\\ \textbf{h}^k &= (M \cdot M^T)^k \cdot \textbf{h}^0\\ \end{align}\]

A questo punto notiamo che, scritto in questo modo, il vettore \(\textbf{h}^k\) non potrà mai convergere a qualcosa di significativo al crescere di \(k\). Infatti, o valore di \(M \cdot M^T\) è più piccolo di \(1\), e quindi \(\textbf{h}^k \to 0\) per \(k \to \infty\), oppure il valore di \(M \cdot M^T\) è più grande di \(1\) e quindi \(\textbf{h}^k \to \infty\) per \(k \to \infty\).

Al fine di avere una possibilità di convergenza significativa l'idea è quella di normalizzare ad ogni passo per una costante \(c\), come formalizzato dal seguente teorema.

Teorema: Esiste una costante \(c \in \mathbb{R} - \{0\}\), tale che

\[ \forall \textbf{h}^0 > 0: \,\, \exists \textbf{h}^{(*)}: \,\, \lim_{k \to \infty} \frac{\textbf{h}^k}{c^k} = \textbf{h}^{(*)}\]

Il teorema afferma che esiste un valore di normalizzazione \(c\) tale che, se partiamo da un qualunque vettore iniziale \(\textbf{h}^0\), il processo di hubs and authorities riesce a convergere al vettore \(\textbf{h}^{(*)}\). La potenza di questo teorema è che il valore \(c\) non dipende dal vettore scelto inizialmente, ma solamente dalla matrice \(M\) del grafo.

Da un punto di vista implementativo, l'introduzione di questa costante di normalizzazione \(c\) si riflette nel seguente modo rispetto al calcolo di \(\textbf{h}^{k+1}\)

\[\textbf{h}^{k+1} = \frac{M \cdot M^T}{c} \cdot \textbf{h}^k\]

Andiamo adesso a dimostrare tale risulato.

Dimostrazione: Iniziamo notando che, se l'enunciato del teorema è vero, abbiamo che al limite vale la seguente cosa

\[\begin{split} \textbf{h}^{(*)} = \frac{(M \cdot M^T)}{c} \cdot \textbf{h}^{(*)} &\implies (M \cdot M^T) \cdot \textbf{h}^{(*)} = c \cdot \textbf{h}^{(*)}\\ &\implies c \text{ è un autovettore della matrice } M \cdot M^T \end{split}\]

Continuiamo notando che \(M \cdot M^T\) è una matrice simmetrica, ovvero tale che

\[(M \cdot M^T)^T = (M^T)^T \cdot M^T = M \cdot M^T\]

un risultato noto ripreso dall'algebra lineare ci dice che se \(A\) è una matrice simmetrica \(n \times n\), i suoi autovettori formano una base ortonormale per lo spazio \(\mathbb{R}^n\), dove per base ortonormale intendiamo:

• Orto: I vettori sono ortogonali tra loro, ovvero il loro prodotto scalare vale sempre \(0\).

• Normale: il prodotto scalare di ogni vettore della base con se stesso fa sempre \(1\).

---

Siano \(z_1, z_2, ..., z_n\) gli autovettori di \(M^T \cdot M\), e siano \(c_1, c_2, ..., c_n\) i corrispettivi autovalori. Preso un \(x \in \mathbb{R}^n\) posso quindi esprimere \(x\) utilizzando la base \(z_1, z_2, ..., z_n\) nel seguente modo

\[ x = p_1 \cdot z_1 + p_2 \cdot z_2 + ... + p_n \cdot z_n\]

vale quindi il seguente risultato

\[\begin{split} (M \cdot M^T) \cdot x &= (M \cdot M^T) \cdot(p_1 \cdot z_1 + p_2 \cdot z_2 + ... + p_n \cdot z_n) \\ &= (M \cdot M^T) \cdot p_1 \cdot z_1 + (M \cdot M^T) \cdot p_2 \cdot z_2 + ... + (M \cdot M^T) \cdot p_n \cdot z_n \\ &= p_1 \cdot (M \cdot M^T) \cdot z_1 + p_2 \cdot (M \cdot M^T) \cdot z_2 + ... + p_n \cdot (M \cdot M^T) \cdot z_n \\ &= p_1 c_1 z_1 + p_2 c_2 z_2 + ... + p_n c_n z_n \\ \end{split}\]

Andiamo adesso a scrivere \(\textbf{h}^k\) utilizando \(z_1, z_2, ..., z_n\). Per procedere quindi consideriamo le coordinate del vettore \(\textbf{h}^0\) rispetto alla base ortonormale \(\{z_1, z_2, ..., z_n\}\). Utilizando la formula trovata prima per \(\textbf{h}^k\) troviamo che

\[\begin{split} \textbf{h}^k &= (M \cdot M^T)^k \cdot \textbf{h}^0 \\ &= (M \cdot M^T)^k \cdot (q_1 \cdot z_1 + q_2 \cdot z_2 + ... + q_n \cdot z_n) \\ &= (M \cdot M^T)^{k-1} \cdot (M \cdot M^T) \cdot (q_1 \cdot z_1 + q_2 \cdot z_2 + ... + q_n \cdot z_n) \\ &= (M \cdot M^T)^{k-1} \cdot (c_1 q_1 z_1 + c_2 q_2 z_2 + ... c_n q_n z_n) \\ &= (M \cdot M^T)^{k-2} \cdot (M \cdot M^T) \cdot (c_1 q_1 z_1 + c_2 q_2 z_2 + ... c_n q_n z_n) \\ &= (M \cdot M^T)^{k-2} \cdot (c_1^2 q_1 z_1 + c_2^2 q_2 z_2 + ... c_n^2 q_n z_n) \\ &= \ldots \\ &= c_1^k q_1 z_1 + c_2^k q_2 z_2 + ... c_n^k q_n z_n \\ \end{split}\]

Abbiamo quindi trovato che

\[ \textbf{h}^k = \sum_{i = 1}^n c_i^k q_i z_i \]

---

Supponiamo ora di ordinare gli autovalori in base al loro modulo \(|c_1| \geq |c_2| \geq ... \geq |c_n|\) Abbiamo quindi due possibili casi

1. Se \(|c_1| > |c_2|\), ovvero se il primo autovalore domina su tutti gli altri, troviamo che

   \[\frac{\textbf{h}^k}{c_1^k} = \sum_{i = 1}^n \frac{c_i^k}{c_1^k} q_i z_i = \sum_{i = 1}^n \Big(\frac{c_i}{c_1}\Big)^k q_i z_i\]

   in questo caso, dato che \(|c_i/c_1| < 1\) per \(i > 1\), abbiamo che

   \[\lim_{k \to \infty} \frac{\textbf{h}^k}{c_1^k} = \lim_{k \to \infty} \sum_{i = 1}^n \Big(\frac{c_i}{c_1}\Big)^k q_i z_i = q_1 z_1\]

   e quindi, indipendentemente dal vettore iniziale \(\textbf{h}^0 > 0\) con cui iniziamo, il processo converge sempre al valore \(q_1 z_1\).

2. Nel caso in cui il primo autovalore non domina su tutti gli altri, il processo convergerà ad una combinazione lineare degli autovettori della matrice \(M \cdot M^T\) che dipende dal vettore inizialmente scelto \(\textbf{h}^0\).

\[\tag*{$\blacksquare$}\]

---

Assumendo che l'autovalore della matrice \(M \cdot M^T\) che massimizza il proprio valore assoluto sia diverso da \(0\), da quanto appena visto il processo converge a \(0\) solo quando \(q_1 = 0\), dove \(q_1\) rappresenta la prima coordinata del vettore \(\textbf{h}^0\) rispetto alla base ortonormale \(\{z_1, z_2, ..., z_n\}\) di \(\mathbb{R}^n\). A questo punto ci possiamo chiedere: quando succede che \(q_1 = 0\)?

A tale fine notiamo che

\[\begin{split} \textbf{h}^0 \cdot z_1 &= (q_1 z_1 + q_2 z_2 + ... + q_n z_n) \cdot z_1 \\ &= q_1 z_1 z_1 + q_2 z_2 z_1 + ... + q_1 z_n z_1 \\ &= q_1 \end{split}\]

in quanto \(\{z_1, z_2, ..., z_n\}\) è una base ortonormale. Ma allora \(q_1 = 0\) se e solo se il vettore \(\textbf{h}^0\) è ortogonale al primo vettore della base \(z_1\). In formula,

\[q_1 = 0 \iff \textbf{h}^0 \perp z_1\]

per dimostrare che \(q_1 \neq 0\) ci basta quindi dimostrare che nessun vettore positivo \(\textbf{h}^0 > 0\) è ortogonale a \(z_1\). La dimostrazione è spezzata in tre passi:

• Primo passo

  Supponiamo per assurdo che per ogni \(x > 0\) abbiamo che \(x \perp z_1\). Indichiamo quindi con \(x = (x_1, x_2, ..., x_n)\) le coordinate di \(x\) nello spazio canonico e definiamo il seguente vettore

  \[ x_i := (x_1, x_2, ..., x_{i-1}, x_i + 1, x_{i+1}, ..., x_n)\]

  dalle ipotesi effettuate segue che sia \(x\) che \(x_i\) sono ortogonali a \(z_1\), ovvero che

  \(\begin{cases} x \cdot z_1 = 0 \\ x_i \cdot z_1 = 0 \end{cases}\)

  Se indichiamo con \(z_1 = (z_{1,1}, z_{1,2}, ..., z_{1,n})\) le coordinate di \(z_1\) nello spazio canonico, troviamo che per ogni \(i = 1,.., n\) vale la seguente

  \[\begin{split}\begin{cases} x \cdot z_1 = 0 \\ x_i \cdot z_1 = 0 \end{cases} &\iff \begin{cases} x_1 z_{1,1} + x_2 z_{1,2} + ... + x_{i-1} z_{1, i-1} + x_i z_{1, i} + x_{i+1} z_{1, i + 1} + ... + x_n z_{1, n} = 0 \\ x_1 z_{1,1} + x_2 z_{1,2} + ... + x_{i-1} z_{1, i-1} + (x_i + 1) z_{1, i} + x_{i+1} z_{1, i + 1} + ... + x_n z_{1, n} = 0 \end{cases}\\ &\iff z_{1, i} = 0\end{split}\]

  Ma allora il vettore \(z_1\) è il vettore nullo \((0, 0, 0, ..., 0)\), e quindi non può far parte di una base ortonormale. Dato che siamo caduti in contraddizione, concludiamo che le nostre ipotesi di partenza erano sbagliate, e quindi deve necessariamente esistere un vettore \(x\) con tutte le cooridnate positive che non è ortogonale al vettore \(z_1\).

• Secondo passo

  Sia \(x > 0\) un vettore non ortogonale a \(z_1\), e consideriamo le coordinate \((p_1, p_2, ..., p_n)\) di \(x\) rispetto alla base ortonormale \(\{z_1, z_2, ..., z_n\}\).

  Definendo \(x^0 := x\), e applicando il metodo Hubs and Authorities, al passo \(k+1\) abbiamo che il vettore \(x^{k+1}\) è uguale a

  \[x^{k+1} = \frac{M \cdot M^T}{c_1} \cdot x^{k}\]

  e quindi ha necessariamente tutte le componenti positive, in quanto \(M \cdot M^T\) è una matrice a valori positivi, e \(c_1\) è assunto positivo.

  Prendendo il limite poi sappiamo che il vettore considerato converge ad una combinazione lineare degli autovettori della matrice \(M \cdot M^T\). Se ad esempio l'autovettore più grande domina su tutti gli altri, allora sappiamo che

  \[\lim_{k \to \infty} \frac{M \cdot M^T}{c_1} \cdot x^{k} = p_1 z_1\]

  In generale concludiamo che il vettore a cui convergiamo è sempre a coordinate non negative, con almeno una coordinata \(> 0\), in quanto \(p_1 \neq 0\) e \(z_1\) non è il vettore nullo.

• Terzo passo

  Sia \(y\) un qualsiasi vettore con tutte le componenti strettamente positive. Vale allora la seguente cosa

  \[p_1 z_1 \cdot y > 0\]

  dunque, togliendo \(p_1\), ottengo che \(z_1 \cdot y > 0\), e quindi che \(y\) non è ortogonale a \(z_1\).

  Infine, se considero che il vettore \(y\) è il vettore \(\textbf{h}^0\) che utilizzo per far iniziare il processo di Hubs and Authorities converge è ortogonale a \(z_1\), ho che \(\textbf{h}^0\) non è ortogonale a \(z_1\), e quindi che \(q_1 \neq 0\), che è proprio quello che volevo dimostrare.

La matrice \(M\) che abbiamo utilizzato è tale che \(M_{i,j} = 1 \iff P_i \to P_j\), ovvero \(M_{i, j} = 1\) se e solo se la pagina \(i\) punta alla pagina \(j\), e quindi una pagina non ha mai riferimenti a se stessa, ovvero \(M_{i, i} = 0, \forall i = 1, ..., n\).

Il metodo Hubs and Authorities però non utilizza la matrice \(M\), ma utilizza la matrice \(M \cdot M^T\), che è una matrice simmetrica, e quindi valgono le seguenti proprietà

• Gli autovettori formano una base ortonormale

• Gli autovalori sono tutti reali

Notiamo poi che \(M \cdot M^T\) è una matrice semi-definita positiva, ovvero tale che

\[\forall x \neq 0 \,\, : \,\, x^T A x \geq 0\]

da questo segue che i suoi autovalori non possono essere negativi.

---

Per risolvere i problemi tecnicni e avere che gli autovalori siano sempre \(> 0\), impostiamo i valori della diagonale ad \(1\), ovvero imponiamo che

\[M_{i, i} = 1, \,\,\ \forall i = 1,...,n\]

così facendo ho tutti gli autovalori \(>0\) e la matrice è definita positiva.

NOTA BENE: Dal punto di vista tecnico/matematico, questa scelta di mettere i valori della diagonale ad \(1\) è stata fatta per avere una condizione sufficiente (ma forse non necessaria), ad avere che tutti gli autovalori della matrice \(M \cdot M^T\) siano positivi.

Dal punto di vista di reti invece, questa scelta equivale a dire che ogni pagina dice di se stessa che è una pagina di autorità, che tutto sommato è una cosa intuitiva.