AR - 09 - Cascate Informative I

Consideriamo un filtro per eliminare lo spam delle e-mail che lavora sui seguenti dati:

• \(40 \%\) e-mail sono spam.

• \(1 \%\) delle e-mail di spam contengono la parola verifica

• \(0.4 \%\) delle e-mail non-spam contengono la parola verifica

Definiamo quindi i seguenti eventi

• \(M :=\) la mail ricevuta è non-spam

• \(S :=\) la mail ricevuta è spam

• \(V :=\) la mail ricevuta contiene la parola verifica

Applicando Bayes troviamo

\[\begin{split} P(S|V) &= \frac{P(V | S) \cdot P(S)}{P(V)} \\ &= \frac{P(V | S) \cdot P(S)}{P(V | S) \cdot P(S) + P(V | M) \cdot P(M)} \\ &= \frac{\frac{1}{100} \cdot \frac{4}{10}}{\frac{4}{100} \cdot \frac{4}{10} + \frac{4}{1000} \cdot \frac{6}{10}} = \frac{40}{64} = \frac{5}{8} > \frac{1}{2} \\ \end{split}\]

Dunque, se si riceve una e-mail che contiene la parola "verifica", la probabilità che l'e-mail ricevuta sia di spam è maggiore del \(50\%\).

Consideriamo due urne, \(S_1\) e \(S_2\). La prima urna, \(S_1\), ha due palline blue e una pallina rossa, mentre la seconda urna, \(S_2\), ha due palline rosse e una pallina blu. Graficamente,

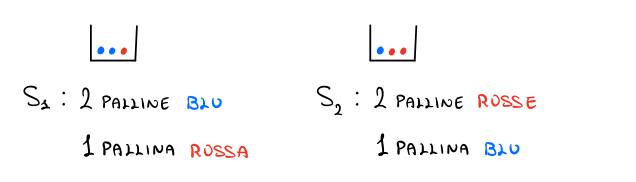
L'esperimento è quindi descritto: inizialmente viene scelta in modo casuale e uniforme una tra le due scatole. Non si sa quindi quale delle due scatole è stata scelta. Subito dopo questa scelta, \(n\) individui, in sequenza, pescano dalla scatola una pallina, la rimettono apposto, e in base al colore pescato decidono qual'è la scatola scelta inizialmente. La scelta finale di ogni individuo viene poi comunicata a tutti gli altri, mentre il colore della pallina pescata è una informazione privata di ogni singolo individuo.

Al fine di analizzare in modo matematico questo esperimento, definiamo i seguenti eventi:

• \(B :=\) L'urna scelta è \(S_1\), ovvero quella che contiene due palline blu

• \(R :=\) L'urna scelta è \(S_2\), ovvero quella che contiene due palline rosse

• \(b_i :=\) L' \(i-\) esima pallina pescata è di colore blu

• \(r_i :=\) L' \(i-\) esima pallina pescata è di colore rosso

Procediamo quindi con un po' di conti.

---

Per quanto riguarda il primo giocatore, ho che se lui pesca una pallina di colore blu, allora le sue probabilità rispetto all'urna scelta si aggiornano nel seguente modo

\[\begin{split} P(B | b_1) &= \frac{P(b_1 | B) \cdot P(B)}{P(b_1)} \\ &= \frac{P(b_1 | B) \cdot P(B)}{P(b_1 | B) \cdot P(B) + P(b_1 | R) \cdot P(R)} \\ &= \frac{\frac{2}{3} \cdot \frac12}{ \frac23 \cdot \frac12 + \frac13 \cdot \frac12} = \frac23 > \frac12\\ \end{split}\]

dunque, se il primo pesca \(blu\), allora dato che \(P(B | b) > 1/2\), per lui è più probabile che sia stata scelta l'urna \(S_1\), e dunque comunica agli altri che è stata scelta proprio \(S_1\).

---

Continuamo quindi con il secondo giocatore, nell'ipotesi che il primo abbia detto \(S_1\).

Se anche il secondo giocatore trova una pallina di colore blu, allora

\[\begin{split} P(B | b_1, b_2) &= \frac{P(b_1, b_2| B) \cdot P(B)}{P(b_1, b_2)} \\ &= \frac{P(b_1, b_2 | B) \cdot P(B)}{P(b_1, b_2 | B) \cdot P(B) + P(b_1, b_2 | R) \cdot P(R)} \\ &= \frac{\frac49 \cdot \frac12}{\frac49 \cdot \frac12 + \frac19 \frac12} = \frac45 > \frac23 \\ \end{split}\]

Se invece il secondo giocatore pesca una pallina rossa, allora

\[\begin{split} P(B | b_1, r_2) &= \frac{P(b_1, r_2| B) \cdot P(B)}{P(b_1, r_2)} \\ &= \frac{P(b_1, r_2 | B) \cdot P(B)}{P(b_1, r_2 | B) \cdot P(B) + P(b_1, r_2 | R) \cdot P(R)} \\ &= \frac{\frac29 \cdot \frac12}{\frac29 \cdot \frac12 + \frac29 \frac12} = \frac12 \\ \end{split}\]

Dunque, se il secondo giocatore pesca una pallina blu, allora dirà agli altri che l'urna pescata è \(S_1\). Se invece pesca rossa allora non ha informazioni aggiuntive, e quindi possiamo assumere dirà agli altri che l'urna pescata è \(S_2\).

---

Passiamo adesso al terzo giocatore, nell'ipotesi in cui i primi due individui hanno scelto \(S_1\)

Se il terzo giocatore pesca una pallina rossa, allora

\[\begin{split} P(B | b_1, b_2, r_3) &= \frac{P(b_1, b_2, r_3| B) \cdot P(B)}{P(b_1, b_2, r_3)} \\ &= \frac{P(b_1, b_2, r_3 | B) \cdot P(B)}{P(b_1, b_2, r_3 | B) \cdot P(B) + P(b_1, b_2, r_3 | R) \cdot P(R)} \\ &= \frac{\frac{4}{27} \cdot \frac12}{\frac{4}{27} \cdot \frac12 + \frac{2}{27} \frac12} \\ &= \frac{4}{27} \cdot \frac{27}{6} = \frac23 \\ \end{split}\]

Da questo segue che, anche se il terzo individuo pesca una pallina di colore rosso, per lui sarà comunque più probabile l'urna \(S_1\), che è quindi quella che comunicherà agli altri individui. Da questo momento in poi quindi, per ogni individuo, le uniche informazioni attendibili sulle estrazioni sono solamente le prime due estrazioni e l'estrazione effettuata dall'individuo stesso.

Quando due individui pescano in sequenza due colori uguali, diciamo che inizia una cascata informativa, in quanto tutti i restanti individui, se vogliono massimizzare la probabilità di essere corretti, dovranno per forza scegliere il colore che scelgono gli altri.

---

Calcoliamo adesso la probabilità di avere una sequenza di colori alternati

\[\begin{split} P((br)^n) &= P((br)^n |B) \cdot P(B) + P((br)^n |R) \cdot P(R) \\ &= \Big(\frac29\Big)^n \cdot \frac12 + \Big(\frac29\Big)^n \cdot \frac12 \\ &= \Big(\frac29\Big)^n \end{split}\]

Da questo segue che al crescere di \(n\) la probabilità di avere alternanze diminuisce, in quanto

\[\lim_{n \to \infty} P((br)^n) = \lim_{n \to \infty} \Big(\frac29\Big)^n = 0\]

il che implica il seguente risultato

\[\lim_{n \to \infty} P(\text{cascata in atto al passo } n) = 1\]

---

Infine, per quanto riguarda la probabilità di effettuare la scelta sbagliata, tale probabilità è almeno data dalla probabilità dei seguenti eventi

• \(P(b_1, b_2 | R) = \frac19\)

• \(P(r_1, r_2 | B) = \frac19\)

Dunque la probabilità di errore è \(\geq \frac29\).

Andiamo adesso a formalizzare una generalizzazione dell'esperimento appena analizzato. Il modello che introduciamo ha due componenti principali, che sono:

• Ci sono due stati, \(G\) e \(B\), tali che, fissato \(p \in (0, 1)\) si ha

  • \(P(G) = p\)

  • \(P(B) = 1 - p\)

• Ci sono due segnali, \(g\) e \(b\), ciascuno dei quali supporta un particolare stato (\(g\) supporta \(G\) e \(b\) supporta \(B\), e tali che, fissato \(q \in (\frac12, 1)\), si ha

  • \(P(g | G) = q \,\,\, , \,\,\, p(b | G) = 1 - q\)

  • \(P(b | B) = q \,\,\, , \,\,\, p(G | B) = 1 - q\)

Infine, si assume l'esistenza di un meccanismo di reward per gli individui che scelgono correttamente lo stato, e un meccanismo di penalizzazione se si sbaglia. Questo meccanismo viene introdotto solamente per far in modo che gli individui sono incentivati nel compiere la scelta che massimizza la loro probabilità di successo.

I segnali \(g\) e \(b\) sono segnali privati, ovvero che ciascun segnale è visibile solamente da un particolare individuo, e quindi che ciascun individuo vede solamente il proprio segnale. Le uniche informazioni di natura pubblica sono le decisioni prese dai vari individui rispetto allo stato del mondo.

Notiamo che la rete sociale utilizzata dal seguente modello può essere rappresentata come segue

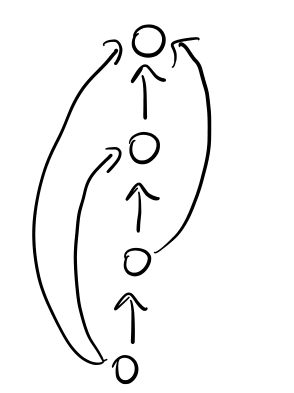
ed è una rete in cui gli archi rappresentano ciò che vedono i vari individui della rete. Nella rete è quindi presente il concetto di temporizzazione e di sequenzialità nelle varie scelte prese dagli individui.