AR - 11 - Popolarità
Lecture Info
Data:
Capitolo Libro: Chapter 18 - Power Laws and Rich-Get-Richer Phenomena
Introduzione: In questa lezione abbiamo parlato del fenomeno della popolarità nelle reti sociali e abbiamo introdotto un modello modello matematico per analizzare tali dinamiche. Tramite delle approssimazioni abbiamo visto come la popolarità dei nodi nel modello introdotto è descritta da una power law. Come ultimo argomento si è poi trattato il fenomeno della lunga coda, andandolo a collegare al concetto di power law.
1 Modelli Rich Get Richer
Abbiamo già discusso del fatto che la struttura di una rete tende a modificare se stessa indirettamente, andando a modificare il comportamento dei nodi che compongono la rete. Un esempio di questo fenomeno è visibile nelle reti sociali, in cui gli individui più popolari tendono a diventare sempre più popolari.
Per poter studiare il fenomeno della popolarità, dobbiamo studiare l'andamento del grado dei nodi in una rete. Dato che è difficile avere dati concreti su reti sociali significative realmente esistenti, l'idea è quella di definire un modello generativo che riesca a catturare qualche aspetto del concetto di popolarità. Si può quindi iniziare analizzando il modello già visto di Erdős-Rényi.
1.1 Modello Erdős-Rényi
Ricordiamo che un nel modello di Erdős-Rényi il grafo generato avevan \(n\) nodi e gli archi tra una coppia di nodi \((u, v)\) venivano generati in modo indipendente tra loro con probabilità \(p\).
Andando ad esprimere il grado di un nodo \(u \in V\) come somma di v.a.
\[X_u = \sum\limits_{\substack{ i = 1: \\i \neq u}}^n Y_{i, u} \,\,\, , \,\,\ \text{ con } Y_{i, u} = \begin{cases} 1, \,\, i \to u \\ 0, \,\, \text{ else } \end{cases}\]
avevamo trovato che il grado medio del nodo \(u\) è dato da \(\mathbb{E}[d(u)] = p \cdot (n-1)\). Infine, posto \(p = \frac{\lambda}{n}\), avevamo dimostrato che
\[P(d(u) = k) \approx \Big(\frac{\lambda e}{k}\Big)^k\]
A questo punto torna utile ricordare un importante risultato della statistica, che prende il nome di Teorema del Limite Centrale.
1.1.1 Teorema del Limite Centrale
Il Teorema del Limite Centrale ci dice che la somma di v.a. indipendenti e con la stessa distribuzione converge ad una distribuzione normale.
Dato che possiamo esprimere il grado del nodo \(u\), \(X_u\), come somma di v.a. indipendenti e aventi tutti la stessa distribuzione, abbiamo che \(X_u\) all'aumentare del numero di nodi \(n\) segue una distribuzione normale descritta dalla seguente densità
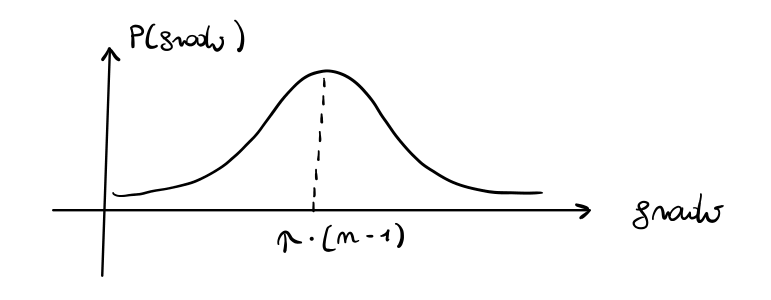
1.1.2 Secondo Chernoff Bound
Inoltre, dato che \(X_u\) è una somma di v.a. indipendenti, per calcolare la probabilità \(P(X_u > k)\), possiamo utilizzare il secondo Chernoff Bound, che dice che, dato \(\mathbb{E}[X_u] = \mu\), allora
\[P(X_u > (1 + \delta) \cdot \mu) < \bigg[ \frac{e^{\delta}}{(1 + \delta)^{1 + \delta}} \bigg]^{\mu}\]
Dunque, nel modello di Erdős-Rényi la probabilità del grado di un nodo diminuisce in modo esponenziale all'aumentare del grado. In termine di popolarità questo significa che, nel modello di Erdős-Rényi ci sono pochissimi nodi popolari.
1.2 Power Laws
A differenza di quello che ci dice il modello di Erdős-Rényi, varie ricerche hanno mostrato che nelle reti sociali e di informazioni la rete si comporta in un modo alquanto diverso: il numero di nodi popolari era molto più alto di quello che ci si sarebbe aspettati da una decrescita esponenziale, come quella presente nel modello di Erdős-Rényi. Ad esempio, nell'articolo Graph structure in the web si è scoperto che la frazione delle pagine web che avevano grado \(k\) era approssimatamente proporzionale a \(\frac{1}{k^2}\).
Questi risultati ci portano a pensare che nelle reti sociali ci sono molti più nodi popolari, in quanto la popolarità dei nodi non diminuisce in modo esponenziale, ma diminuisce come l'inverso di un polinomio. Una funzione di \(k\) che, al crescere di \(k\), decresce come una fissata potenza di \(k\) della forma \(1/k^2\), prende il nome di power law.
Nel corso degli anni sono state scoperte svariate relazioni che seguono delle power law. In molti casi le relazioni di tipo power law sono trovate in sistemi sociali in cui sono presenti degli esseri umani che prendono decisioni, e in cui queste decisioni hanno dei feedback diretti sul sistema sociale in questione.
Esiste un modo semplice per vedere se abbiamo dei dati che seguono una power law. Sia \(f(k)\) la frazione degli oggetti che hanno valore \(k\), e supponiamo di voler verificare se l'equazione \(f(k) = a/k^c\) riesce ad approssimare il valore di \(f(k)\) per qualche costante \(a\) e \(c\). Prendendo il logaritmo otteniamo la seguente cosa
\[\begin{split} f(k) = \frac{a}{k^c} = a \cdot k^{-c} \iff \log{f(k)} &= \log{a \cdot k^{-c}}\\ &= \log{a} + \log{k^{-c}} \\ &= \log{a} - c \cdot \log{k} \end{split}\]
Questo significa che se abbiamo una relazione di tipo power-law, allora facendo il plot della funzione \(\log{f(k)}\) rispetto a \(\log k\), dovremmo vedere una retta in cui \(-c\) è la pendenza, e \(\log a\) è il termine noto.
Questi plots vengono chiamati log-log plots e sono uno strumento molto utile da tenere in mente. Segue un log-log plot ripreso dall'articolo linkato prima che descrive la relazione tra il grado di una pagina e il numero di pagine con quel particolare grado.
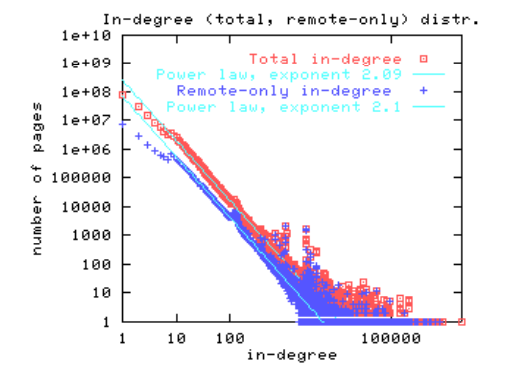
Andiamo adesso a descrivere un nuovo modello che riesce a modellare la popolarità tramite una power law.
1.3 Modello Copia
In questo nuovo modello introduciamo il concetto di temporizzazione nella creazione dei nodi e degli archi. In particolare i nuovi nodi guardano la struttura della rete prima di entrare a farne parte.
Formalmente il modello è descritto come segue: Si fissa un parametro \(p \in [0, 1]\) e si genera il primo nodo. Il processo di creazione del nodo \(i\) -esimo, per \(i \geq 2\), è il seguente
Il nodo \(i\) sceglie in modo uniforme un nodo tra tutti i nodi già presenti.
Con probabilità \(p\) il nodo \(i\) si collega al nodo scelto.
Con probabilità \(1-p\) il nodo \(i\) si collega al nodo puntato dal nodo scelto.
Andiamo adesso a calcolare la probabilità che ci sia un arco tra il nodo \(i\) e il nodo \(j\). A tale fine definiamo la seguente v.a.
\[\forall i < j: \,\, a_{i, j} = \begin{cases} 1 \,\,\, , \,\,\, j \to i \\ 0 \,\,\, , \,\,\, \text{ else } \end{cases}\]
Notiamo che \(i < j\) in quanto il nodo \(j\) si può collegare al nodo \(i\) solamente se \(i\) già esiste. Troviamo quindi la seguente espressione
\[P(a_{i, j} = 1) = p \cdot \frac{1}{j - 1} + (1 - p) \cdot \frac{\sum_{h = 1}^{j-1} a_{i, h}}{j-1}\]
Notiamo che, a differenza del modello di Erdős-Rényi, in cui la probabilità di creazione di un arco tra due nodi era sempre data dal parametro \(p\), indipendentemente dal grado dei nodi in questione, in questo nuovo modello la probabilità che \(j\) sia collegato ad \(i\) contiene il fattore \(\sum_{h = 1}^{j-1} a_{i, h}\), ed è quindi proporzionale al grado di \(i\).
Osservazione: A seguire qualche osservazione
È possibile dimostrare che \[\sum_{i = 1}^{j - 1} P(a_{i, j} = 1) = 1\]
Se \(p = 0\), la scelta dei nodi è sempre viene sempre fatta in funzione della popolarità. Se invece \(p = 1\), allora la scelta viene sempre fatta in modo indipendente dalla popolarità dei nodi, e il modello si riduce quindi al modello di Erdős-Rényi con l'aggiunta della temporizzazione. Da questo segue che il modello appena introdotto è una generalizzazione del modello di Erdős-Rényi.
La stabilità della popolarità in una rete sociale dipende molto dalle condizioni inziali. Per ulteriori approfondamenti è possibile leggere il seguente articolo, chiamato Experimental Study of Inequality and Unpredicatbility in an Artificial Cultural Market.
1.3.1 Dimostrazione Power Law
Siamo adesso interessati a far vedere che questo nuovo modello definito esibisce una power law, ovvero che il numero di nodi che hanno grado \(k\) decresce in modo polinomiale rispetto a \(k\).
Dato però che è molto difficile far vedere questa relazione per il modello esatto descritto, quello che faremo sarà modificare il modello originale per ottenere due modelli approssimati, uno discreto e l'altro continuo. Faremo poi vedere che la relazione di power law è valida per il modello continuo. Un risultato analogo è stato comunque dimostrato per il modello originale.
A tale fine definiamo la seguente quantità,
\[A_j(t) := \text{numero di in-links del nodo } j \text{ al passo } t \,\,\, , \,\,\, j \leq t\]
Dal modello originario otteniamo che \(A_j(j) = 0\) e anche che,
\[\begin{split} P(A_j(t+1) - A_j(t) = 1) &= P(t + 1 \to j) \\ &= \frac{p}{t} + \frac{a-p}{t} \cdot A_j(t) \end{split}\]
Il primo modello che approssima il modello originale, quello discreto, è definito dalla funzione discreta \(X_j(t)\), \(t \in \mathbb{N}\), nel seguente modo
\(X_j(j) = 0\)
\(\displaystyle{X_j(t+1) - X_j(t) = \frac{p}{t} + \frac{a-p}{t} \cdot X_j(t)}\)
Il modello discreto appena descritto è stato ottenuto imponendo il valore della probabilità del modello originario come valore deterministico della variazione del numero di archi entranti in \(j\) tra il passo \(t\) e il passo \(t+1\).
Dato però che è difficile lavorare con funzioni discrete, facciamo una ulteriore approssimazione introducendo un nuovo modello, questa volta continuo, definito dalla funzione continua \(x_j(t)\), \(t \in \mathbb{R}\), nel seguente modo
\(x_j(j) = 0\)
\(\displaystyle{x_j(t+1) - x_j(t) = \frac{p}{t} + \frac{1-p}{t} \cdot x_j(t)}\)
Da adesso in poi siamo interessati ad esprimere in forma chiusa la funzione \(x_j(t)\). A tale fine notiamo che l'equazione che descrive la variazione tra \(x_j(t+1)\) e \(x_j(t)\) può essere approssimata tramite la seguente equazione differenziale
\[\frac{d \,\, x_j(t)}{d \,\, t} = \frac{p}{t} + \frac{1-p}{t} \cdot x_j(t)\]
Tale E.D. è facilmente risolvibile, in quanto è una E.D. del primo ordine a variabili separabili. Procediamo quindi impostando i due integrali,
\[\require{cancel} \begin{split} \frac{d \,\, x_j(t)}{dt} = \frac{p}{t} + \frac{1-p}{t} \cdot x_j(t) &\iff \frac{d \,\, x_j(t)}{dt} = \Big(p + (1 - p) \cdot x_j(t)\Big) \cdot \frac1t \\ &\iff \frac{1}{\Big(p + (1 - p) \cdot x_j(t)\Big)} \cdot \frac{d \,\, x_j(t)}{dt} = \frac1t \\ &\iff \int \frac{1}{\Big(p + (1 - p) \cdot x_j(t)\Big)} \cdot \frac{d \,\, x_j(t)}{\cancel{dt}} \cdot \cancel{dt} = \int \frac1t dt \\ &\iff \int \frac{1}{\Big(p + (1 - p) \cdot x_j(t)\Big)} \cdot d \,\, x_j(t) = \int \frac1t dt \\ \end{split}\]
Per risolvere l'integrale del lato sinistro effettuiamo un cambiamento di variabili, introducendo \(z := p + (1-p) \cdot x_j(t)\). Otteniamo quindi,
\[dz = (1-p) d \,\, x_j(t) \iff d \,\, x_j(t) = \frac{dz}{1-p}\]
sostituendo nel primo integrale troviamo
\[\begin{split} \int \frac{1}{\Big(p + (1 - p) \cdot x_j(t)\Big)} \cdot d \,\, x_j(t) &= \int \frac1z \cdot \frac{dz}{1-p} \\ &= \frac{\ln z}{p-1} + C_1\\ &= \frac{1}{p-1} \cdot \Big[ \ln{(p + (p-1) \cdot x_j(t))}\Big] + C_1\\ \end{split}\]
Per il secondo integrale troviamo
\[\int \frac1t dt = \ln t + C_2\]
Mettendo tutto assieme siamo in grado di esplicitare \(x_j(t)\) nel seguente modo
\[\begin{split} &\;\;\;\;\;\;\;\;\;\;\; \frac{1}{p-1} \cdot \Big[ \ln{(p + (p-1) \cdot x_j(t))}\Big] + C_1 = \ln t + C_2 \\ &\iff \frac{1}{p-1} \cdot \Big[ \ln{(p + (p-1) \cdot x_j(t))}\Big] = \ln t + C\\ &\iff \Big[ \ln{(p + (p-1) \cdot x_j(t))}\Big] = (1-p) \cdot \ln t + C\\ &\iff \Big[ \ln{(p + (p-1) \cdot x_j(t))}\Big] = \ln t^{1-p} + C\\ &\iff \Big[ \ln{(p + (p-1) \cdot x_j(t))}\Big] = \ln t^{1-p} + \ln H\\ &\iff \Big[ \ln{(p + (p-1) \cdot x_j(t))}\Big] = \ln{t^{1-p} \cdot H}\\ &\iff p + (p-1) \cdot x_j(t) = H \cdot t^{1-p} \\ \end{split}\]
Dall'ultima equazione siamo in grado di esplicitare \(x_j(t)\), trovando la seguente
\[x_j(t) = \frac{H \cdot t^{1-p} - p}{1 - p}\]
dove \(H\) è una costante tale che \(C = \ln H\). Per trovare il valore di tale costante ci basta imporre la condizione iniziale, che ci dice che
\[\begin{split} x_j(j) = 0 &\iff \frac{H \cdot t^{1-p} - p}{1 - p} = 0 \\ &\iff H = \frac{p}{j^{1-p}} \\ \end{split}\]
Sostituendo il valore di \(H\) trovato nella formula chiusa di \(x_j(t)\) troviamo quindi
\[x_j(t) = \frac{p}{j^{1-p}} \cdot \frac{t^{1-p}}{1-p} - \frac{p}{1-p} \iff x_j(t) = \frac{p}{1-p} \cdot \Big[ \Big(\frac{t}{j}\Big)^{1-p} -1 \Big]\]
Ora che siamo in grado di calcolare il numero di nodi di grado \(k\), possiamo procedere nel nostro intento, che è quello di calcolare la frazione di nodi di grado \(k\). A tale fine definiamo,
\(\Gamma(k, t) := \text{ numero nodi con grado entrante } \geq k \text{ al tempo } t\)
Utilizzando la funzione \(x_j(t)\) sappiamo che, nel modello continuo,
\[\Gamma(k, t) = |\{j : \,\, x_j(t) \geq k\} |\]
Impostando e risolvendo la relativa disuguaglianza otteniamo che
\[\begin{split} &x_j(t) \geq k \\ &\iff \frac{p}{1-p} \cdot \Big[ \Big(\frac{t}{j}\Big)^{1-p} -1 \Big] \geq k \\ &\iff \Big(\frac{t}{j}\Big)^{1-p} \geq k \cdot \frac{1-p}{p} + 1 \\ &\iff \frac{t}{j} \geq \Big( k \cdot \frac{1-p}{p} + 1 \Big)^{\frac{1}{1-p}} \\ &\iff j \leq t \cdot \Big( k \cdot \frac{1-p}{p} + 1 \Big)^{-\frac{1}{1-p}} \\ \end{split}\]
Possiamo quindi approssimare \(\Gamma(k, t)\) con la seguente funzione continua
\[\Gamma(k, t) = t \cdot \bigg[ \frac{1-p}{p} \cdot k + 1 \bigg]^{-\frac{1}{1-p}}\]
Procediamo definendo quindi calcolando la funzione \(F(k)\), il cui valore è definito come la frazione dei nodi che hanno grado \(\geq k\). Dal calcolo di \(\Gamma(k, t)\) effettuato prima segue che
\[F(k) = \frac{\Gamma(k, t)}{t} = \bigg[ \frac{1-p}{p} \cdot k + 1 \bigg]^{-\frac{1}{1-p}}\]
Infine, denotando che \(f(k)\) la frazione di nodi di grado \(k\), troviamo che
\[f(k) = F(K) - F(k+1) = -\bigg[\frac{F(k+1) - F(k)}{1} \bigg] \approx - \frac{d F(k)}{k}\]
Dunque possiamo approssimare \(f(k)\) con la seguente funzione
\[f(k) \approx \frac{1}{p} \cdot \bigg[ \frac{1-p}{p} \cdot k + 1\bigg]^{-\frac{1}{1-p} -1}\]
Notiamo come \(f(k)\), che è proprio la funzione che cercavamo, ovvero la frazione di nodi di grado \(k\), decresce come \(k^{-c}\), dove \(c\) è una costante ottenuta in funzione di \(p\), che vale \(-2\), quando \(p = 0\).
Concludiamo quindi osservando che il modello sintetico definito esibisce una power law rispetto alla popolarità dei nodi, e quindi si avvicina alle reti sociali di più del modello di Erdős-Rényi.
2 Amazon e la Lunga Coda
Supponiamo di considerare i magazzini di Amazon, in cui ci sono tanti articoli di nicchia, ciascuno dei quali vende pochi pezzi, e pochi articoli di punta, ciascuno dei quali vende tanti pezzi. Ci poniamo quindi la seguente domanda: Amazon guadagna di più vendendo le poche merci più famose, oppure vendendo le tante marci di nicchia?
Per cercare di rispondere a tale domanda definiamo la seguente funzione
\[f(k) := \text{ numero di oggetti che vengono acquistati da } k \text{ persone}\]
Supponiamo che \(f(k)\) e \(k\) sono correlate dalla seguente power law, \(f(k) = k^{-2}\). Troviamo quindi il seguente grafico,

Per rispondere alla nostra domanda però non siamo interessati ad \(f(k)\). Siamo invece interessati alla funzione inversa \(k = f^{-1}(n) = \frac{1}{\sqrt{n}}\), che ci dice il numero di vendite dell'\(n\) esimo oggetto più popolare. Per la funzione inversa quindi abbiamo il seguente grafico,
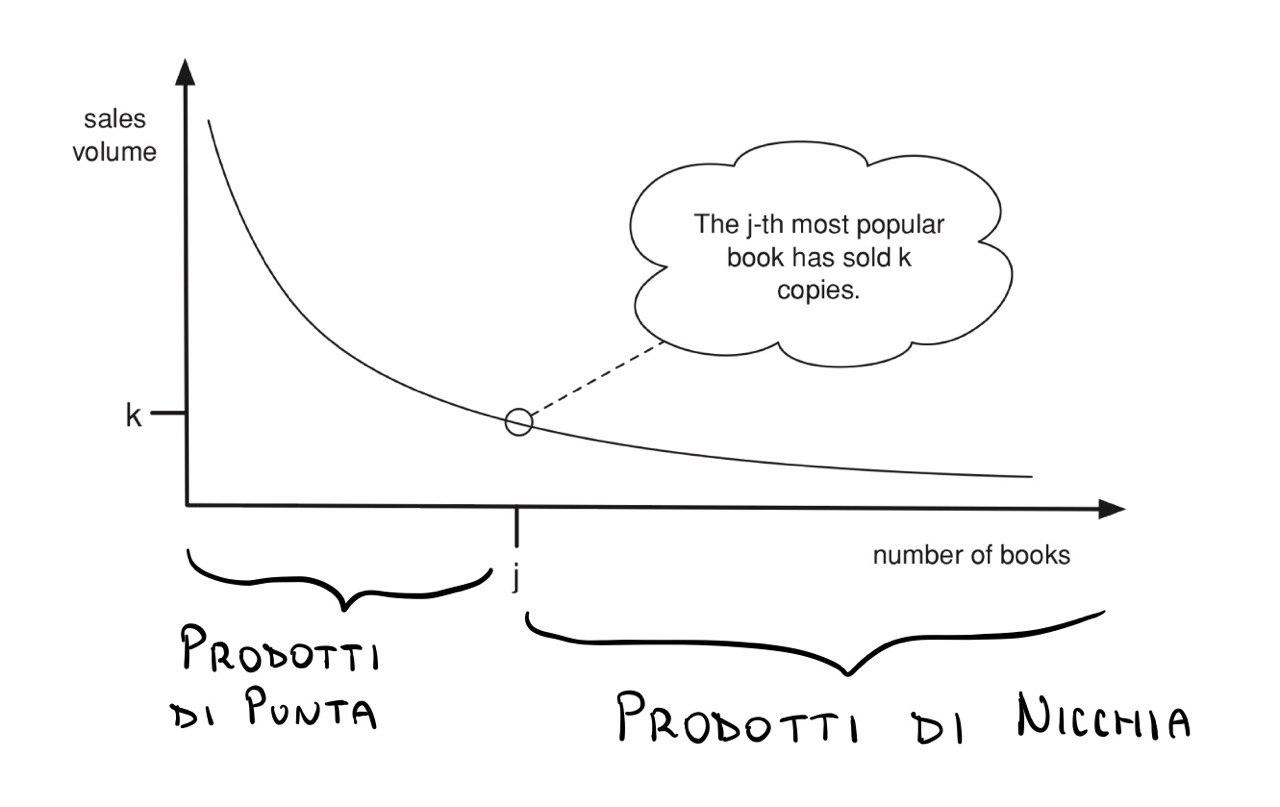
Notiamo che l'area sotto la curva approssima il valore del guadagno totale. È possibile far vedere che l'area sotto la curva nella coda della funzione in questione risulta essere una frazione significativa del totale valore dell'area, anche se si inizia a considerare l'area a partire da un valore \(j_0\) che si trova abbastanza spostato a destra rispetto all'origine.
Questo fenomeno prende il nome di lunga coda, e nel contesto di Amazin significa che le merci di nicchia sono importanti tanto quanto quelle non di nicchia.
Tramite i sistemi di raccomandazione poi, Amazon è in grado di rendere questo fenomeno più o meno potente, a seconda dei propri obiettivi.