AR - 14 - Processi di Diffusione III
Lecture Info
Data:
Capitolo Libro: Chapter 19 - Cascading Behavior in Networks
Introduzione: In questa lezione abbiamo terminato la discussione sui processi di diffusione. In particolare abbiamo analizzato il caso del bilinguismo, in cui la nuova tecnologia poteva essere adottata assieme a quella vecchia, pagando però un costo di mantenimento. In questo nuovo contesto abbiamo analizzato la capacità della rete quando la topologia della rete è un semplice cammino.
1 Bilinguismo
Fino ad adesso abbiamo assunto che i prodotti \(A\) e \(B\) sono prodotti mutualmente esclusivi, ovvero che una scelta esclude l'altra. Esistono però svariate situazioni in cui \(2\) prodotti possono coesistere.
Un esempio chiave per capire questo fenomeno ci è offerto dal bilinguismo, ripreso dal dominio della lingua. In particolare un individuo è portato a parlare due lingue diverse solamente quando un po' dei suoi vicini parlano la prima lingua, diciamo \(A\), e un altro po' dei suoi vicini parlano un'altra lingua, diciamo \(B\).
Questa situazione in cui ogni individuo non solo può sceglire tra \(A\) e \(B\), ma può anche scegliere di usare sia \(A\) che \(B\) è quindi descritta dal seguente gioco
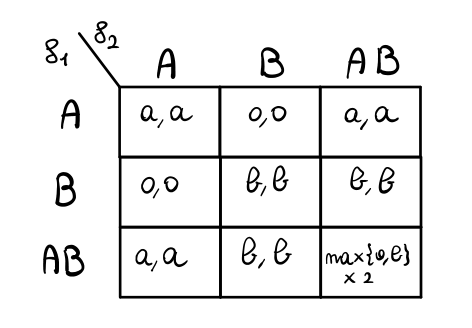
Nella matrice è stato omesso il costo nell'adottare la strategia \(AB\). Tale costo sarà indicato con \(c\).
Andiamo adesso a vedere il guadagno di un giocatore, considerando che il gioco appena descritto viene giocato per ogni nodo adiacente al giocatore considerato. Sia quindi \(v \in V\) un nodo. Troviamo che,
Se \(v\) sceglie \(A\), allora \(v\) potrà parlare solamente con i vicini che parlano \(A\) o \(AB\), e quindi il suo guadagno sarà dato da
\[a \cdot | N_{A}(v) \cup N_{AB}(v) |\]
Se \(v\) sceglie \(B\), allora \(v\) potrà parlare solamente con i vicini che parlano \(B\) o \(AB\), e quindi il suo guadagno sarà dato da
\[b \cdot | N_{B}(v) \cup N_{AB}(v) |\]
Se \(v\) sceglie \(AB\), allora \(v\) potrà parlare sia con i vicini che parlano \(A\), sia con i vicini che parlano \(B\), e sia con i vicini che parlano \(AB\). Per mantenere il bilinguismo \(AB\) però il nodo \(v\) dovrà anche pagare un fattore \(c\). Il suo guadagno è quindi dato da
\[ a \cdot |N_{A}(v)| + b \cdot |N_{B}(v)| + \max\{a, b\} \cdot |N_{AB}(v)| - c\]
È dunque intuibile che per capire se conviene o meno adottare il bilinguismo bisogna considerare il costo \(c\) per poterlo mantenere. In particolare, è possibile dimostrare che se \(c\) è piccolo, allora vince il bilinguismo. Detto questo, anche la vittoria tra \(A\) e \(B\) dipende dal valore di \(c\). Infatti è possibile dimostrare che \(A\) prende piede se \(c\) è molto piccolo o se \(c\) è molto grande. Esiste quindi una fascia intermedia in cui la scelta vecchia \(B\) risulta essere quella più effettiva.
2 Capacità nella Catena con Bilinguismo
Andiamo adesso a vedere i risultati descritti prima nel particolare caso del cammino. Consideriamo quindi un grafico con la seguente topologia e supponiamo di aver un solo initiator \(v\) che adotta la nuova scelta \(A\).
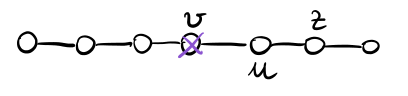
Per semplificare la nostra analisi possiamo considerare \(b\) la nostra unità di misura ponendo \(b=1\) e rapportare con \(b\) i valori che otteniamo per gli altri due parametri \(a\) e \(c\). Notiamo che questa scelta è molto comoda, in quanto ci permette di visualizzare le relazioni tra \(a\) e \(c\) nel piano cartesiano.
Consideriamo adesso il nodo \(u \in V\). Definiamo con \(r(u)\) il guadagno del nodo \(u\). Abbiamo quindi i seguenti casi
Se \(u \to A\), ovvero se \(u\) passa ad \(A\) allora \(r(u) = a\).
Se \(u \to B\), allora allora \(r(u) = 1\).
Se \(u \to AB\), allora \(r(u) = a + 1 - c\).
Per capire la scelta migliore del nodo \(u\) confrontiamo coppia a coppia le possibili scelte per ottenere
"meglio \(A\) che \(B\) " \(\iff a \geq 1\)
"meglio \(A\) che \(AB\) " \(\iff a \geq a + 1 - c \iff c \geq 1\)
"meglio \(B\) che \(AB\) " \(\iff 1 \geq a + 1 - c \iff c \geq a\)
Queste relazioni possono essere rappresentate nel piano cartesiano come segue.
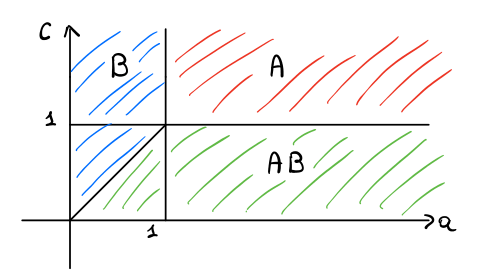
dove,
Nella zona vince \(A\), in quanto
\(\begin{cases} a \geq 1 &\implies A > B \\ c \geq 1 &\implies A > AB \end{cases}\)
Nella zona vince \(B\), in quanto
\(\begin{cases} a < 1 &\implies B > A \\ c \geq a &\implies B > AB \end{cases}\)
Nella zona vince \(AB\), in quanto
\(\begin{cases} c < 1 &\implies AB > A \\ c < a &\implies AB > B \end{cases}\)
Semplificando troviamo quindi il seguente schema,
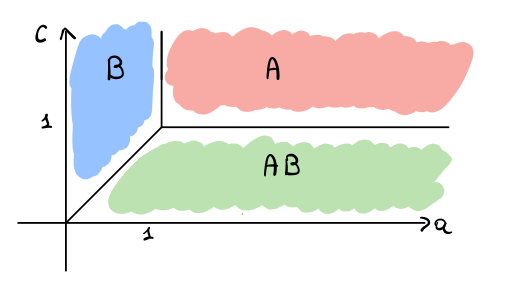
A seconda del valore dei parametri \(a\) e \(c\), al nodo \(u\) potrà convenire una scelta tra \(A\), \(B\) e \(AB\). Per quanto riguarda l'innesco di una cascata, notiamo che
Se ci troviamo in \(A\), allora la cascata parte sempre, in quanto i parametri \(c\) e \(a\) sono fissati, e dunque il nodo \(z\) si troverà nella stessa situazione di \(u\).
Se ci troviamo in \(B\), la cascata non parte, in quanto il processo è già bloccato.
Se ci troviamo nella regione \(AB\), non possiamo dire ancora nulla rispetto.
Resta quindi da studiare il comportamento di \(z\) quando ci troviamo nella regione \(AB\).
Per analizzare il restante caso supponiamo che \(u\) scelga \(AB\). La situazione è quindi la seguente
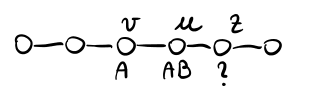
Come abbiamo fatto per \(u\), andiamo adesso ad analizzare le possibili scelte di \(z\) con i relativi guadagni,
\[r(z) = \begin{cases} a \,\,\, &, \,\,\, z \to A \\ 2 \,\,\, &, \,\,\, z \to B \\ \max\{a, 1\} + 1 - c\,\,\, &, \,\,\, z \to AB \\ \end{cases}\]
Dato che abbiamo supposto che \(u \in AB\), consideriamo solo la porzione verde del piano mostrato prima in cui vince \(AB\). Per poter effettuare l'analisi sulla scelta migliore per il nodo \(z\), dobbiamo analizzare due sottocasi: uno in cui \(a \leq 1\), e l'altro in cui \(a > 1\).
Sottocaso 1: \(a \leq 1\)
Siamo adesso in grado di calcolare il guadagno di \(z\) se sceglie \(AB\), che è pari a \(r(z) = 2 - c\). Dunque troviamo,
"\(A\) meglio di \(B\) " \(\implies a \geq 2\)
"\(B\) meglio di \(AB\) " \(\implies 2 \geq 2 - c\)
Notiamo quindi che \(A\) non sarà mai meglio di \(B\) in questo caso, e che \(B\) è sempre meglio di \(AB\). Dunque in questa sottoregione, quando \(a \leq 1\) abbiamo che \(B\) vince sempre.
Sottocaso 2: \(a > 1\)
Questa volta se \(Z \to AB\), allora il guadagno di \(z\) è \(r(z) = a + 1 - c\). Troviamo quindi le seguenti possibilità
"\(A\) meglio di \(B\) " \(\implies a \geq 2\)
"\(A\) meglio di \(AB\) " \(\implies a > a + 1 - c \iff c > 1\)
"\(B\) meglio di \(AB\) " \(\implies 2 \geq a + 1 - c \iff c \geq a - 1\)
In questo caso quindi abbiamo che quando \(a < 1\) conviene sempre \(B\). Esiste però anche un'altra regione in cui conviene \(B\), questa regione è la regione del piano in cui \(c \in (a - 1, 1)\). Mettendo tutte queste informazioni assieme troviamo quindi il seguente grafico per la scelta di \(z\)
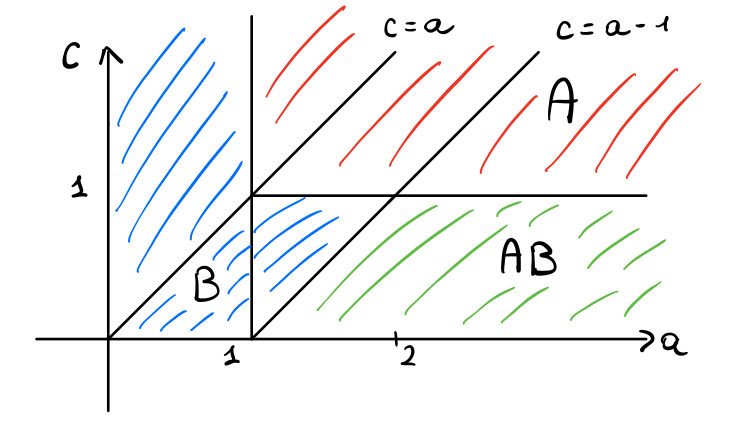
Andando poi a rimuovere dettagli superflui, troviamo il seguente schema
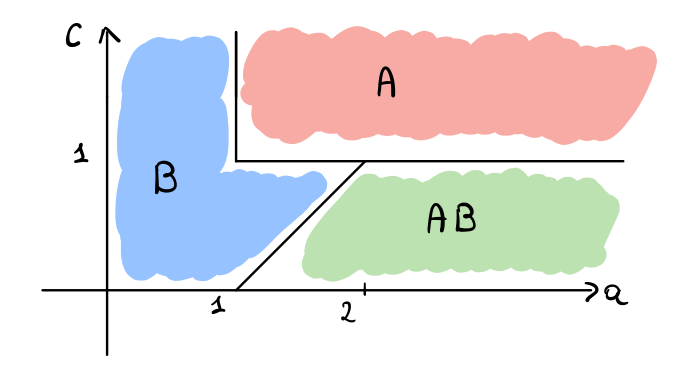
Concludiamo con qualche nota finale:
Può succedere che il nodo \(u\) scelga il bilinguismo \(u \to AB\), ma non è comunque in grado di convincere il nodo \(z\) a passare anche lui ad \(AB\).
Una volta che \(u\) convince \(z\) a passare ad \(AB\), il nodo \(u\) può lasciare \(AB\) per prendere \(A\). Questa dinamica poi viene ripetuta anche da \(z\), finendo quindi per innescare una catena. Il fatto che il bilinguismo non dura molto è una conseguenza particolare della topologia in questione (il cammino).
Come è possibile vedere, \(A\) prende piede quando \(c > 1\). Notiamo però che \(B\) dura anche quando \(a \in [1, 2]\) e \(c \in [a-1, 1]\), ovvero quando \(c\) non è molto più piccolo di \(a\), e quindi non conviene pagare il bilinguismo.