AR - 18 - Sistemi di Voto II

Lecture Info

Data: [2018-12-17 lun]
Capitolo Libro: Chapter 23 - Voting
Introduzione: In questa lezione abbiamo introdotto alcune delle caratteristiche che un sistema di voto "buono" dovrebbe avere. Abbiamo poi dimostrato il Teorema di Arrow, che ci dice che l'unico sistema di voto "buono" è la dittatura. Infine, siamo andati oltre Arrow per capire alcune caratteristiche dei sistemi di voto nella realtà.

1 Principi per Sistemi di Voto

La scorsa lezione abbiamo introdotto due particolari sistemi di voto, e abbiamo fatto vedere che entrambi i sistemi di voto avevano i propri problemi. Iniziamo questa lezione discutendo le caratteristiche che un sistema di voto $F$ "buono" dovrebbe avere.

1.1 PIIA - Indipendenza Alternative Irrilevanti

Intuitivamente diciamo che un sistema di voto $F$ rispetta il principio PIIA, o anche indipendenza dalle alternative irrilevanti, se nessun partecipante può cambiare alcune delle sue preferenze in modo strategico al fine di cambiare l'ordinamento aggregato calcolato da $F$. Andiamo adesso a formalizzare tale idea.

Formalmente diciamo che $F$ rispetta PIIA se, dato un profilo $P = \{r_1, r_2, ..., r_k\}$, e date due alternative $y, z \in N$, con $F(P)(y) > F(P)(z)$, per ogni profilo $P' = \{r_1', r_2', ..., r_k'\}$ tale che per ogni $i = 1,...,k$ si ha che $r_i'(y) > r_i'(z) \iff r_i(y) > r_i(z)$, allora

\[F(P')(y) > F(P')(z)\]

1.2 PU - Principio di Unanimità

Intuitivamente $F$ rispetta il principio PU, o anche principio di unanimità, se le scelte prese in modo unanime vengono riportate nel voto aggregato finale.

Formalmente, $F$ rispetta PU se per ogni profilo $P = \{r_1, ..., r_k\}$ tale che esistono due alternative $y, z$ su cui tutti i votanti pensano che $r_i(y) > r_i(z), \,\, i = 1, ..., k$, allora

\[F(P)(y) > F(P)(z)\]

2 Teorema di Arrow

Se le alternative di voto sono solamente $2$, $|N| = 2$, allora sia il voto a maggioranza sia quello posizionale funzionano bene. I problemi però escono fuori quando $|N| \geq 3$. Infatti è possibile dimostrare, e sarà il focus di questa sezione, che l'unico sistema di voto che rispetta i principi PIIA e PU è la dittatura. Tale risultato di (impossibilità) di avere un buon sistema di voto al di fuori della dittatura prende il nome di Teorema di (impossibilità) di Arrow.

Teorema di Arrow: Se $|N| > 3$, per ogni sistema di voto $F: \Pi(N)^k \to \Pi(N)$ tale che $F$ soddisfa PIIA e PU, si ha che

\[\exists j \in \{1, ..., k\}: \,\,\, \forall \,\,\, \text{profilo } P: \,\,\, F(P) = r_j\]

Il teorema di Arrow ci dice che ogni sistema di voto che soddisfa PU e PIIA ammette sempre l'esistenza di un dittatore, ovvero di un individuo le cui singole preferenze combaciano son le preferenze aggregate. Per valere il teorema richiede solamente che il numero dei votanti sia fissato.

Al fine di dimostrare il teorema di Arrow introduciamo la seguente definizione

Definizione: Dato un profilo $P$, diciamo che l'alternativa $x \in N$ è polarizzante per $p$ se per ogni votante $i = 1,...,k$ si ha che $x$ è votato come ultimo da $i$, $r_i(x) = 0$, oppure $x$ è votato come primo da $i$, $r_i(x) = n-1$.

Segue un lemma tecnico che sarà utilizzato per la dimostrazione del teorema.

Lemma: Sia $|N| \geq 3$, e sia $F$ un sistema di voto che soddisfa PU e PIIA. Allora per ogni profilo $P$ tale che esiste un $x$ polarizzante per $P$, si ha che o $x$ è ultimo nel risultato aggregato $F(P)(x) = 0$, oppure $x$ è primo nel risultato aggregato $F(P)(x) = n-1$.

Il lemma essenzialmente ci dice che le alternative polarizzanti, se si utilizza un "buono" sistema di voto, arrivano nella graduatoria finale sempre o in prima o in ultima posizione. Procediamo quindi con la dimostrazione del lemma.

Dimostrazione: Supponiamo per assurdo che $x$ è polarizzante per $P$, e che però $x$ non arriva né primo né ultimo in graduatoria finale, ovvero che esistono altre due alternative $y, z \in N$, tali che

\[F(P)(Y) > F(P)(X) > F(P)(Z)\]

A partire da $P$ ci costruiamo un nuovo profilo $P'$ come segue: $P'$ è uguale a $P$, tranne che per il ranking assegnato dai vari votanti all'alternativa $z$. In particolare vale la seguente cosa

\[\forall i: \,\, r_i(y) > r_i(z) \implies r_i'(z) = r_i'(y) + 1\]

Questo significa che $P'$ è ottenuto prendendo $P$ e spostando $z$ sopra ad $y$. A questo punto notiamo che l'ordine relativo di ciascun votante rispetto a $x$ e $y$ non cambia quando passo da $P$ a $P'$. La stessa cosa vale per $x$ e $z$. Ma allora, dato che $F$ soddisfa PIIA, trovo che

\[\begin{cases} F(P')(y) > F(P')(x) \\ F(P')(x) > F(P')(z) \end{cases} \implies F(P')(y) > F(P')(x) > F(P')(z) \]

Per concludere la dimostrazione, osserviamo che in $P'$ $z$ sta sempre davanti a $y$, e quindi, dato che $F$ soddisfa PU, bisogna avere

\[F(P')(z) > F(P')(y)\]

$\Huge\unicode{x21af}$.

Siamo ora in grado di procedere con la dimostrazione del teorema di Arrow.

2.1 Dimostrazione Teorema Arrow

L'idea alla base della dimostrazione è quella di utilizzare un certo numero di profili appositamente costruiti al fine di testare il sistema di voto $F$ che ci viene dato. Vedendo come $F$ risponde ai profili costruiti siamo infatti in grado di capire chi è il ditattore per $F$.

Assumiamo quindi che $F$ rispetta PIIA e PU.

2.1.1 Costruzione Profili $P_i$

Sia $x \in N$ una alternativa qualsiasi.

Costruiamo il primo profilo $P_0 = \{r_1^0, r_2^0, ..., r_k^0\}$ tale che i ranking dei vari votanti hanno la seguente forma

$r_1^0 = \langle \text{ordinamento di } N - \{x\} \rangle \; x$
$r_1^0 = \langle \text{ordinamento di } N - \{x\} \rangle \; x$
$\ldots$
$r_k^0 = \langle \text{ordinamento di } N - \{x\} \rangle \; x$

Il profilo $P_1 = \{r_1^1, r_2^1, ..., r_k^1\}$ invece è costruito prendendo il profilo $P_0$ e cambiando l'opinione del primo votante rispetto all'alternativa $x$, che passa da ultimo, $r_1^0(x) = 0$, a primo, $r_1^1(x) = n-1$.

Il profilo $P_2 = \{r_1^1, r_2^1, ..., r_k^1\}$ invece è costruito prendendo il profilo $P_1$ e cambiando l'opinione del secondo votante rispetto all'alternativa $x$, che passa da ultimo, $r_2^1(x) = 0$, a primo, $r_2^2(x) = n-1$.

In generale quindi si costruiscono $k$ profili $P_1, P_2, ..., P_k$ come segue

$\forall i: \,\,\, r_i^0(x) = 0$
$\forall 1 \leq h \leq k: \,\,\, r_i^h(x) = \begin{cases} n-1 \,\,&,\,\, i \leq h \\ 0 \,\,&,\,\, i > h \\ \end{cases}$

Notiamo che per costruzione $x$ è polarizzante per ogni profilo $P_0, P_1, ..., P_k$. Ma allora, per il lemma precedentemente dimostrato, vale che

\[\forall \,\, 0 \leq h \leq k: \,\,\, F(P_h)(x) = 0 \,\,\ \lor \,\,\, F(P_h)(x) = n-1\]

Inoltre, dato che $F$ rispetta PU, abbiamo che

$\begin{cases} F(P_0)(x) = 0 \\ F(P_k)(x) = n-1 \\ \end{cases}$

2.1.2 Individuazione del ditattore

Sia ora $j$ l'indice tale che

\[j = \underset{h = 1,...,k}{\min} \{h: \,\, F(P_h)(x) = n-1\}\]

ovvero $j$ è il più piccolo indice associato ad un profilo il cui voto aggregato calcolato tramite $F$ mette $x$ al primo posto.

Osserviamo che $P_{j-1}$ e $P_j$ differiscono solo per la scelta effettuata dal votante $j$ rispetto all'alternativa $x$. Infatti si ha che

\[r_j^{j-1}(x) = 0 \,\, \land \,\, r_j^j(x) = n-1\]

si può quindi vedere come $j$ abbia tanta influenza nel proesso di votazione: cambiando la sua opinione su $x$ ha fatto passare $x$ da ultimo a primo nel voto aggregato. Questa idea è formalizzata facendo vedere che il dittatore enunciato dal teorema è proprio il votante $j$.

Formalmente quello che vogliamo dimostrare è che per ogni profilo $Q$ si ha che $F(Q) = r_j^{(Q)}$, ovvero che il voto aggregato coincide con il voto del $j$ -esimo votante. Notiamo che tale espressione può essere esplicitata come segue

\[\forall \, Q: \,\, \forall \, y, z \in N: \,\, F(Q)(y) > F(Q)(z) \iff r_j^{(Q)}(y) > r_j^{(Q)}(z)\]

La dimostrazione di questo è spezzata in tre parti.

2.1.3 Il votante $j$ è il ditattore - parte 1: $y, z \in N - \{x\}$

Sia $Q$ un profilo qualsiasi, e siano $y, z \in N - \{x\}$ due alternative diverse da $x$ tali che $r_j^{(Q)}(y) > r_j^{(Q)}(z)$. Partendo da $Q$ costruiamo un nuovo profilo $Q'$ nel seguente modo:

Per i primi $j$ votanti in $Q$, prendo $x$ e lo porto in testa.
Per i rimanenti votanti in $Q$, prendo $x$ e lo porto in coda.
Infine, per il votante $j$ -esimo, prendo $y$ e lo metto in testa ad $x$.

Graficamente quindi ottengo la seguente costruzione

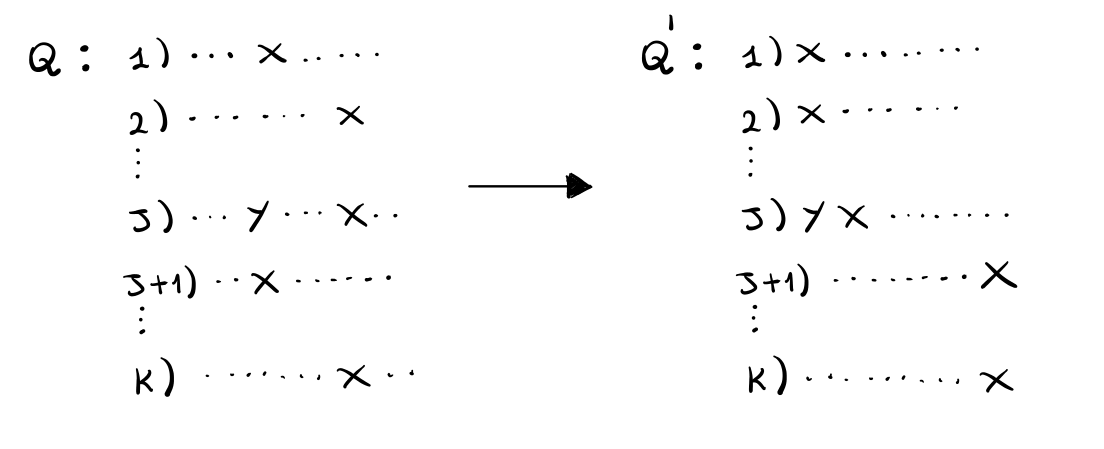
Dalla costruzione si ha che in $Q'$ le posizioni relative rispetto a varie alternative rimangono invariate da quelle in $Q$.

Confrontiamo adesso $Q'$ e $P_j$. Notiamo che l'ordine relativo di $x$ e $z$ è lo stesso per ogni votante $h=1,...,k$ nei profili $Q'$ e $P_j$. Inoltre, $F(P_j)(x) > F(P_j)(z)$ in quanto $F(P_j)(x) = n-1$. Ma allora, utilizzando il fatto che $F$ rispetta PIIA, si ha che vale la stessa cosa per $Q'$, ovvero che $F(Q')(x) > F(Q')(z)$.

Continuiamo confrontando $Q'$ e $P_{j-1}$. Questa volta è l'ordine relativo di $x$ e $y$ a rimanere invariato per ogni votante nei due profili $Q'$ e $P_{j-1}$. Inoltre $F(P_{j-1})(x) < F(P_{j-1})(y))$, in quanto $F(P_j)(x) = 0$. Ma allora, dato che $F$ rispetta PIIA, la stessa cosa vale per $Q'$, e quindi $F(Q')(x) < F(Q')(y)$.

Mettendo assieme gli ultimi due paragrafi, otteniamo che

\[F(Q')(z) < F(Q')(x) < F(Q')(y)\]

Per finire questa prima parte, confrontiamo $Q'$ con $Q$. Notiamo nuovamente che l'ordine relativo di $y$ e $z$ è lo stesso in entrambi i profili, in quanto abbiamo inizialmente assunto che $r_j^{(Q)}(y) > r_j^{(Q)}(z)$. Ma allora, dato che $F(Q')(z) < F(Q')(y)$, otteniamo che $F(Q)(y) > F(Q)(z)$.

Questo significa che per le alternative diverse da $x$, il votante $j$ effettivamente risulta essere il dittatore che stavamo cercando. Andiamo adesso a gestire il caso in cui una alternativa può essere $x$.

2.1.4 Il votante $j$ è il dittatore - parte 2: $y \in N - \{x\}, z=x$

Siano $y \in N - \{x\}$ e $z = x$ due alternative.

Per procedere in questo caso prendiamo un'altra alternativa $w \in N - \{x, y\}$ e costruiamo $k+1$ profili $\overline{P}_0, \overline{P}_1, ..., \overline{P}_k$ in modo analogo a quanto fatto inizialmente, ma questa volta rispetto a $w$. I profili costruiti possono essere rappresentati in questo modo

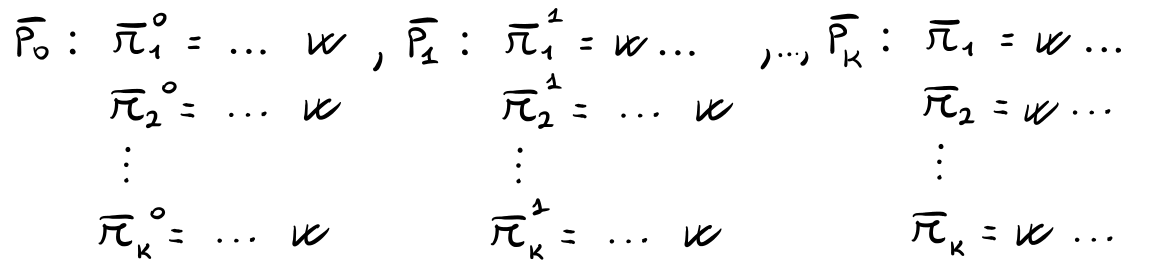
In modo analogo a quanto visto prima abbiamo che che $F(\overline{P}_0)(w) = 0$ e $F(\overline{P}_k)(w) = n-1$. Sia poi $l$ il seguente indice

\[l = \underset{h = 1,...,k}{\min} \{h: \,\, F(\overline{P}_h)(x) = n-1\}\]

Ripetendo lo stesso ragionamento svolto prima, ma questa volta utilizzando $x$ e $y$, e non $w$, otteniamo che per ogni profilo $Q$ e per ogni alternativa $y \in N - \{x\}$

\[F(Q)(x) > F(Q)(y) \iff r_l^{(Q)}(x) > r_l^{(Q)}(y)\]

Per concludere la dimostrazione ci basta dimostrare che $l=j$.

2.1.5 Il votante $j$ è il dittatore - parte 3: $l=j$

Iniziamo osservando che né $j$ né $l$ possono essere $0$, in quanto $j$ e $l$ sono votanti, e quindi appartengono all'insieme $j, l \in \{1, 2, ..., k\}$.

Confrontiamo adesso $P_{j-1}$ e $P_j$. Per costruzione sappiamo che $F(P_{j-1})(x) = 0$ e $F(P_j)(x) = n-1$. Ma allora per ogni alternativa $y \in N - \{x\}$ valgono le seguenti due cose

$\begin{cases} F(P_{j-1})(x) < F(P_{j-1})(y) \\ F(P_j)(x) > F(P_j)(y) \end{cases}$

Supponiamo per assurdo che $j \neq l$. Abbiamo due possibili casi da analizzare

$l \leq j-1$: In questo caso abbiamo che il votante $l$ nel profilo $P_{j-1}$ sceglie $x$ come primo. Ma allora,

\[\begin{split} r_l^{P_{j-1}}(x) = n-1 &\implies r_l^{P_{j-1}}(x) > r_l^{P_{j-1}}(y) \\ &\implies F(P_{j-1})(x) > F(P_{j-1})(y) \\ \end{split}\]

Dalla contraddizione segue che $l$ non può essere $\leq j-1$. $\large\unicode{x21af}$.
$l \geq j+1$: In questo caso abbiamo che il vovante $l$ nel profilo $P_j$ scegliere $x$ come ultimo. Ma allora,

\[\begin{split} r_l^{P_{j}}(x) = 0 &\implies r_l^{P_{j}}(x) < r_l^{P_{j}}(y) \\ &\implies F(P_{j})(x) < F(P_{j})(y) \\ \end{split}\]

Dalla contraddizione segue che $l$ non può essere $\geq j+1$. $\large\unicode{x21af}$.

Concludiamo che $j = l$, e che quindi è sempre possibile trovare un votante che fa da dittatore. La dimostrazione del teorema è dunque conclusa.

\[\tag*{$\blacksquare$}\]

3 Teorema del Votante Mediano

Anche se il teorema di Arrow può essere interpretato come un risultato "negativo", se si è contro la dittatura, la situazione nel mondo reale non è poi così grave. Molto spesso infatti nei sistemi di voto reali è possibile ordinare in modo graduale le varie alternative.

Esempio: Un esempio di questa gradualità è offerto dalla scelta dei college negli Stati Uniti. Possono esistere vari criteri da utilizzare per ordinare tra loro le varie alternative, tra cui: costo annuale, ranking nazionale, dimensione media delle classi.

Una conseguenza naturale nell'essere in grado di ordinare in modo graduale le varie alternative è anche anche i rankings seguono una certa regolarità. Per formalizzare matematicamente questo idea si utilizza il concetto di estremale, che indica un massimo o un minimo relativo. L'idea infatti è che una votazione, per poter essere considerata regolare, deve avere un solo estremale, che deve coincidere anche con il massimo globale.

Volendo essere più formali, molto spesso nella realtà sono verificate le seguenti condizioni

L'insieme delle alternative $N = \{x_1, x_2, ..., x_n\}$ è un insieme ordinato, con $x_1 < x_2 < ... < x_n$.
I rankings sono singled peaked, ovvero per ogni votante $i = 1, ..., k$ per ogni alternativa $j = 1, ..., n$, se $r_i(x_j) = n-1$, ovvero se l'alternativa $x_j$ è la migliore, allora

\[\begin{cases} r_i(x_h) > r_i(x_{h-1}) \,\, ,& \,\, \forall h \leq j \\ r_i(x_h) > r_i(x_{h+1}) \,\, ,& \,\, \forall h > j \\ \end{cases}\]

il che vuol dire che se consideriamo il grafico che mette in relazione il ranking che il votante $i$ da alle varie alternative, troviamo la seguente figura

Consideriamo adesso un profilo $P = \{r_1, r_2, ..., r-k\}$ e per ogni votante $i = 1,...,k$ sia $M_i \in N$ l'alternativa tale che $r_i(M_i) = n-1$, ovvero l'alternativa presa come "migliore" dal votante $i$. Andiamo adesso ad ordinare i votanti in modo tale che per ogni $i = 1,...,k$ si ha che $M_i \leq M_{i+1}$. Vale il seguente risultato.

Teorema del Votante Mediano: Se $k$ è dispari, allora per ogni $y \neq M_{\frac{k+1}{2}}$, vale che

\[|\{i : \,\, r_i(M_{\frac{k+1}{2}}) > r_i(y) \}| > |\{i: \,\, r_i(M_{\frac{k+1}{2}}) < r_i(y) \}|\]

Il teorema ci dice che dopo aver ordinato i votanti rispetto all'ordine delle alternative migliori, l'alternativa scelta come migliore dal votante mediano è quella che batte tutte le altre alternative, e quindi può essere scelta come quella migliore in assoluto.

Come conseguenza del teorema inoltre abbiamo che sotto queste ipotesi, il sistema di voto a maggioranza è quello migliore, in quanto non vale più il paradosso di condorcet, visto nella scorsa lezione.

Procediamo quindi con la dimostrazione del teorema, ricordando prima di iniziare di aver ordinato i vari votanti $i = 1,...,k$ in modo tale che $M_i \leq M_{i+1}$.

Dimostrazione: Sia $x_t > M_{\frac{k+1}{2}}$. Il caso rimanente $x_t < M_{\frac{k+1}{2}}$ è trattato in modo simmetrico.

Consideriamo un generico votante $i$ che si trova prima del votante mediano, $i \leq \frac{k+1}{2}$. Rappresentando graficamente il ranking assegnato da $i$ alle varie alternative troviamo il seguente grafico

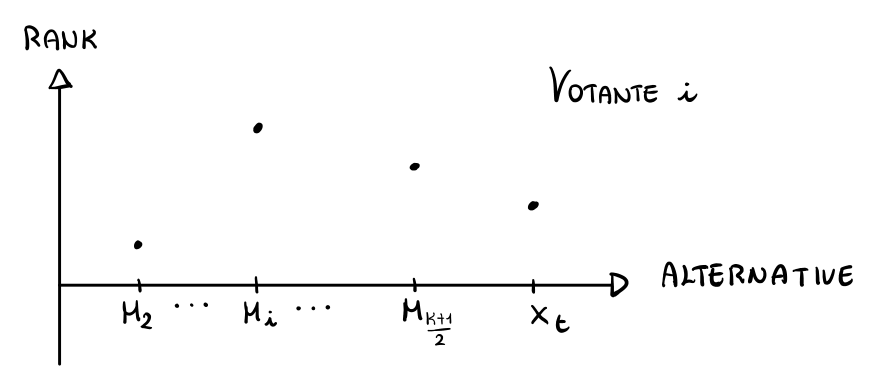
Dal grafico si vede che $r_i(M_{\frac{k+1}{2}}) > r_i(x_t)$. Più in generale vale la seguente cosa

\[\forall i \leq \frac{k+1}{2}: \,\,\,\, r_i(M_{\frac{k+1}{2}}) > r_i(x_t)\]

il che equivale a dire che tutti i votanti che si trovano prima del votante mediano $(k+1)/2$ preferiscono $M_{\frac{k+1}{2}}$ a $x_t$, in quanto la scelta "migliore" per questi votanti si trova a sinistra di $M_{\frac{k+1}{2}}$. Ma allora abbiamo che

\[|\{i: \,\, r_i(M_{\frac{k+1}{2}}) > r_i(x_t)\}| \geq \frac{k+1}{2}\]

e quindi, dato che più della metà dei votanti preferiscono $M_{\frac{k+1}{2}}$ a $x_t$, abbiamo che $M_{\frac{k+1}{2}}$ batte $x_t$ in un sistema di voto a maggioranza.

Per concludere, ci basta osservare che il ragionamento appena ripotato può essere fatto per tutte le alternative $x_t \neq M_{\frac{k+1}{2}}$, sia che $x_t > M_{\frac{k+1}{2}}$ e sia che $x_t < M_{\frac{k+1}{2}}$ (in quest'altro caso consideriamo tutti i votanti a destra di $(k+1)/2$), concludiamo che $M_{\frac{k+1}{2}}$ è l'alternativa che batte tutte le altre.

\[\tag*{$\blacksquare$}\]

3.1 Esempio

Consideriamo $5$ alternative $x_1, x_2, ..., x_5$ ordinate tali che $x_i < x_{i+1}$, e consideriamo $3$ giudici che votano come segue

Votante 1: Il primo votante sceglie il seguente ranking $x_5 < x_4 < x_3 < x_2 < x_1$, che possiamo mostrare graficamente come segue

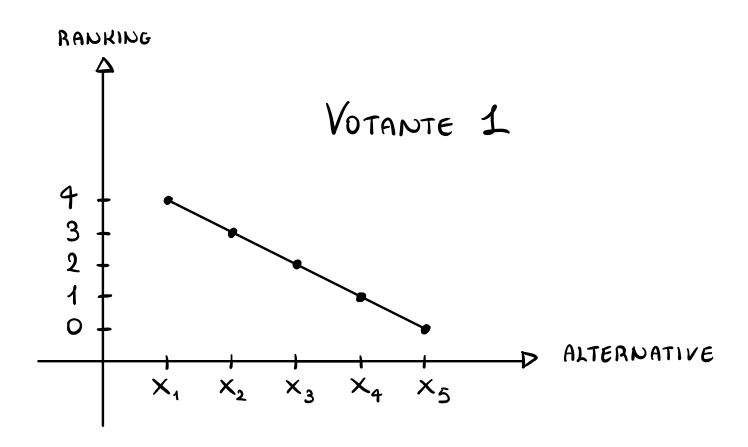
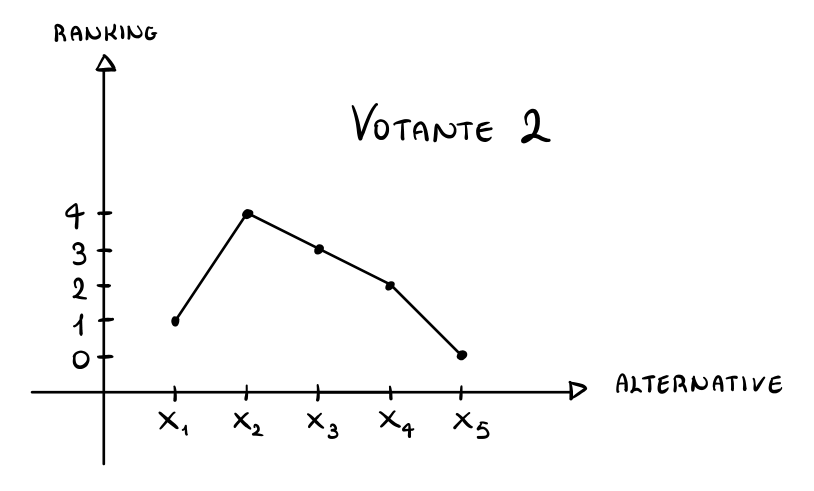
Votante 2: Il primo votante sceglie il seguente ranking $x_5 < x_1 < x_4 < x_3 < x_2$, che possiamo mostrare graficamente come segue

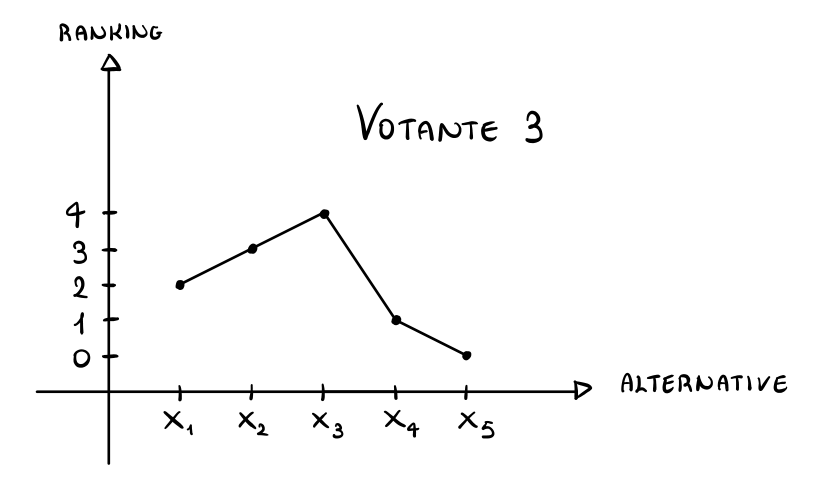
Votante 3: Il primo votante sceglie il seguente ranking $x_5 < x_4 < x_1 < x_2 < x_3$, che possiamo mostrare graficamente come segue

Per ottenere un ranking aggregato possiamo utilizzare il teorema del votante medio come segue:

Cominciamo calcolando i vari "peaks", ovvero le scelte migliori per i vari votanti, che in questo caso sono $M_1 = x_1, M_2 = x_2, M_3 = x_3$. Notiamo che i vari peaks sono già ordinati tali che $M_i \leq M_{i+1}$, e quindi non dobbiamo fare nessun ordinamento.

A questo punto utilizziamo il teorema del votante mediano, che ci dice che $M_2 = x_2$ è l'alternative che batte più alternative, e che quindi possiamo mettere come alternativa migliore nel ranking aggregato.
Togliamo $x_2$ dalle alternative, e calcoliamo nuovamente i vari peaks $M_1 = x_1, M_2 = x_3, M_3 = x_3$. Nuovamente, notiamo che i peaks sono già ordinati tale che $M_i \leq M_{i+1}$. Utilizzando il teorema del votante mediano concludiamo che $M_2 = x_3$ è l'alternativa che batte tutte le alternative rimanenti, e quindi che possiamo mettere in seconda posizione nel ranking aggregato.

Iterando questo ragionamento siamo in grado di costruire il ranking finale, che è il seguente

\[x_5 < x_4 < x_1 < x_3 < x_2\]