CNS - 02 - Semantic Security

Lecture Info

Date: [2020-09-23 mer 14:00]

In this lecture we have discussed an example of bad crypto in an RFID mutual authentication. We have then terminated the lecture by giving the rigorous definition of semantic security.

1 Encryption

Encryption is a security service who's goal is to protected the data confidentialty. This means that encryption alone only allows us to protect the contents of the message so that a possible opponent is not able to see and read it. Encryption alone doesn't protect the integrity of the data.

To do this we start from a plaintext $P$, and we transform it into a ciphertext $C$, which, hopefully, is incomprehensible. The message $C$ can then be transmitted over insecure channels, and the receiver can take it and transform it transform it back to the original plaintext $P$. Graphically,

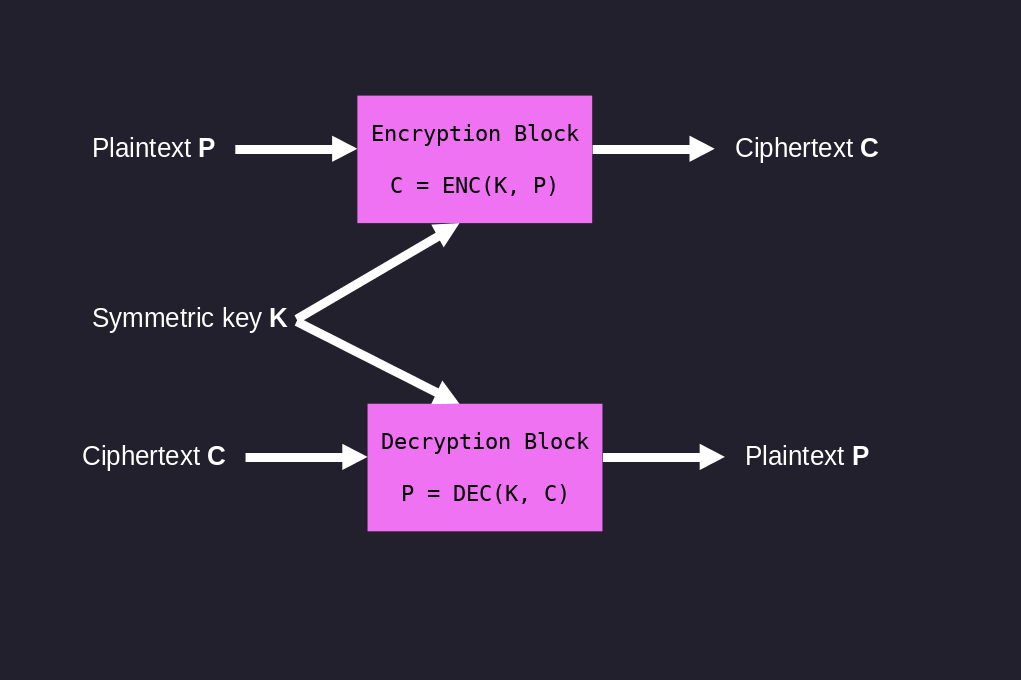
In the beginning we will only deal with symmetric encryption, which is characterized by the fact that the key to encrypt and the one decrypt are one and the same. There are also other form of encryption such as asymmetric encryption, where there are different keys involved in the encryption mechanism.

In general the encryption and decryption algorithm should be publicly known. The only secret part should be the key.

2 Substitution Ciphers

Let us now discuss a bad way to do encryption. Consider the following ciphered text

YCNWR CANWKR WL VCMY UQUMLIQ ICIIR RIIWYYRIR BRYYM URLW BMYYR URBSM. W
LMSW M JWQKRLWYW NRPMYYW, APRSIWIW AQPSR YR ESQLIM, NQL CLR FWRLNR M
AQIIWYM BWSWXXRICSR, AW SRKKQYJMKRL, BWMISQ WY NRPQ, WL NMSNOW
UQYIMPYWNW

BW ISMNNM, ISRPRAARIM BR YCLJOW APWYYW B'RSJMLIQ, VCRAW R JCWAR BM'
SRJJW B'CL'RCSMQYR. QYISM R VCMAIQ, NO'MSR Y'QSLRUMLIQ PRSIWNQYRSM BMY
JWQSLQ BMYYM LQXXM, YCNWR RKMKR VCMYYQ VCQIWBWRLQ B'CLR UQBMAIR

The ciphered text in this case was obtained by taking each letter of the original text and replacing it with another letter. Since the encryption must be reversible, if we mapped $A \to B$, then $C$ cannot be replaced with $B$, otherwise we would lose the property of reversibility. The mapping must therefore be a permutation of the alphabet of the original text. The key is the vector that tells me where $A$ goes, where $B$ goes, and so on.

2.1 Frequency Analysis

To actually break such cipher we can use various tools. One such tool is called frequency analysis.

We can for example to go the following site frequency analysis and we can count the frequency of each letter in the cipher text. The numbers obtained can then be compared with the frequency of letters in the italian language.

There are various relations of interest between the encrypted letters and the original ones which are revelead through the frequency. For example we can see that some letters repeat themselves. This means that these letters are probably associated to consontant.

This kind of procedure is called cryptanalysis, and it consists in trying to break a particular cipher in order to get the original plaintext from the cipher text without needing the encryption key. This type of attack in particular is known as ciphertext-only attack, which means that the only things we could use to break the cipher was the cipher text.

2.2 History Notes

Historically there have been various substitution ciphers, such as:

Ceaser cipher
Vigenere cipher

However viewed in mdoern light, they offer a really poor level of security.

2.3 Graphical Example

Consider the following picture

Let us now apply the substitution cipher to each pixel in the image. The resulting image is the following one

As we can see, even if the colors are a bit off, a lot of information can be gathered from looking at the ciphertext. Thus the substitution ciphers are really bad, and should be left to history.

3 Warm-up example 1: RFID Mutual Authentication

In a (real) scientific paper a technique to secure an RFID authentication system was proposed. The authors of the article proved the formal security of the system. Then, Bianchi, in 10 minutes, broke the system. In this lecture we will try to understand how the system was broken. This small example is not meant to teach anything in terms of technical knowledge, but rather it gives a big lesson in how you should look at this kind of systems to understand whether or not the crypto was wrongly used.

One critical issue of RFID is that they have to be implemented without using any batteries. This means that the mechanism must be extremely efficient and lightweight. Typically it works with a tag, which is like a card, and a reader, which is the apparatus which gives wireless power to the card and allows the communication between the card and the reader.

To work properly the tag must be authenticated, which means that at the beginning some authority has to give to each user a tag which has some sort of secret inside. This secret will later be used when trying to open the door. Even more. in some scenarios you don't want to limit yourself to prove the authenticity of the tag only. You also want to prove the authenticity of the readr, since otherwise a fake-door could copy the id of the tag. This other problem is called mutual authentication and requires that both parties prove to eachothers that they are authentic.

3.1 Wrong Solution

Consider the following basic solution: everytime we get to the door we communicate the secret S of the tag to the reader.

This is doubly wrong:

Since the communicatio is wireless, everyone can snoop in and know the secret S.
If the reader is fake, the reader can read the secret S.

3.2 Proposed Solution

The solution found was the following:

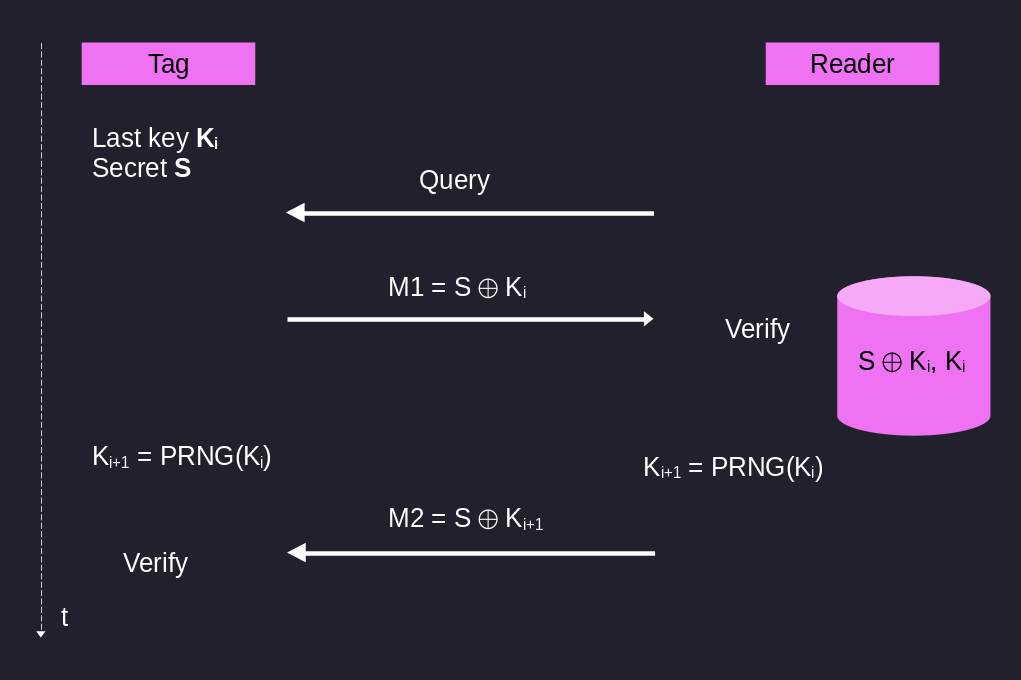
The tag stores two things, one static secret $S$ and a temporary value $K_i$.
Instead of transmitting to the reader the tag, when we get closer to the reader, the reader asks me to prove that I am a real user. To do so I transmit the following message

\[M_1 = S \mathbin{\oplus} K_{i}\]
The reader verifies using an internal database that the received XORed value is valid. Then, starting from the value $K_i$, the reader generates another pseudo-random value $K_{i+i} = PRNG(K_i)$ and transmits the message

\[M_2 = S \mathbin{\oplus} K_{i+1}\]
The tag then receives the XORed value from the reader, and by computing itself the $K_{i+1}$ it checks if the reader also knows the secret value $S$.
At the end of the exchange both parties store the value of $K_{i+1}$ so that the next exchange will be executed correctly.

Graphically we have the following

3.3 Does it work?

This scheme sort of makes sense because the secret is not transmitted in clear. To prove that the system was secure the authors of the proof used a formal analyzer called AVISPA. The system however is not actually secure. There is a way to break it. How do we break it then?

Consider the first message $M_1 = S\mathbin{\oplus} K_{i}$ sent by the tag to the reader. We know that $S$ is a random quantity,while $K_{i}$ is a pseudorandom quantity. The authors sold $M_1$ as properly enciphered using a vernam cipher. The crucial question to consider however is this: in $M_1$, who between $S$ and $K_i$ plays the role of the key, and who plays the role of the plaintext?

If the plaintext is $S$, then $K_i$ should be the key. But $K_i$ is pseudorandom, and not random. Therefore we break the assumptions required by the vernam cipher
If the plaintext is $K_i$, then the key is $S$, which means that between $M_1$ and $M_2$ we use the same key with different plaintexts. Once again, the assumption of the vernman cipher are broken, because the key repeats.

This means that the proof of security, which relied on the assumption that the messages were enciphered using a vernam cipher, is no longer valid, because the assumption are actually not true.

3.4 How to Break it

We will now understand how to break the system. Consider the following

\[\begin{split} M_1 \mathbin{\oplus} M_2 &= (S \mathbin{\oplus} K_{i}) \mathbin{\oplus} (S \mathbin{\oplus} K_{i+1}) \\ &= K_i \mathbin{\oplus} K_{i+1} \\ \end{split}\]

notice that both $K_i$ and $K_{i+1}$ are pseudorandom numbers. Also, $K_{i+1}$ is obtained by computing a function of $K_i$, that is $K_{i+1} = f(K_i)$. This means that we can sync up to the correct value of such quantitiy by simply iterating in a brute-force fashion over all possibilities. Since in the article $16$ bits were used to represent the $K_i$ values, we can run the following code

For(x_i = 0; x_i < 2^16; x_i ++) {
	Z_i = x_i \xor PRNG(x_i)
	if Z_i == M_1 \xor M_2 = K_i \xor K_{i+1}
	   break
}

Set K_i := PRNG(x_i)

Even if $64$ bits were used for the $K_i$ values this attack would've still been feasible.

Observation 1: This example shows the crucial difference between random and pseduorandom. Indeed, this attack only works because we can compute $K_{i+1}$ starting from $K_{i}$. If the $K_i$s were truly random, then we would not have been able to use this approach.

Observation 2: Can the system truly be improved? No, because to improve it we would require the $K_i$s to be truly random. In this case the scheme would not work anymore.

Observation 3: If the keys had more bits the system would become computational secure. It would still not be perfectly secure. In practice, as long as the key is below 64 bits the system would be easily broken. With current technology if the system used 128 bits it would have been a bit more secure.

3.5 Toy Example

Consider the following perfectly working pseudo random generator.

\[\begin{split} \text{prng}[0] &= 6 \\ \text{prng}[1] &= 3 \\ \text{prng}[2] &= 0 \\ \text{prng}[3] &= 4 \\ \text{prng}[4] &= 2 \\ \text{prng}[5] &= 1 \\ \text{prng}[6] &= 7 \\ \text{prng}[7] &= 5 \\ \end{split}\]

Suppose we are the attacker, and suppose we see the messages $M_1 = 5$ and $M_2 = 2$. To attack the system the attacker does the following

Starts by computing the XOR value of these two messages

\[M_1 \mathbin{\oplus} M_2 = 5 \mathbin{\oplus} 3 = 0101 \mathbin{\oplus} 0010 = 0111 = 7\]
Then, for $x \in \{0, 1, 2, 3, 4, 5, 6, 7\}$, we compute the values $x \mathbin{\oplus} \text{prng}[x]$ to get the following table

\[\begin{split} 0 \mathbin{\oplus} \text{prng}[0] &= 0 \mathbin{\oplus} 6 = 6 \\ 1 \mathbin{\oplus} \text{prng}[1] &= 0 \mathbin{\oplus} 3 = 2 \\ 2 \mathbin{\oplus} \text{prng}[2] &= 0 \mathbin{\oplus} 0 = 2 \\ 3 \mathbin{\oplus} \text{prng}[3] &= 0 \mathbin{\oplus} 4 = 7 \\ 4 \mathbin{\oplus} \text{prng}[4] &= 0 \mathbin{\oplus} 2 = 6 \\ 5 \mathbin{\oplus} \text{prng}[5] &= 0 \mathbin{\oplus} 1 = 4 \\ 6 \mathbin{\oplus} \text{prng}[6] &= 0 \mathbin{\oplus} 7 = 1 \\ 7 \mathbin{\oplus} \text{prng}[7] &= 0 \mathbin{\oplus} 5 = 2 \\ \end{split}\]
As soon as we reach the value 7, we know that $K_i$ = 3 and $K_{i+1} = 4$. This means that

\[S = M_1 \mathbin{\oplus} K_i = 5 \mathbin{\oplus} 3 = 6\]

Observation: If there are multiple values equal to the value $M_1 \mathbin{\oplus} M_2$, we will need more messages to break the system.

3.6 Conclusions

From this discussion we can infer the following things:

Whenever something is proved with a formal analyzer, it doesn't actually means that the system is truly secure. What it means is that, as long as the assumptions are valid, then the system is secure. If we make any mistake with our assumption however the security proof obtaind with such method is completely comprimised.
There is a huge, critical difference between random and pseudorandom.

4 How to Define Security

To give a proper, rigorous definition of security, let us try with some bad definition:

A cipher is secure when it protects confidentiality;
A secure cipher properly hides messages;
A secure cipher is one that cannot be broken;

These are "beautiful" definition that unfortunately do not anything (supercazzole, in italiano). Even the following definition, which seem better, do not satisfy all our needs

A secure cipher guarantess that every original byte is transformed into a different one.
A cipher is secure if the ciphertext is undistinguishable from a random string.

After years of a lack of rigorous definition of security, in the 1980s the cryptographic community came together and realize that "absolute" security hardly makes any sense. A better approach is to define security with respect to an adversary model.

Notice that a cipher may be secure against an attacker able to access only the ciphertext, but it might trivially be broken by an attacker able to see a few plaintext-ciphertext pairs. A choosen plaintext attack is an attack in which the attacker can see both the plaintext as well as the ciphertext.

4.1 Notational Convetion

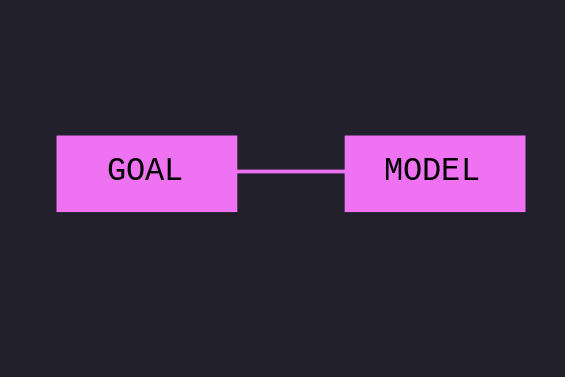
The notational convention is to define security according to the following scheme: we have a security goal and we have an adverserial model.

4.2 Semantic Security

The baseline requirement for any good cipher, also known as semantic security, is denoted as IND-CPA, which means

\[\text{INDistinguishability under Chosen Plaintex Attack}\]

4.2.1 Definition

To define such security we will construct a condition in which the attacker has a very favorable position. In particular we have our character (a girl) and an adversary. We then have the following

We only have two messages $M_0$, $M_1$ of equal size, which are choosen by the attacker;
The attacker sends the two messages to the girl;
The girl randomly picks one of the two $M_b$, where $b$ is a coin flip (random value in $\{0, 1\}$).
The girl sends back the message choosen encrypted with a key $K$ that only she knows. So the girl sends to the attacker the following value

\[C = \text{ENC}(K, M_b)\]
The attacker has also access to an oracle which has the same key as the girl and which lets the attacker encrypt any message he wants. So the attacker can send both $M_0$ and $M_1$ to the oracle to receive the encrypted version. This is the so-called choosen plaintext attack power.

We then say that an encryption system is semantically secure if, at this stage, the probability for the attacker to guess whether the message encrypted and sent by the girl is $M_0$ or $M_1$ is still $1/2$. That is, if I still have no information about what was inside $M_0$ and $M_1$.

When using this definition we can see that the verman cipher is semantically secure.

4.2.2 Technicalities

Technically speaking semantic security actually requires more things. The definition where the attacker has $1/2$ probability of distinguishing between the two messages is actually called perfect security. Semanting security then is a weaker version of perfect security, where the probability after you see many other messages is not strictly $1/2$, but rather that the difference of the probabilities is negligible and that it is computationaly unfesable to distinguish between the two messages.

While in theory this seems like a small difference, in practice this is a big difference, because it means that potentially a semantical secure system may still be broken with lots of data and processing power.

4.2.3 Consequences

Let us now explore the consequences of having a semantic secure system. In a semantic secure system an adversary must not be able to compute any information about a plaintext from its cipertext, even if it has access to an encryptio oracle (CPA attack). Saying it in another way, given two plaintexts of equal length and given a ciphertext which contains a randomly chosen message among these two, the adversary should NOT be able to distinguish which one i t is.

Some consequences of this are:

Encryption must be randomized:
- The same message, encrypted multiple times, must always encrypt to a different ciphertext.
- The ciphertext must be undistinguihsable from random.
If a substring repeats, it must encrypt to a different ciphertext.

By checking what kind of requirements is broken we can immediately understand whether or not the mechanim used is semantically secure.

CIAOCIAOCIAOCIAO -> f14dde57651b5cf7 (OK)
CIAOCIAOCIAOCIAO -> f14df14df14df14d (NOT OK)

4.2.4 Graphical example

Remember the Graphical Example showed before. If we take the same picture and we encipher each pixel with AES-128, a semantically secure encryption mechanism, we get the following

4.3 Uncoditional Security

The security of the vernam cipher is also known as perfect secrecy or uncoditional security. This comes from the fact that

\[\text{Information bit} \mathbin{\oplus} \text{random bit} = \text{random bit}\]

Indeed, consider a secret bit with probability $p$ of being $0$ and $1-p$ of being $1$, and a random bit with probability $1/2$ of being $0$ and probability $1/2$ of being $1$. Then we have the following

\[\begin{array}{c | c | c | c } \hline \text{Secret bit} & \text{Random bit} & \text{XOR Result bit} & \text {probability}\\ \hline 0 & 0 & 0 & \displaystyle{\frac{p}{2}} \\ \hline 0 & 1 & 1 & \displaystyle{\frac{p}{2}} \\ \hline 1 & 0 & 1 & \displaystyle{\frac{(1-p)}{2}} \\ \hline 1 & 1 & 0 & \displaystyle{\frac{(1-p)}{2}} \\ \end{array}\]

This means that the probability that the XORed bit is $0$ is $1/2$, while the probability that the XOred bit is $1$ is $1/2$. Thus, if we XOR a random bit with a secret bit, we will get a random bit. This is why the vernam cipher provides perfect secrecy.