CNS - 03 - Stream Ciphers (802.11 WEP)

Lecture Info

In this lecture we will introduce the concept of stream ciphers and we start the second example, showing how bad the 802.11 WEP protocol actually was.

1 Pratical Ciphers

In the previous lectures we have mentioned a bunch of time the vernam cipher. It must be understood however that such cipher is an idealization: it is not possible in the real world to have such cipher. When it comes to real-world, usable ciphers, they can be divided into the following classes:

2 Stream Ciphers

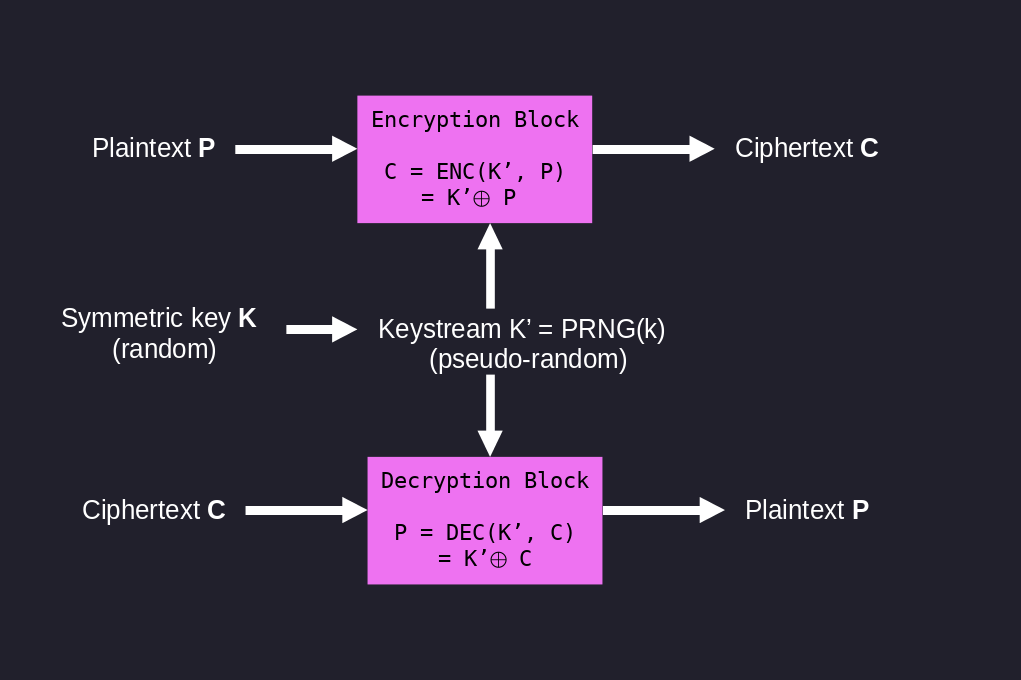
The goal of a stream cipher is to approximate a one-time-pad. The idea of a stream cipher is to use a private random key to generate a seed using a pseudo-random number generator. This seed is called a keystream to make clear that it is different from the key. Remember, the keystream is a pseudo-random value, while the key is an actual random value. The keystream is then XORed together with the plaintext to form the ciphertext.

Notice that the pseudo-random generator used by stream cipher is different from the ones we find in typical programming environments, like the rand() function offered by the C standard library. To summarise, the crucial difference between a one time pad and a stream cipher is that the first one uses a random key to encrypt the text, while the other uses a keystream to encrypt the text.

Observation: On the practice side of things when using stream ciphers, the fact that the key length is limited makes it more manageable to transmit it over a secure channel. Once the key is transmitted there's no need to re-transmit it.

The encryption and decryption operation uses the XOR operation in exactly the same way as the OTP (One-Time-Pad):

\[\begin{split} \text{CT} &= \text{ENC}(K, M) &= \text{M} \mathbin{\oplus} \text{keystream} &= \text{M} \mathbin{\oplus} \text{PRNG}(K)\\ \text{M} &= \text{DEC}(K, CT) &= \text{M} \mathbin{\oplus} \text{keystream} &= \text{CT} \mathbin{\oplus} \text{PRNG}(K)\\ \end{split}\]

Example: Consider the following example in which we want to encrypt the string "giuseppebianchi", assuming with a key \(k=1234567890\) we get

\[CT = \text{giuseppebianchi} \mathbin{\oplus} RC4(k) = \text{474d4caf78a844afa8b29add814e86}\]

With the scheme so far if in a single message a substring repeats, the ciphertext changes because the pseudo number random generator has a very long periodicty (of the order of \(2^{128}\)). This is a good thing. However, with only the scheme so far, if the same message is encrypted twice, the ciphertext will be the same, because the PRNG is deterministic, which means that given the same input (key \(K\)), it will give the same output (keystream \(K'\)). This means that our cipher is not semantically secure yet.

So how do we make our cipher semantically secure? To do so we'll introduce the concept of initialization vectors.

2.1 Initialization Vectors

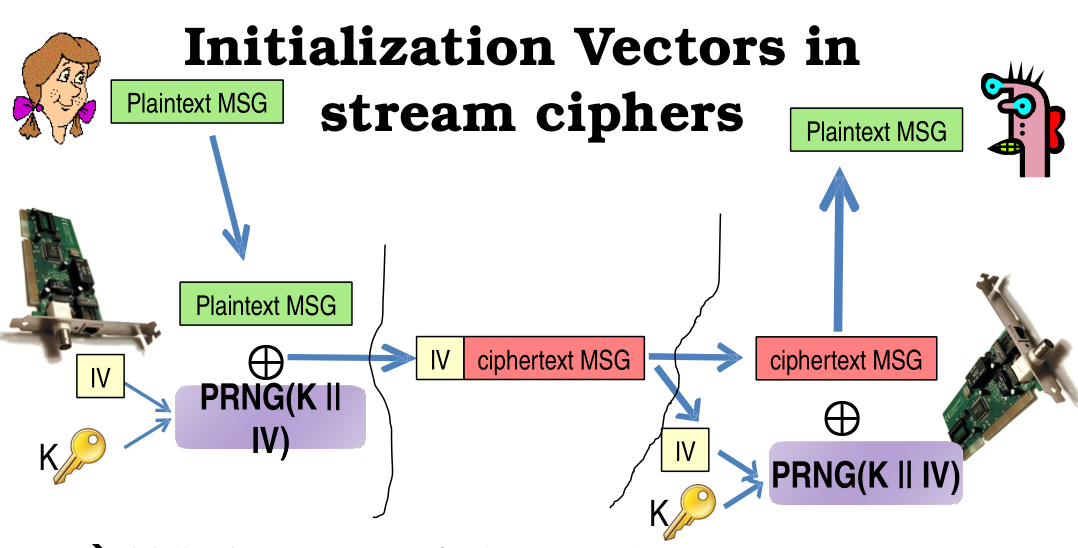
Suppose we have a plaintext message. This message will be sent to our transmission card, which is configured to transfer the message in a secure manner. The card therefore has to have stored somewhere the private key. Now, to make sure that by encrypting the same message we get a different output, when the card has to encrypt a new message, it will generate dynamically on the fly a vector of bits called an initialization vector (IV). The keystream is then obtained by using the PRNG() on the key juxtaposed with the IV, that is

\[\text{keystream} = \text{PRNG}(K \,\,|\,\, IV)\]

Using the keystream the plaintext is encrypted as always, but then, when we send the message, to enable the receiver to decrypt it, in the message along side the encrypted text we had the clear bits of the initialization vector.

Note well: If a stream cipher is good, it should not be possible to get the key if the attacker knows the initialization vector used to generate the keystream which encrypted the emssage.

Observation: The difficult part of stream cipher is the \(\text{PRNG}()\) used to generate the keystream starting from the key and the initialization vector.

It can be proved that this system is semantically secure if the IV will never repeat.

3 The Dunning-Kruger Effect

As we already saw in the warm-up example \(1\), good crypto can be badly used. Indeed, most breaches exploit poor protocol constructions and vulnerabilities. This, as we will see in this lecture and the next one, is exactly what happened with the 802.11 WEP protocol.

Before starting to analyze what mistakes were made however its important to know the following fact of life: If you don't know a topic, you believe you are an expert, when you know a topic, you understand what you are not. So, the less you know, the more you think you are good.

This effect was studied in a paper named *Unskilled and Unaware of It: How Difficulties in Recognizing One's Own Incompetence Lead to Inflated Self-Assessments* done by Dunning and Kruger. Their work can be roughly represented with the following graph

The interesting effect that the more you know, the less you think you know and the less you're prone to define yourself as an "expert".

4 Warm-Up Example 2: 802.11 WEP (part 1)

The Dunning-Kruger effect is exactly what happened with the guys who designed WEP (Wired Equivalent Privacy), which is the first generation of wifi security.

The WEP guys were the the ones who designed the wifi protocol in the 1997-1999. They did not have crypto-specific knowledge, but instead they thought that by simply using good ciphers they could manage to offer a baseline level of security without too many problems. In particular WEP had three goals:

This result is actually quite embarassing, because the WEP guys were not students, but they were a group of standardizers. For this reason the WEP example is extremely important to keep in mind, because it is a real world example of how to make things incredibly wrong.

4.1 WEP Cipher: RC4

RC4 is a specific PRNG algorithm used to generate the keystream starting from the key. Today it is considered weak, but at the time it was considered to be strong.

Even though the cipher used, CR4, is broken, its crucial to understand that the mistakes made in WEP were at the level of the protocol, not at the level of the crypto. So even with a strong cipher, the system would've still be broken.

The idea of RC4 encryption is the same as the general stream cipher we've seen before. The only thing that changes is the PRNG used

\[\text{ENC}(k, m) = m \mathbin{\oplus} \text{RC4}(\text{IV}, k)\]

4.2 WEP and IV

In WEP every single packet must have a different initialization vectors. This comes from the fact that in WiFi connections packets might never arrive at the destination, and therefore its a big problem to keep the stream syncronizhed on both ends. To solve this problem you need to generate an IV for every new packet.

If we assume RC4 strong, then WEP is secure as long as IV never repeats. In other words, we have the same keystream iff we have the same (Key, IV). Since typically we assume the Key to be static, then we must have IV to change everytime. Indeed, suppose the IV repeats, then we have

\[(m_1 \mathbin{\oplus} ks_i) \mathbin{\oplus} (m_2 \mathbin{\oplus} ks_i) = m_1 \mathbin{\oplus} m_2\]

and thus if we know one message we can get the other one, thus we lose our semantic security. Also, if the IV repeats, the weakness is practical to exploit, because it is easy to create a KPA (Known-Plaintext-Attack) or a (Choosen-Plaintext-Attack, stronger than known) condition in wifi.

Even if we don't know the content of any of the two messages, since the messages are not random and therefore have limited entropy, we can infer the contents of the messages.

We know so far that the IV is crucial to ensure the security of the system. This knowledge is not that widespread, and it can happen that good programmers who know not much about crypto put values like \(0000\) or \(1111\) as the IV value, which obviously totally breaks the system.

Now, WEP didn't do this, but instead they made two mistakes:

  1. They choose \(24\) bits as the size of the IV. Notice this is a mistake: you want the IV to be long, because you don't want it to repeat itself, so the longer the better.

  2. They did not enforce any mechanism for the generations of the IV, but instead they left this task to the implementors. This meant that any vendor and any programmer with no security awareness could write any mechanism to generate such values.

4.2.1 Repeating IV in WEP

If a cyclic generation of IV is used, then with 24 bit we can generate \(2^24\) vectors. Notice that this in wifi is not much: assuming \(1500\) bytes frames with \(7\) mbsp (net) wifi throughput, then IVs recycle after less than 8 hours. This means that an attacker after \(8\) hours I have all the possible initialization vectors that could possibly be used.

If you generate the IV randomly, then by the birthday paradox (which we'll cover in a future lecture), then we have a 50% collision probability after approximately \(2^12 = 4000\) frames.

When you think critically about these things a lot of issues are encountered. For example, what do you do after a reboot with respect to the IVs? In many cases devices simply restart their IV sequence from the start. This however would only help the attacker.

4.2.2 Pratical Attacks to Small IV Space

The idea is to create a dictionary that maps initialization vectors to relative keystream.

\[\text{IV} \to \text{RC4}(\text{IV}, \text{Key})\]

Then, once we have built or dicionary, whenever we see a new message that comes with a specific IV, we can simply use the associated keystream to decrypt the message. All of this does not require the attacker to know the key.

Question: Is it necessary to store all of the IVs in our dictionary?

Answer: Yes it is, because as long as we miss an IV entry, if the cipher used is good, then we should not be able to guess it using the other entries of our dictionary. Each entry should be independent of the others. A good crypto is completely resistent to any interpolation or things of the sort.

Another way to attack the system is to wait for the IV to repeat.

In the original WEP the key was \(40\) bits long. Then the original implementors defined a new version of WEP with a \(128\) bit. This "improvement" however was only partial, superficial and didn't solve the actual issue: the IV in both versions was only \(24\) bits long.

4.3 FMR Attack

Fluhrer, Mantin and Shamir showed a weakness inn RC4. They showed that some weak IVs leaked information of the key into the keystream. With a 5% probability, a byte in the keystream is equal to a byte in the key. Notice that this is a much stronger weakness, because it allows you to get the key.

Then, Stubbflefield, Ioannidis and Rubin used and exploited that weakness and found a linear time attack with respect to the key size. This attack exploited the fact that in WEP the payload some bytes of the encrypted payload are always costant and do not change. This gives the attacker much more power and makes the attack much more faster.

4.4 Lessons to Learn

WEP teaches us two things to never, ever do:

  1. Never, ever, use few bits for the initalization vectors.

  2. Never, ever, leave the implementation of the IV generation to the vendors and future implementors. When you do a security audit, research and understand how the IVs are being generated.