CNS - 06 - User Authentication I
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: CNS 06 - User Authentication
Introduction: In the last lecture we discussed the difference between passwords and secrets. From now on we will treat passwords and secrets as the same thing (even though they are different in practice!), that is, they both allows me to authenticate. In this lecture we will talk about protocols used to authenticate.
1 User Authentication
Authentication is a proof of knowledge process in which we have to prove that we know the password. Notice that proving we know the password does not necessarily imply we have to show the password, although showing the password is sufficient to prove that we know the password.
There are also different techniques which can be classified by how much they reveal, such as
PAP, Full disclosure
CHAP, Some information leaks
ZKP, no information leakeages (zero-knowledge protocols)
Modern cryptography makes use of zero-knowledge protocols, which have no information leakage, that is, they reaveal nothing. These methods however are typically more complex to implement, and so in real systems we dont see much of them. For example in 4/5G CHAP protocols are used.
Remember that
One-way authentication: user proves to the site he is authentic.
Mutual authentication: both parties provide to eachother their authenticity.
2 PAP
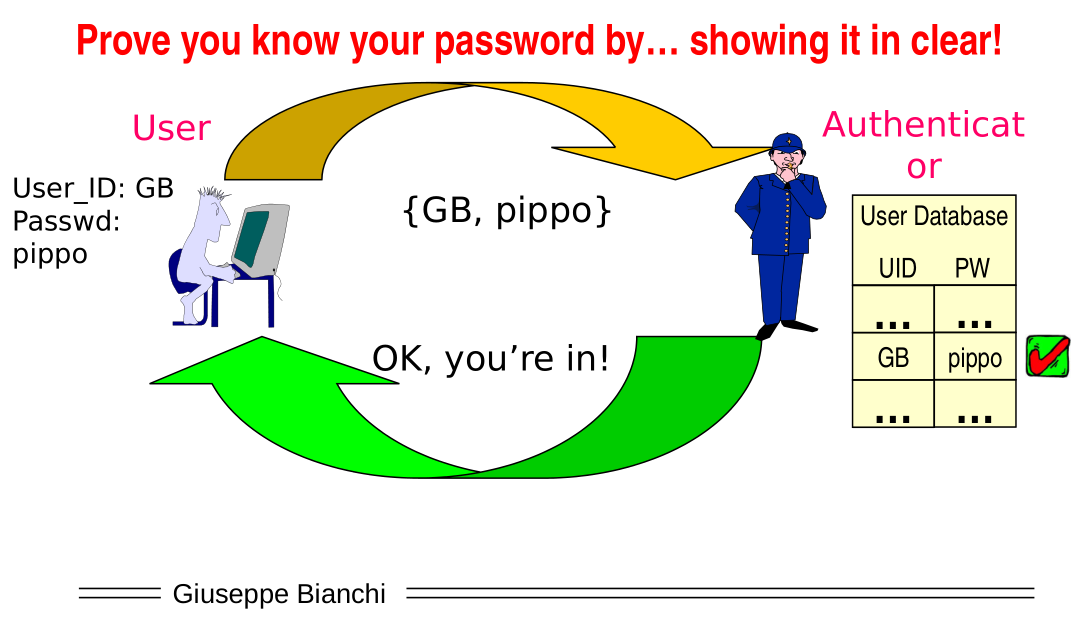
PAP (Password Authentication Protocol) is the simplest possible authentication approach.
In PAP the password (the secret) is pre-shared between the user and the authenticator. When the user wants to authenticate, he simply shows the password in clear to the authenticator. The authenticator has a big database, which is looked into when the user passes to it his password. If the check works out fine, that if the password sent by the user is found within the db, the user is authenticated.
2.1 Pros and Cons
That this protocol is used a lot (for example in the delphi
platform). Being extremely simple, this protocol has many
limitations:
The password is sent in clear, which means that if the channel permits eavesdropping (that is, ability to listen what is transmitted, typically of wireless networks), then its game over.
This means that PAP does not permit mutual authentication with a single secret, because in the first round you reveal the actual password. To do mutual authentication you would need two secrets, one per party.
NOTE WELL: Using the wifi campus, if you don't use TLS your connection to the AP can be seen in clear.
No protection from replay attacks. In a replay attack an attacker graps a message from a channel only to then retransmit the message previously grabbed over the channel to authenticate himself.
With PAP an attacker does not even need a "true" replay attack, since by seeing the message he already sees the password in clear.
No protection from repeated authentication attempts.
2.2 Example of PAP (PPP trace)
Consider sniffing the following PPP trace sent during an authentication process which used the PAP protocol.

Since the contents are all sent in clear, to actually get the uid and the password you simply need to understand the structure of a PPP packet

As we can see, both the UID as well as the password are sent in clear.
3 CHAP
CHAP - Challenge Handshake Authentication Protocol
The idea is to prove that I know the password without actually revealing it explicitly. To do this we introduce the concept of proof of knowledge, which is the result of a computation that can only be done if we know the secret.
If \(p\) is the secret, I am not telling you \(p\), but I'm telling you \(f(p)\), and I'm able to compute \(f(p)\) only because I know \(p\). To make this mechanism robust, the function \(f(\cdot)\) has to have some properties. For example, \(f(\cdot)\) cannot be the square function \(f(x) = x^2\), because the square function can be easily reversed. The properties desired are thus the following:
Not Reversability: The computation must NOT reveal the secret itself. If \(r = f(p)\), then the inverse \(p = f^{-1}(r)\) must NOT be computable. That is, we cannot invert the function.
Not Replayability: \(f(p)\) must not be replayed by an attacker. This means that \(f(p)\) cannot be a function only of \(p\), but it must include a nonce (also called a challenge).
The protocol is described as follows
The authenticator sends a challenge to the remote user. The authenticator also has to make sure that the challenge never repeats.
The remote users computes the reply
\[R = H(\text{Challenge}, \text{Password}, \text{etc...})\]
and sends to the authenticator the \(\text{UID}\) and the computed reply \(\text{R}\).
The authenticator takes the \(\text{UID}\) sent by the user and uses it to retrieve the password from the local db. After that he applies the function \(H\) with the challenge sent and computes again, separetly from the user, the value
\[X = H(\text{Challenge}, \text{Password}, \text{etc...})\]
After that he compares the result he himself obtained \((X)\) with the result sent by the remote user \((R)\) The final result of the authentication comes down to the result of this comparion: if both strings are the same, the user is authenticated, otherwise the user is not.
Graphically we get
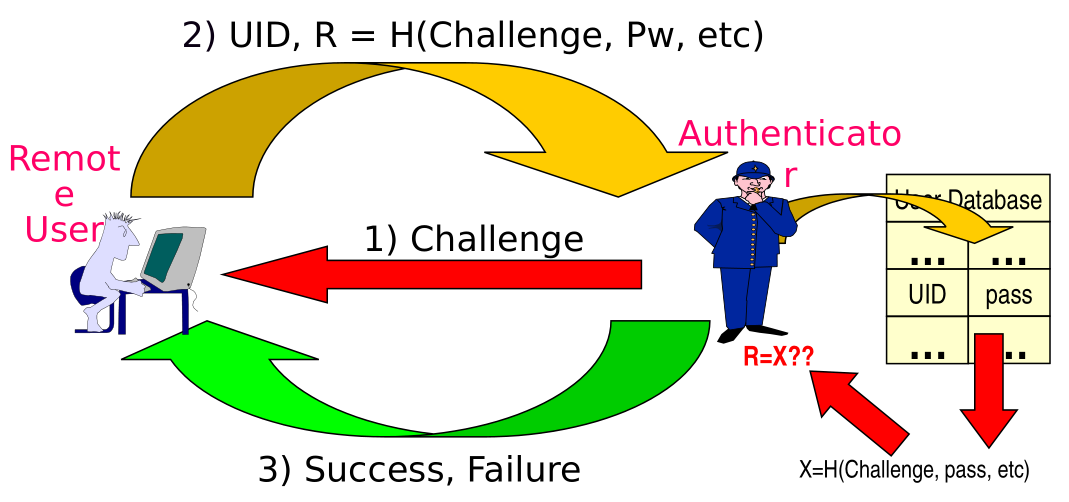
Notice in the scheme how the authenticator does not need to reverse the function, he can simply re-computed the function \(H(\cdot)\), since he has all the inputs of the function.
3.1 Pros and Cons
Pros of CHAP:
Protection against replay attacks.
Initiated by the Authenticator.
Repeated Challenge. Authentication may be repeated over connection time. Authenticator controls the frequency and timing of the challenges. This is good, as it limits the time of exposure to any single attack.
Cons of CHAP:
Secrets must be avaialble in plaintext form. We cannot use irreversibly encrypted password database, because the authenticator has to compute the proper value of \(H(\cdot)\).
The only cons of CHAP is pretty critical and we will discuss more about this on monday.
4 Hash Functions
Intuitively an hash function can be imagined as a "tritacarne", because it takes something as a input (some meat) and it scrambles it to give you a something which is uniquely associated with that input (a sort of fingerpint).

Conceptually an hash function (even non crypto) is a "summary function" that takes an arbitrary message of length \(X\) and gives as a result fixed size value \(Y = H(X)\) that we call digest (digest is the name assigned to the result of an hash function).
\[\text{arbitrary size } X \to \text{ fixed size } Y = H(X)\]
Generally an hash function should be relatively easy to compute for any given X. The minimal level of security for today standards is SHA256 which has a digest of the size of \(256\) bits. Older hash functions like MD5 are broken and should not be used.
Notice that the input can be shorted than the fixed size. To give some example, you can use the sha256-hash-calculator site to compute some SHA-256
(string) giuseppe is going to the see (sha-256) 4a6e0e11ccaa265d61e8239d31f5e2c47fd93876343617db84ad37a22b86e368
4.1 Non-Crypto Hash Functions
Not all hash functions are cryptographic. We will now see a couple of toy examples which are NOT hash function.
4-bit parity vector (toy example of checksum): Remember that a parity bit is a bit that is \(1\) if the number of 1s in the code is odd, and \(0\) if the number of 1s in the code is even.
A 4-bit parity vector is computed by splitting the code into blocks of \(4\), and using the first column of each block to compute the first parity bit, the second column to compute the second parity bit, and so on until the fourth parity bit. For example, conside the sequence
\[X: 0110 \;\; 0011 \;\; 0111 \;\; 0010 \;\; 0100 \;\; 0010\]
Then its parity vector is \(H(X): 0110\). Notice that this is an hash function, because the message can have arbitrary size, but the final output (the digest), has a fixed size of length \(4\), which is known, and which does not depend on the input. Notice also that the function is not invertible, because multiple different messages hashes to the same result.
Modular checksum: Split a message into chunks, and sum the various chunks with a given modulo \(1000\)

Call Center control (Human Computable hash): When you call a call center, you need to give it your password. Since the people in the call center cannot know the entire code, what happens is that they ask you for example the 2nd or the 5th digit of your passcode. In general they ask you some digits of your password.

Notice that any hash, irrespective of strength (crypto or not), is always NOT invertible, because its inputs are way more than its outputs, and therefore it must map more than one input to a given output.
4.2 Crypto Hash Functions
What we require for cryptographic hash functions is a property that we call ONE WAY, which is different from simply invertibility. Informally speaking a cryptographic hash function should have the following properties:
It takes an input of arbtirary size and squeezes the input to a fixed size (like any other normal hash functions).
If we change a bit of the original text the final result of hashing should look to be completely independent with the hash of the original text.
It should look like a radom message and in general it should try to approximate as much as possible the generation of a random message, even though it cannot really be random (because its generated with a function, and is thus deterministically determined by the input).
It should make it impossible for an attacker to either create or purposedely modify/extend/replace initial text.

More formally, a cryptographic hash function should have the following properties:
Preimage resistance (one way):
Given \(Y\), it is (computationally) hard to find any \(X\) such that \(H(X) = Y\).
Second preimage resistance (weak collision resistance):
Given \(X\), it is hard to find another \(X'\) such that \(H(X) = H(X')\).
Collision resistance:
Hard to find two generic \(X_1\) and \(X_2\) such that \(H(X1) = H(X2)\).
Let us now discuss more in depth each one of them.
4.2.1 Preimage Resistance
Given \(Y\) the result of a hash (the digest), it must be HARD (computationally speaking) to find any \(X\) such that \(H(X) = Y\).
This property way is much stronger than "non-invertible". Indeed, in theory there are an infinite number of \(X\) which give \(Y\) as a result. However when using crpyto hash, finding these values of \(X\) must take years and years and be computational impractical.
Exercise: Prove that none of the previous toys example are one-way.
A corollary of this property is that, in order to be one way, the size of the digest must be large enough. Indeed, suppose that you design an hash with a fixed digest of only \(4\) bits. With this low size as a digest, I can simply brute-force by trying lots of different messages and find a message with a specific digest. Because even if the hashing is well done, the result of the hash \(H(X)\) should approximate a random generated message of 4 bits. This means that the probability of getting a particular message is \(1/16\), which means that in average with \(16\) tries I can find the specific message I am looking for.
This means that a possible attack to an hash function is thus to try multiple inputs until you find a particular digest. This is exactly how bitcoin mining works: each miner tries to find an input \(X\) with a specific digest.
Obviously though a large digest is NOT ENOUGH to have a good crypto hash, because, for example, MD5 has a 128 bit digest, but the hash function itself was broken. SHA-1 has 160 bit digest, but as of today can be broken with about 2^61 attempts (pratical with cloud resources).
4.2.2 Second Preimage Resistance
Given \(X\), it is hard to find another \(X'\) such that \(H(X) = H(X')\). As an attacker, it should be hard to find another message that hashes to the same hash.
Notice that this property is stronger than simple one-wayness. Indeed, there are function that are one-way but still fail this property.
Example: To guarantee that the technician does not change something inside an hard drive which is used in a juridical process by a judge, the judge computes the hash of the entire disk, and if you are the analyst and you change something, then the hash will be different.
In practice some analyst still use MD5, which is broken and so give no guaranteees.
Extra: Nelle reti 4/5G il protocollo CHAP è seguito da un key agreement. Questo permette di evitare attacchi di tipo Session-Hijacking. I protocolli *AKA ti difendono alla session-hijacking, in quanto oltre all'autenticazione viene generata una chiave di cifratura che non può essere generata da terzi parti.