CNS - 07 - User Authentication II
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: CNS 06 - User Authentication
Introduction: In this lecture introduced the last property that an hash function should have and we have compared the difference between the PAP and CHAP protocols.
1 Hash Functions
We ended the previous lecture by discussing cryptographic hash functions. Let us now remember the three properties that a hash function has to have in order to be a cryptographic hash function:
Preimage resistance (one way):
Given \(Y\), it is hard to find any \(X\) such that \(H(X) = Y\).
Second preimage resistance:
Given \(X\), it is hard to find another \(X'\) such that \(H(X) = H(X')\).
Collision resistance:
Hard to find two generic \(X_1\) and \(X_2\) such that \(H(X1) = H(X2)\).
1.1 Example: Discrete Logarithm
Let us now see a function that has the first property (preimage resistance) but not the second (weak collision reistance). The function is defined as follows
\[Y = F(x) := g^x \mod p\]
where \(g\) is a known value and \(p\) is a very large prime.
Notice that \(F(x)\) is a one-way function, that is, it satisfies the first property. Indeed, even though the exponential function \(3^x\) is trivially invertible in ordinary arithmetic (\(x = \log_3 3^x\)), when working with modular exponentiation, this problem becomes very hard to solve efficiently if the values for \(g\) and \(p\) are carefully choosen.
In general, when we are working with a function that is somewhat regular (monotone, for exmaple), then it is always possible to invert the function, since even in the cases where an analytical formula is not available, we can always use numerical techniques to find our inverse. When instead the function is not regular but looks like random, then it usually is hard to invert. If we plot the funciton \(F(x)\) with parameters \(g=2\) and \(p=101\) for different values of \(x\) we find the following
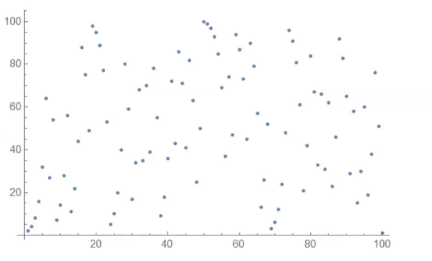
The function \(F(x)\) is called the discrete logarithm and its a really important function to cryptography. The problem of computing the value of the discrete logarithm when \(p\) is a very large prime its considered to be a computationally hard problem to solve.
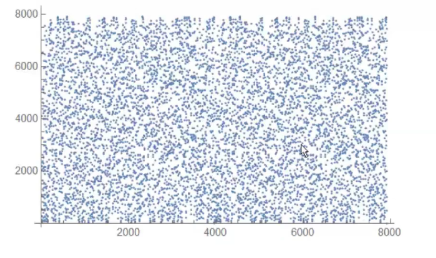
Notice that while given a value \(y\) it is hard to find an \(x\) such that \(F(x) = y\), if we found an \(x\) such that \(F(x) = y\) we can compute an infinite numbers of \(X'\) such that \(F(x') = y\) since we can simply define
\[x' := x + (p-1) \cdot k\]
and notice that \(F(x') = y\) for any value of \(k\).
Observation: Don't think that its easy to find a cryptographic function. MD5 was broken in 2005 because they found out some internal mechanism to find a collision, such that they were able to construct a different message having the same hash.
1.2 Strong Collision Resistance
In the third property we ask that you should not find any pair of messages that have the same hash. This add a degree of freedom with respect to the second property, which means that the third property is stronger than the second one. So there will be functions that satisfy the first two conditions but not the third one.
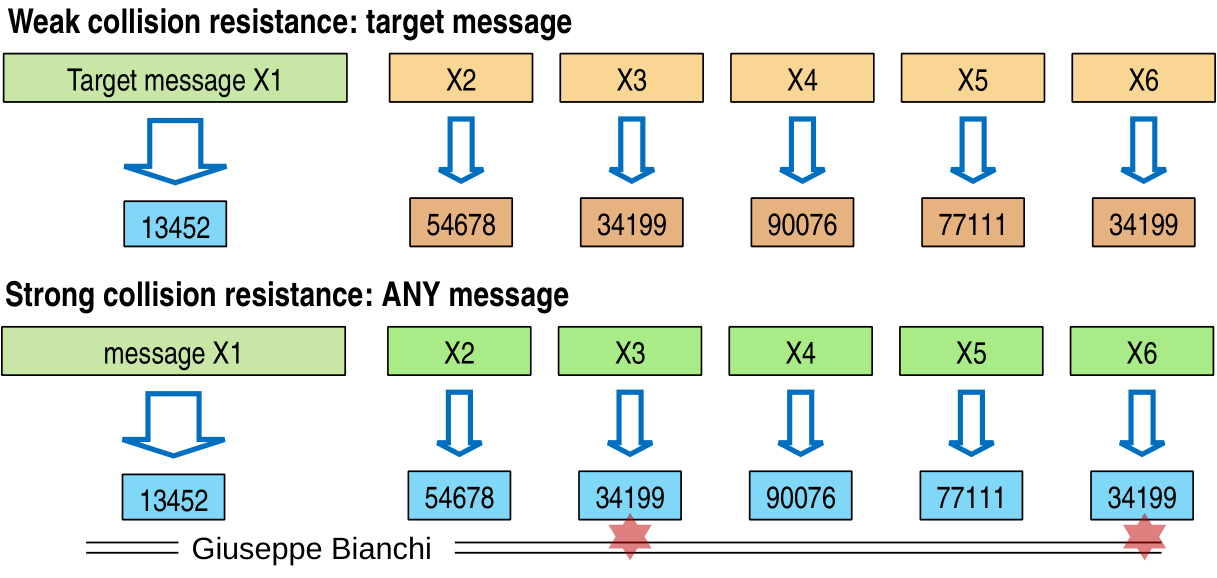
1.2.1 The Birthday Paradox
As a direct consequence this property sets a minimum size for the digest because of the so called birthday paradox. To understand this paradox let us define as an hash function of a human being the day and month of their birthday. For example,
\[H(\text{giuseppe bianchi}) = 1012\]
Consider now a class of \(k=23\) people.
What is the probability that none of the remaining people \(k-1 = 22\) were born in the same day as giuseppe bianchi?
\[\Big(1 - \frac{1}{365} \Big)^{22} = \Big(\frac{364}{365}\Big)^{22} = 94.1\%\]
What is the probabilit that no two people of the \(k=23\) were born in the same day?
\[\begin{split} 1 \cdot \Big(1 - \frac{1}{365} \Big) \cdot \Big(1 - \frac{2}{365} \Big) \ldots \Big(1 - \frac{22}{365} \Big) &= \frac{365 \cdot (365 - 1) \ldots (365 - 22)}{365^{23}} \\ &= \frac{\frac{365!}{(365-23)!}}{365^{23}} \\ &= 49.3\%\\ \end{split}\]
\[\]
Experiment: During the lecture we took the following data
1012 1001 1207 1810 3011 0211 1111 1701 0610 0304 1603 1301 1802 1511 0107 2204 0305 0503 3012 2705 1208 2901 3011 0506 0805 0808 1710 1104 0402 0610 0605 1803 3107 1608
As we can see, we have two collisions (3011 and 0610).
So, the takeway here is that it is not surprising to find two people in a classroom having the same property, since that is highly probably, especially when you have a class with lots of people. What is surprising is actually is finding someone with your own birthday, since that would be aking of satisfying the 2nd property, which is the weak version of collision resistance.
1.2.2 Why digest size matters
Let us now be more general and study the consequences of this birthday paradox with respect to the size of the digest.
Let \(n\) be the number of bits in the digest. The actual number of digests is then \(N = 2^n\). Let \(k\) be the number of messages, and let \(p\) the probability of collision in the \(k\) messages. The probability of not having collisions in \(k\) messages can be computed as follows
\[\begin{split} P(\text{no collision}) &= 1 - p = \frac{N!/(N-k)!}{N^k} \\ &= \frac{N}{N} \cdot \frac{N-1}{N} \cdot \frac{N-2}{N} \ldots \frac{N - (k-1)}{N} \\ &= 1 \cdot \Big(1 - \frac{1}{N}\Big) \cdot \Big(1 - \frac{2}{N}\Big) \ldots \Big(1 - \frac{k-1}{N}\Big) \\ &= \prod\limits_{i = 1}^{k-1} \Big( 1 - \frac{i}{N} \Big) \\ \end{split}\]
Consider now the fact that \(N\) is usually a large nubmer, where \(k\) (and thus \(i\)) is a small number if compared to \(N\). But then then \(x:= i/N\) is small, and we know from analysis that when \(x\) is small we can approximate \(1 - x\) with \(e^{-x}\). We thus get the following
\[P(\text{no collision}) = \prod\limits_{i = 1}^{k-1} \Big( 1 - \frac{i}{N} \Big) \approx \prod\limits_{i=1}^{k-1} e^{-i/N} = e^{\displaystyle{-\frac{\sum\limits_{i=1}^{k-1} i}{N}}}\]
Finally, since we know that \(\sum\limits_{i = 1}^{k-1} i = k(k-1)/2\) we get
\[P(\text{no collision}) = 1 - p \approx e^{\displaystyle{-\frac{\sum\limits_{i=1}^{k-1} i}{N}}} \approx e^{\displaystyle{-\frac{k^2}{2N}}}\]
We can know directly obtain \(k\) by inverting the function, to obtain
\[k = \sqrt{2N} \cdot \sqrt{\log{\frac{1}{1-p}}}\]
since we are interested in finding out when we have a \(50\%\) chance of collision, the number of messages we need to collect to have a \(50\%\) to collide is
\[k \approx \sqrt{2} \cdot \sqrt{\log2} \sqrt{N} \approx 1.777 \sqrt{N}\]
This means that if we use a digest of \(N=2^n\) bits, we have a \(50\%\) chance of having a collision if we collect as little as \(2^{n/2}\) number of messages.
The takeway here is that the hash size must be assessed against birthday paradox. The following examples show how this is done:
Suppose that RAND with 32 bits is a random function with \(2^32 = 4.3\) billion outputs. We have \(50\%\) collision after \(2^16 ~ 60.000\) msg (very little).
Take DES, which is a block cipher with \(56\) bits. We have a \(50\%\) collision probability after \(2^28 ~ 250.000.000\) messages.
Take MD5, which has a digest size of 128 bits. We have a \(50\%\) collision after \(2^64 = 1.8 \times 10^19\) (weakish today). Notice that MD5 is broken because they find out other issues that leads to collision.
Take SHA256 with a digest size of 256 bit. We have a \(50\%\) collision after \(2^128 = 3.4 \times 10^38\), which is ok by today standards.
Summary: The conclusion is that the security level of a \(n\) bit digest is NOT \(2^n\) but rather \(2^{n/2}\).
1.3 Assesing security (is Hard)
Assessing the security of a system is hard, because proving security is usually done by starting out with some assumption, since proving things mathematical is just way too hard.
In proving part of the security of AES they used some group theory. But in general its very rare. For example the security RSA system is obtained by assuming that factoring numbers is hard. In the quantum computing world there is the schnorr algorithm, which factorizes numbers in a linear complexity.
2 PAP vs CHAP
Let's now go back to the discussion of user authentication. In the previous lecture we defined the two protocols: PAP and CHAP. In CHAP usually an hash function is used to generate the challenge. Let us now compare these two protocols.
When we talk about security its crucial to clarify what is the adversary model. Only a beginner would say something like "system is sufficiently secure". The typically attack models are:
Attack the communication channel: eavsdropping, MITM, replay.
Attack to the backend UID-passwd database: attacker penetrates system and steals entire password DB.
2.1 Hashed Password in PAP
Against the second attack, the one on the DB, PAP is way better than CHAP. Because in PAP we can do some mitigation on the security of the database by protecting the password.
The basic idea is that instead of storing the plaintext password, the authenticator stores the hashed version of the password, so that in case of an internal breach, the only way to break the db is to brute force it or use a dictionary attack. The protocol also does not change with respec to the user: the only thing that changes is that now the authenticator has to compute the hash of the password everytime a user wants to log in.
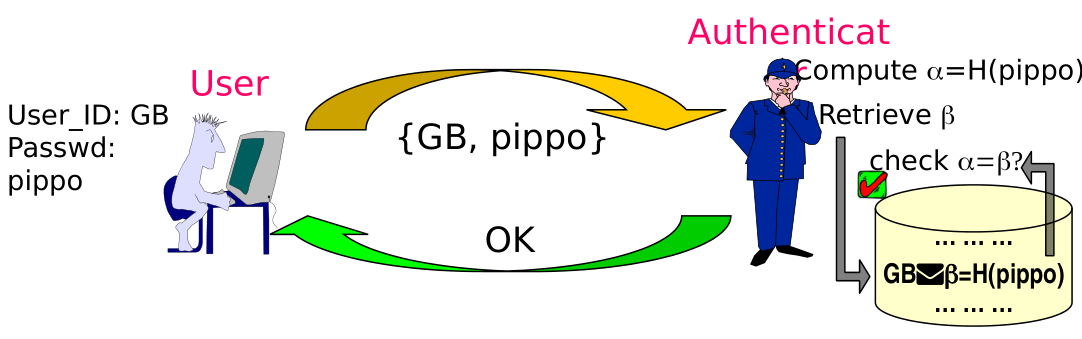
With this approach security ultimately depends on choosing a "strong" password with a high entropy value.
2.2 What about CHAP?
Notice that in CHAP we cannot hash passwods, since the challenge is replied by computing the hash \(H(\text{challenge}, \text{password})\), and the challenge changes everytime.
In the backend side, in order to compute the same value we would thus need both inputs. Even if we stored the \(H(P)\) on the database, then the \(H(P)\) becomes essentially the new password, and thus an attacker that attacked the DB could simply use \(H(P)\) instead of \(P\).
In CHAP there is simply no way to protect the password database.
2.3 Conclusions
In general then if we have a secure communication channel then PAP is better than CHAP, while if we don't have a secure communication channel but we have a secured backend infrastructure then CHAP is better than PAP.
There is no single solution, it all depends on the specific threat you want to protect yourself from. Having said that, at the end of the day most platform use a PAP authentication protocol over an SSL/TLS tunnel, which is created for protecting the communication channel before sending the data.
2.4 CHAP with Salt
CHAP was modified by adding some "salt". In this modification initially the authenticator sends two things: a challenge value, as always, and a salt value. The response from the user is then computed as follows
\[\text{Response} = H(H(\text{salt}, \text{password}) \;\;|\;\;\text{challenge})\]
I can then create a database in which I store in the database all the hash of the password with the salt. In this way the db depends on the specific salt value, which means that if the db gets stolen, then we can throw the DB out of the window and we can create a new one with a different SALT. To do this however you still need another database in which you have the password stored in clear.