CNS - 08 - User Authentication III
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: CNS 08 - User Authentication
Introduction: Today we will introduce a couple of extra details on PAP/CHAP authentication.
1 One-Time Password
How can we extend a password authentication protocol so that we can have a different password at every attempt? This modification would prevent replay/playback types of attacks.
At first glance this looks trivial: simply create a db with a list of pre-generated passwords. Even though this is trivially possible to implement, this solution is terrible in terms of real world scaling. We thus need more scalable solutions.
1.1 Hash Chains
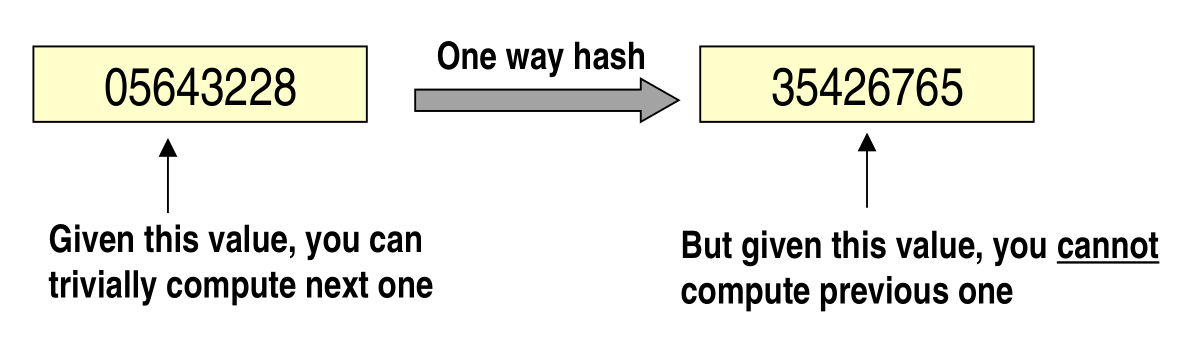
A better idea is to use hash chains. An hash chain is obtained by starting from a single seed value and using a cryptographic hash function to obtain the next value of the chain. Since we're using a crypto hash, the key characteristic of hash chains is that, given a value of the hash chain, you cannot compute the previous value in the chain, but only the next one.
Formally we have
\[\begin{cases} P[0] &= \text{seed value} \\ P[1] &= H(P[0]) \\ \;\;&\vdots \\ P[i] &= H(P[i-1]) \\ \;\;&\vdots \\ P[N] &= H(P[N-1]) = \text{last value} \\ \end{cases}\]
To actually use this chain let us discuss what the user should do and what the authenticator should do.
The user has to compute the values \(P[i]\) of the chain until the last value \(P[N]\). Once that is done the user can start using the passwords in reverse order, starting from \(P[N]\), then using \(P[N-1]\), and so on until we reach the seed value \(P[0]\). With this order an attacker cannot generate the next password, since that would require inverting the hash, which is not computationally feasible.
The authenticator instead cannot simply save the seed value \(P[0]\), for otherwise to check if \(P[n]\) is valid he would've to do \(N\) hash computation, which is unfeasible the moment you think that the authenticator has lots of clients. A better approach is the following: the authenticator gives the user the seed value \(P[0]\) ,computes \(P[N+1]\) relative to the user and saves it to the db. Then, to check if \(P[N]\) is valid, the authenticator simply computes the hash value of \(P[N]\) to check if the result is the value stored in the db, that is, \(P[N+1]\). With this approach for every authentication the authenticator needs only to perform only a single hash computation.
Graphically we get,
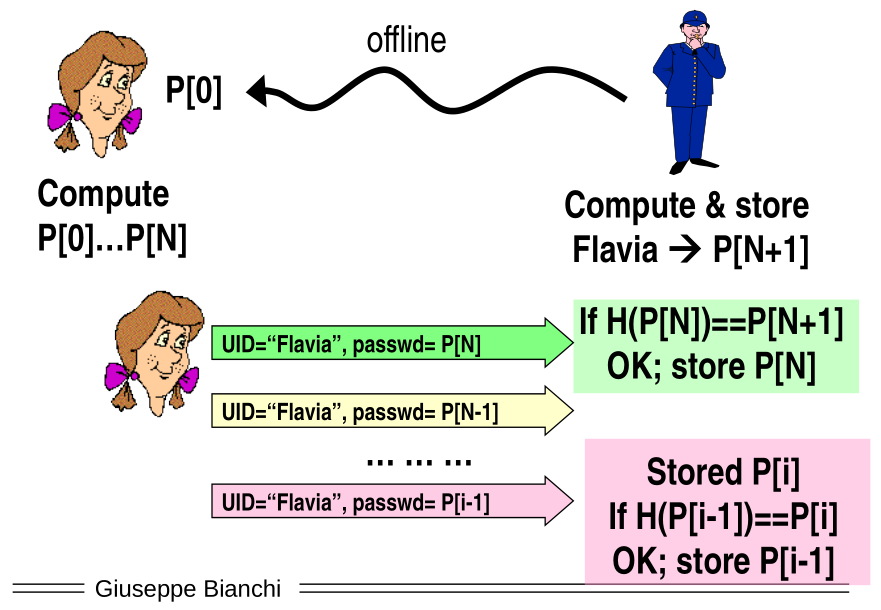
The problem with this approach is that you can get desycnronized, meaning that sometimes you can lose some passwords for network connectivity problems and things like that. To be robust against this type of problem you can define a tolerance window, which defines a specific interval in which the authenticator keeps computing the hash until it is possible to validate the result. For example you could have a tolerance window of 10, and so in the worst case the authenticator has to compute the hash 10 times to validate your password. This technique makes this protocol be more robust to authentication scenario with desyncronization, as long as the desyncronization is limited in width.
To summarise, the benefits of hash chains are:
It allows you tos end your password in clear with no worries.
You can relax the assumption on server-side security, since the authenticator only stores used password and there is no way to predict the next one.
Authenticator only stores 1 value, thus we have the same complexity as in ordinary PAP.
The issues of hash chains are:
Large \(N\) to prevent frequent renegotiation.
Client side is vulnerable, since he must store the password seed or the whole vector of passwords.
2 2-Factor Authentication
Typically OTPs (One-Time-Passwords) are not used by themselves, but are mainly used in 2-factor authentication protocols. In these protocols I don't use only the main password itself as a means to authenticate, but I also use a secondary authentication which adds up to the first one.
With this new setting (2-factor auth) the requirements of OPT change as follows:
One-time authorization token:
generated on a different device (like phone or keycard).
received on a different channel (SMS, email).
Must be human-friendly: The password must be human friendly. This poses some small technical details in how one should properly truncate an hash from a 160 bit digest into 6 to 8 digits to guarantee uniformity.
Different deployment model and relevant assumptions: if both server and clients are assumed to be secure there's no need to use hash chains. With hash chains one can relax the assumption of security on the authenticator side.
There are two protocols for 2-factor authentication:
HTOP, HMAC based OPT.
TOPT, Time based OPT.
Observation: For now think of HMAC as a synonym of Hash, even though they are different things. In the next lectures we will discuss more what exactly is an HMAC.
2.1 HTOP
We assume that both clients and server are secure. The client generates a secret \(K\) which is stored on the server. Instead of computing the hash chain
\[P[N] = H[P[N-1]]\]
I can do the following
\[P[N] = H[K, N]\]
Notice that with this approach, this is not anymore a chain, since knowing \(P[34]\) gives you no information about the next value \(P[35]\). As a consquence of this you don't need to memorize or pre-compute anything and the passwords are infinite. The only thing you need to memorize is the private key \(K\) and the counter number. This method thus does not require pre-computation and reverse order.
Details of HTOP can be found in RFC 4226.
2.2 TOPT
The basic idea is to use time as a counter. For this reason time-based OPT are based on the assumption of having a secure time reference. In this method the counter is computed as follows
\[T = \frac{\text{Current Unix Time} - T_0}{X}\]
where \(X\) is the scale. For example if I want to a single code per day \(X\) will be equal to the number of seconds in a day. Typically few seconds are used. For example Aruba uses \(30\) seconds.
Even with this approach there can still be a tollerance window. For example, it might still possible for you to authenticate at 10.46 with the code of 10.45. For example Delphi uses a \(30\) second slot, meaning that every \(30\) second the code changes, but has a tollerance window of \(1\) minute.
Observation: The larger is the tollerance window, the less secure your system is, but the more usable it is.
How can you make sure that 10.45 on client and server is the same time? For example you can hack candy crush by changing the time of your device. Changing the date is actually a typical attack for these systems.
Details of TOPT can be found in RFC 6238.
3 Mutual Authentication with CHAP
Let us now cover a completely different topic: mutual authentication with CHAP.
Let's assume for the sake of this discussion that CHAP is a rock-rolid protocol and let's try to extend it to do mutual authentication. As we will see, this will create lots of problems. In general the takeway of this discussion is the following critical point: never use a protocol meant for one thing in order to do another thing.
3.1 Using 2 CHAPS
We assume we want to do mutual authentication using the same key. This is very common. For example in the SIM card there is a single identity key for both uplink and downlink. We thus get the following protocol
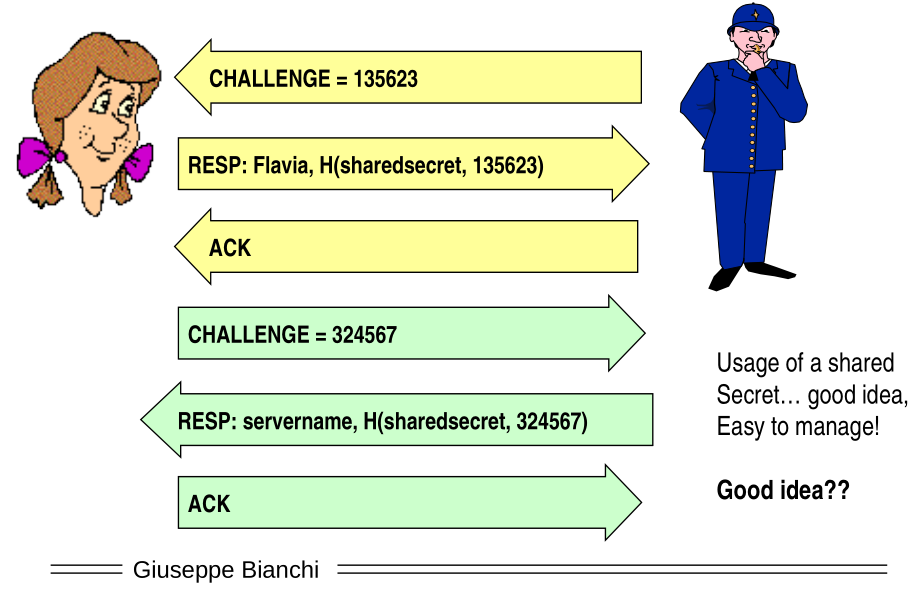
Notice that in the protocol we have shown there is no explicit mechanism which orders the way messages are sent. This vulnerability is exploited in the following basic reflection attack.
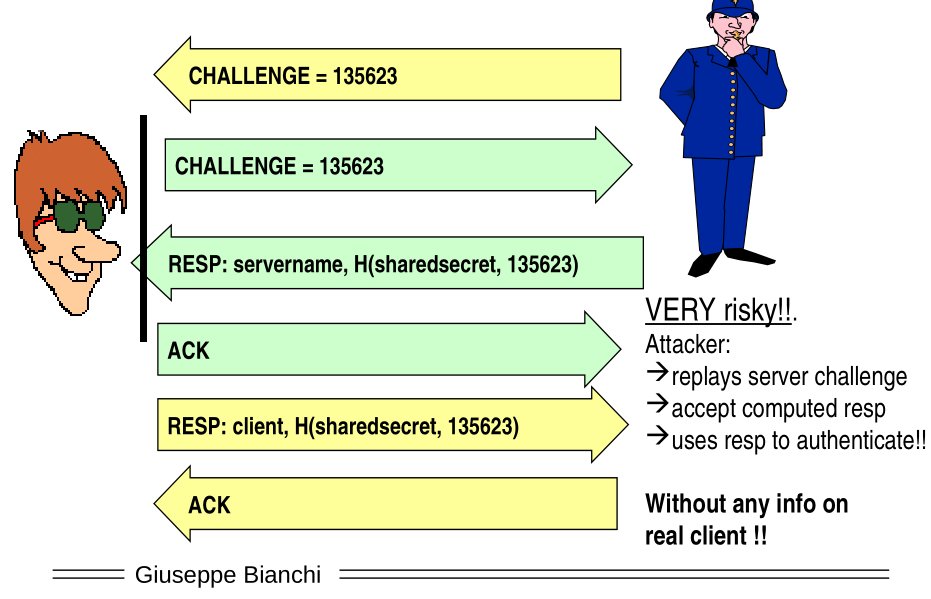
From the pov of the authenticator, even though the challenge he receives is the same one as the one he sent, unless we explicitly mention that a check of this sort has to be done, the authenticator might not even realize this is happening.
3.2 Pippo's Protocol (DON'T DO THIS)
Let us now introduce a new protocol, called by Bianchi Pippo's Mutual Authentication Protocol which combines two CHAP protocols into a single session, so as to not allow the previous reflection attack.
Consider the following exchanges
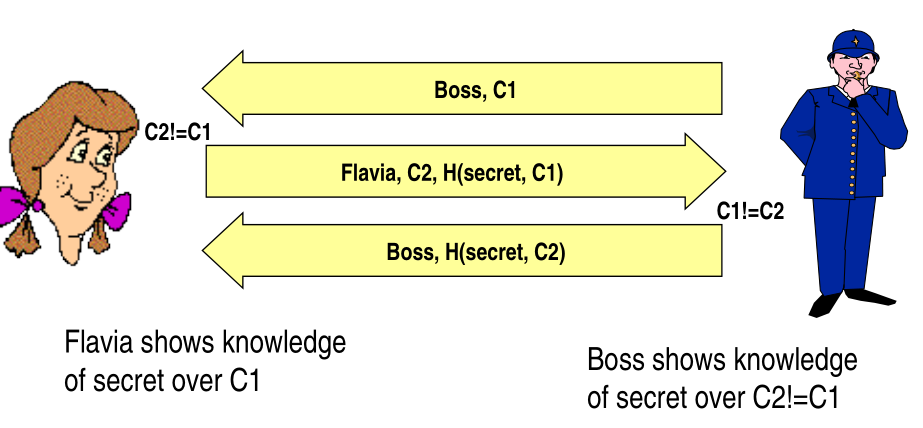
The problem with this protocol is that the check \(C_2 \neq C_1\) is done only on the same session, and it is not done globaly over all the active sessions. The following reflection attack exploits this vulnerability.
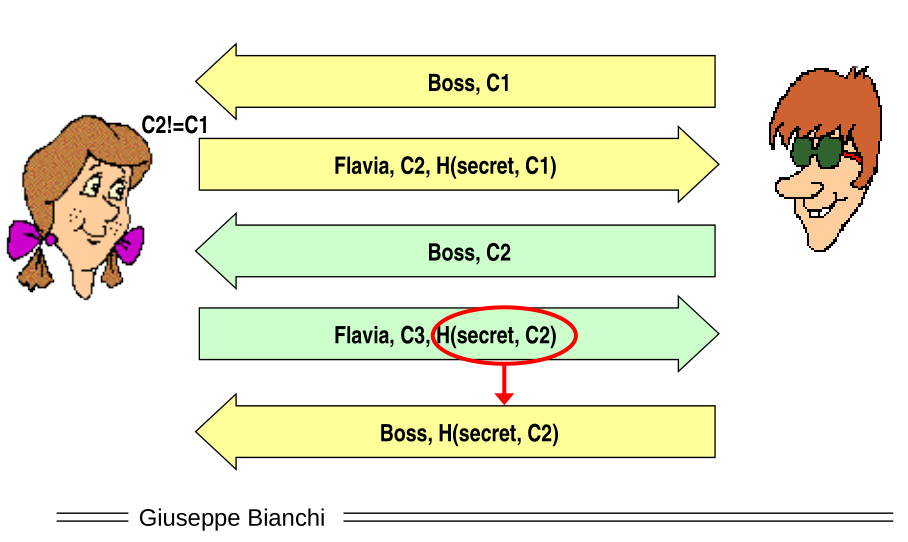
Observation: In this example we see clearly that in security everything that is implicit is nefarious, because its unpredictable and might be vulnerable to some kind of attacks. Security should not be obtained by implicit assumptions, everything should be explicit, because most of the time whatever is implicit is not implemented by the developers.
Even if we fix the reflection attack we can do an intertwining attack.
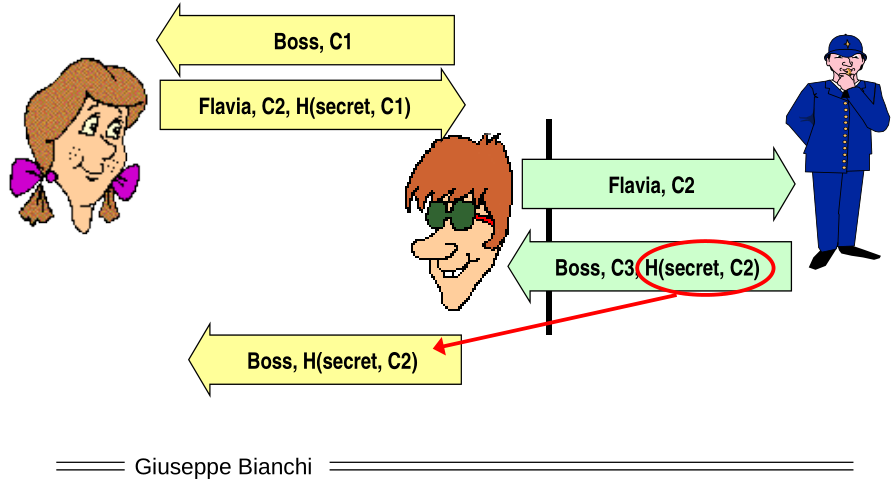
3.3 Working Solution
To finally fix this we have to bind the two directions together by putting the two challenges \(C_1\) and \(C_2\) as arguments of the hash \(H(\text{secret}, C_1, C_2)\).
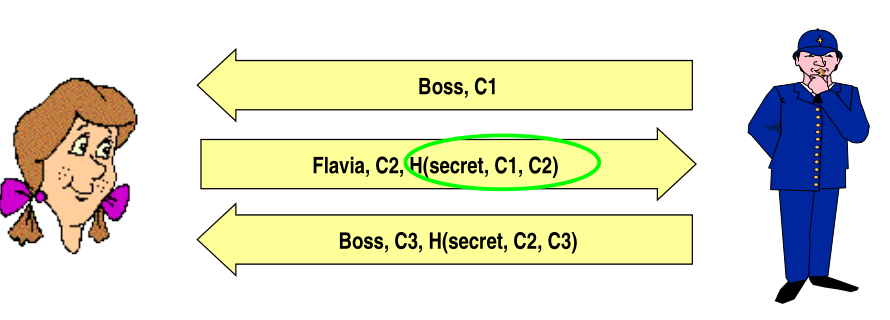
This is still however wrong, because I can do the following
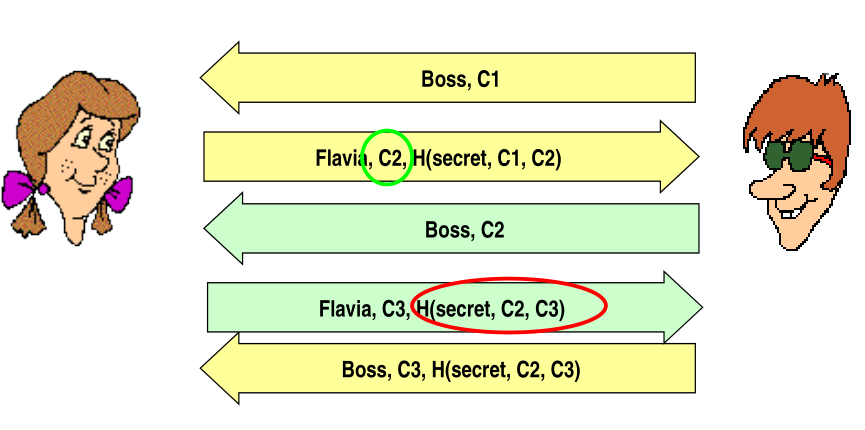
The actual, final solution is to use the same two challenges
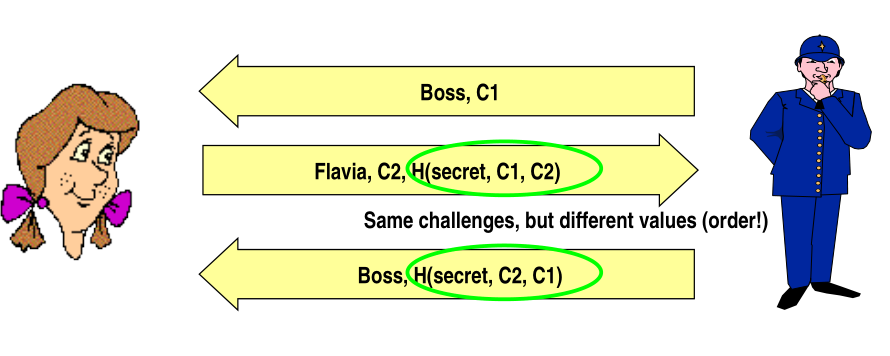
and it works by leveraging the fact that with hash functions if we change the order of the arguments we also change the value of the hash. That is,
\[H(\text{secret}, C_1, C_2) \neq H(\text{secret}, C_2, C_1)\]
Observation: In the final solution we have binded cryptographically the two challenges \(C_1, C_2\) by putting them both in the final hash.
3.3.1 Nonces
We call nonce something that is fresh. It is essentially a generalization of the concept of a challenge. Everytime I want to authenticate I need the knowledge of some nonce.
There are various form of nonce, such as:
Random challenges.
Sequence number. It is not always the case that we need to have random challenges to a secure protocol. When we don't need randomization, we can use a simply sequence of numbers, which is way better, since random challenges repeat in the order of \(O(\sqrt{n})\) for the birthday paradox, while sequence of numbers repeat in the order of \(O(n)\).
Timestamp. Only doable if the timestamp value is obtained in a secured and syncronized way. For example the Galileo software is an advanced version of gps.
To conclude, nonces form a superset of possible challenges.
3.4 Conclusions
Having this example in mind, it is now clear that if we take an algorithm \(A\) meant for a purpose \(P\) (for example authentication), and we use it instead for a slightly different purpose \(P'\) (for example mutual authentication), lots of problems may arise.
In our case the problem of CHAP was the fact that it is defined as a single side authentication protocol. If we use CHAP in a mutual authentication context we thus create two indipendent sessions, which can be exploited in a bunch of ways. To fix CHAP for mutual-auth we created a cryptographic binding of the two challenges, which essentially merged the two sessions together. The final approach can be found in Menezes book under mutual auth prot with shared secret symmetric key, with the only different that inside the hash you also put the name of the two entities (like Alice and Boss).
The conclusion is simple and profoud
Never use an algorithm designed for a purpose for a slightly different purpose.