CNS - 09 - Wireless Cellular Authentication I
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides:
Introduction: We will now see challenge-response authentication protocols used in wireless cellular systems (2G, 3G). We will not cover in detail cellular technology, but for more info look at wireless networks done by Andrea Detti.
1 Cellular Systems
Since 4G and 5G are complex systems, we will look in more detail at 2G and 3G systems. In general in cellular system you must at least have three parts:
Home network: everyone has a specific home network managed with a particular cellular operator, like TIM.
Serving network: If I'm in paris however, and I want to connect to the cellular network, there is someone else that provides connectivity, for example orange.
UE: the particular device that connects to the actualy wireless network.
Note that the wireless network provider might not be the one you are subscribed to. If I go to paris for example I might not find TIM, but rather I can find other networks such as orange. The authentication protocols used must then guarantee that I can enter my login info through orange to authenticate with the TIM operator. Graphically we have the following scheme
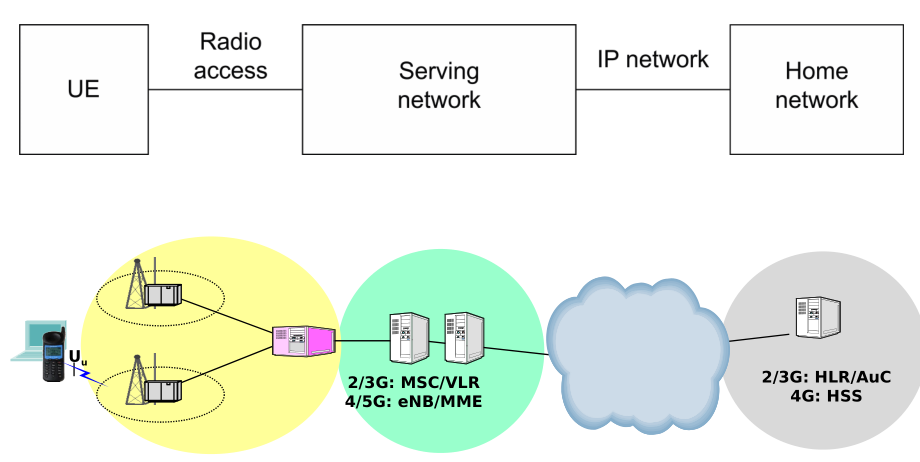
Note for example that a simple PAP protocol does not work, because by definition the service network cannot be trusted completely. This is why CHAP-like approaches have been used to approached autehntication in 2G/3G/4G/5G networks.
2 Authentication in 2G/3G
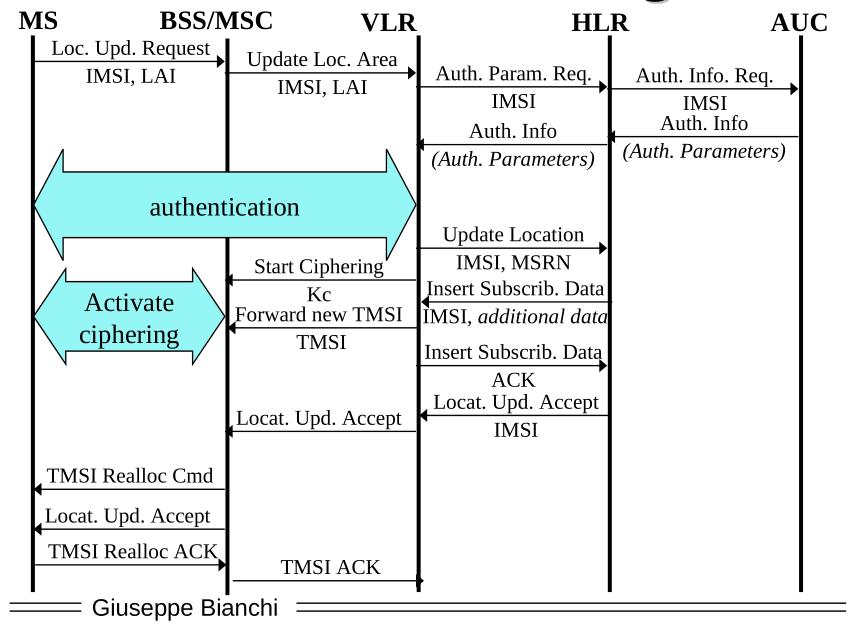
The basic idea is the following: the user asks the roaming network to authenticate with its the network the user is subscribed to. The roaming network asks the home network the data necessary to authenticate the user. This data should not contain the plaintext password of the user. Then, once the roaming network has this, the authentication procedure takes place between the user and the roaming network. After that a key is choosen to start encrypting the data.
Since during the authentication an encryption key is derived, these authentication protocols are also known as AKA, which stands for Authentication and Key Agreement.
2.1 Auth in 2G
Let us now abstract from the technical details, which are more appropriate for a wireless networks class, and go directly to analyze the protocol being used. To do this we will define the following three entities:
The User (MS).
The Service Network (SN).
The Home Network (HN).
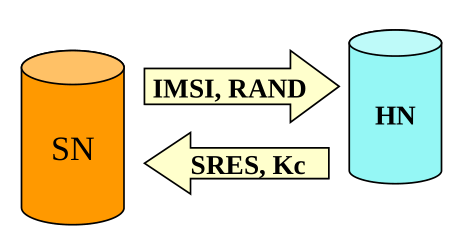
When the user wants to identify to the network, SN sends to HN the IMSI, which represents the name of the user (it stands for subscriber indicator, and is acode that uniquily represents the SIM of the user), as well as a challenge RAND. The HM replies by giving the SN the SRES, which is the proper respond the user should give when challenged with the challenge RAND, as well as the encryption key \(K_c\) that I will use later on.
After that the SN sends the auth request to the user with a specific challenge made up of 128 random bits. The user uses this challenge along with his private key \(k_i\) and a specific function called \(A_3\) to get a 32 bit result SRES. which is sent back to the SN.

Finally the user sends the SRES value back to the SN, which checks it against the value first obtained by the HM. If the two values are equal, then the user is authenticated. To generate the cryptographic key the user uses a different algorithm, called \(A_8\) along side his private key \(k_i\) and the challenge RAND to generate the crypto key \(k_c\).
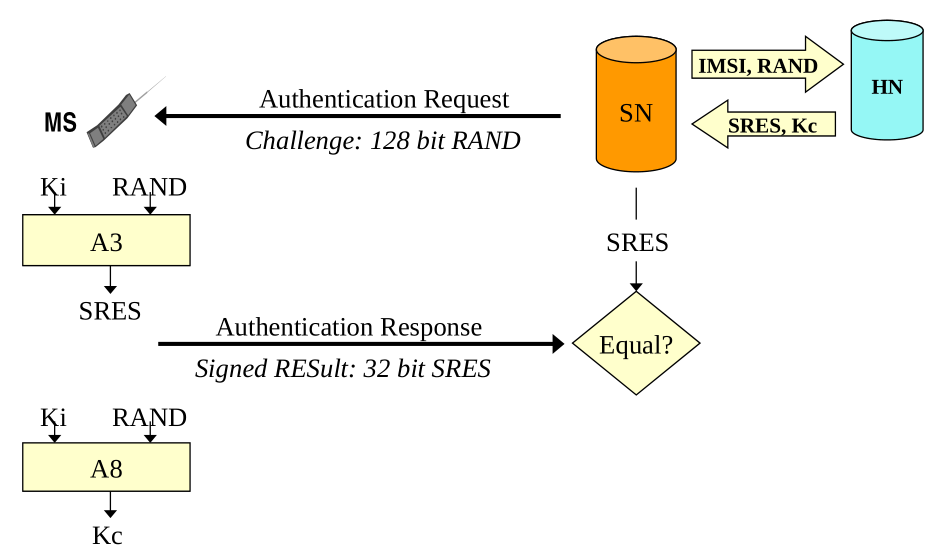
The scheme just described seems two for the following reasons:
You never expose your credentials to an untrusted party.
You never use a pre-shared key for encryption. This is way different with respect to the initial versions of Wi-fi for example, where everyone uses the same pre-shared key. In cellular networks not only every single user will have a different key, but everytime the same user connects to the network, a new key is generated dynamically.
2.1.1 Triplets
Notice that it is extremely inefficient for the serving operator to connect to the home operator everytime the user wants to connect to the network. To solve this problem the idea is that the serving operator only gives the IMSI to the home operator, and the home operator gives N triples of the form \(\langle \text{RAND}, \text{SRES}, Kc \rangle\), each of which allows for establishing an authentication with the given user.
The approach of using triplets (authentication vectors) has two main benefits, which are:
Performance.
The RAND challenge/nonce is generated by the home operator. This prevents a vulnerability in which an attacker enters the serving operator and generates specific nonces.
2.1.2 Security by Obscurity
The algorithm A3 that computes the SRES is computed by the chip inside the SIM, and not by the operating systems of the smartphone. Inside the chip there is also the identity \(k_i\). This means that the telephone does not need to know A3. The only entity that needs to know the algorithm used for authentication is the operator. As a consequence of this, different operators may use different authentication algorithms. From the point of view of security I can hide the algorithm used and keep it for myself. This is exactly the approach taken by authentication by the GSM (2G) guys.
To recap, authentication in 2G was doing using a CHAP-like protocol with
A 128 bitrandom challenge RAND
A 128 bit secret \(k_i\)
An hash using the (proprietary) \(A_3\) algorithm.
Since the key derivation and the challenge authentication were computed using the same arguments (the key \(k_i\) and the random challenge rand), an algorithm called \(A_{38}\) was used to compute both \(A_3\) and \(A_8\) at the same time to get the SRES response (32 bit), and the crypto key of 64 bits (well, technical they were 54 bits plus then 0s).
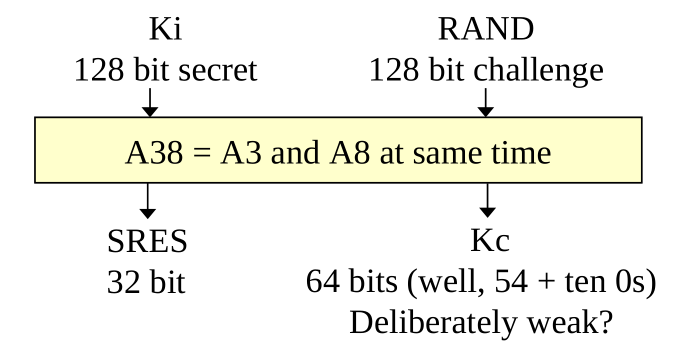
Observation: In 1990s a \(64\) bits was still computationally unfeasible to break, even for governments. But as we have seen, the key used actually only \(54\) bits. And we now that going from \(64\) to \(54\) we are a thousand times less secure.
We'll now get to the crux of the argument: most people still believe that using a secret algorithm is more secure than using a known algorithm. This is called security by obscurity. Security experts however believe the opposite, that is, they prefer known algorithms instead of unkown algorithms.
An example of why security by obscurity does not work as well as we might think is shown to us by the history of 2G, and in particular in how the \(A_3, A_8\) algorithms were used. Since the \(A_{38}\) algorithm could be operator-specific, operators were left with two possibilities:
Either they designed their own algorithm,
or they took a secret algoritm (which was later given the name COMP128) designed by the standardizer and kept secret.
The COMP128 algorithm was never officialy disclosed, but sometime later it was leaked out. In 1998 David Wagner analyzed the algorithm and broke it in minutes. This show us a crucial thing to remember: an algorithm that is not designed by a cryptographer will probably be broken. In 2002 people found out another attack which worked in less than 1 minute (GSM cloning).
This example showed just how much security by obscurity that does not work for various reasons:
It's not easy to find a very strong cryptographer in "restricted" team. (Like Enrico Fermi for the atomic bomb).
If you have a public algorithm, then this algorithm will be read by all of the big guys in crypto, who will try to break it in all the possible ways. In general if an algorithm survives public scrutiny, then the algorithm is probably well designed.
For these reasons security by obscurity has been abandoned by serious people. This is the same divide that there is between closed-source or open-source. In general in the context of cryptography openness is much better.
Observation: the key \(k_i\) works like a master secret from which other secrets derive. This approach of using a master secret is favorable, since we only have \(1\) long term secret (\(k_i\)), while the key actually used \(k_c\) is derived dynamically for every session.
2.1.3 No Mutual Authentication
One of the problem of 2G authentication was the fact that there was no mutual authentication. This means that you could set a fake base station and convince the users to connect to your base station.
To create 4G and 5G stations you need to pay around \(1000\) euroes to have some software defined radios (ETTUS B210). At the time of 2G devices like ETTUS B210 were not available, and thus it was not possible to simulate a base station.
To protect against this type of attack, mutual authentication was needed. The main innovation in 3G and 4G/5G was to change the authentication protocol and come out with a mutual authentication and key agreement protocol.
2.2 Auth in 3G
The difference between 3G and 2G are:
Optimized authentication
Guarantee freshness for auth parameters
More keys and several extra detauls
Instead of doing security by obscurity, the algorithms used in 3G were firsts scrutinized by research community, and then selected. If you want to read more considere the paper from Kasia nyberg that presented those algorithms to the community.
Moving from 2G to 3G, the overall scheme does not change too much
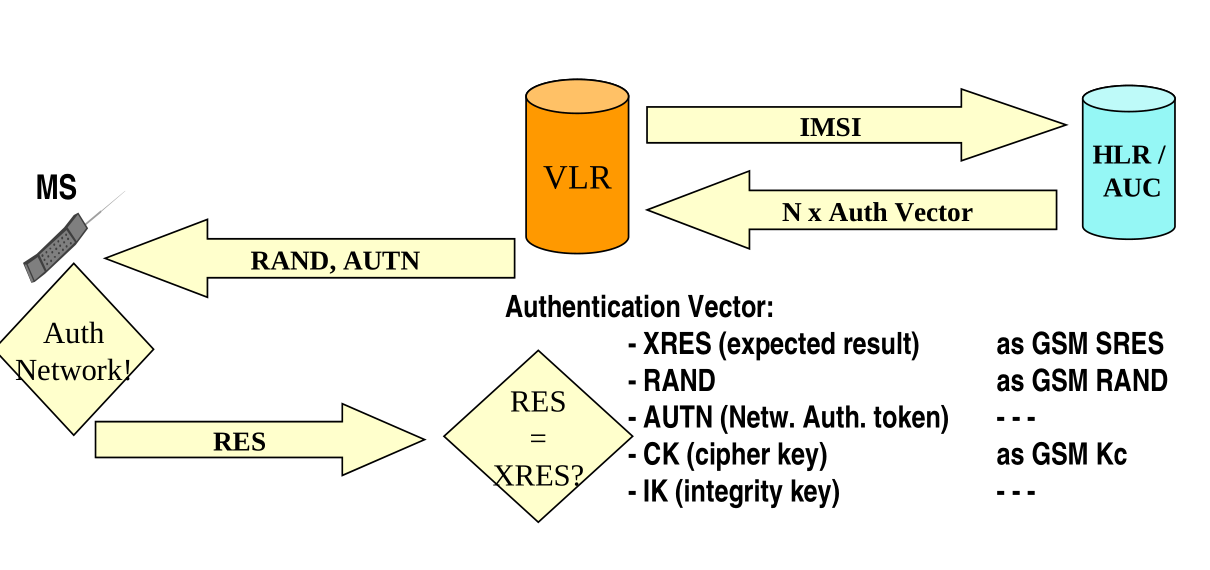
The difference is that in 3G the authentication vectors are quintples, which contain:
The Expected result XRES (Expected Result), as GSM SRES.
The nonce RAND as GSM RAND.
AUTN (Ntw. Auth. token).
The cipher key CK, as GSM Kc.
IK (integrity key)
Notice that in 3G we have a separate key which protects the integrity of our data. (Remember the mistake made in 802.11 when they used the same key for encryption and for integrity). The AUTN is the network authentication token, which is what is needed to prove that the network is authentic.
If you take a closer look at the protocol showned above, a problem may seem to arise: the user does not send a challenge. How can the network prove its authenticity, if the challenge is not sent by the user? In the next lecture we will answer this question, for now it suffices to say that the protocol is actually secure, and the answer to our question lies within the contents of AUTN.
To finish off, the the algorithms used in G3 are called \(f_2\), \(f_3\) and \(f_4\). All of these algorithms depend only on the secret of the user (K) and the random value (RAND) used as a challenge.
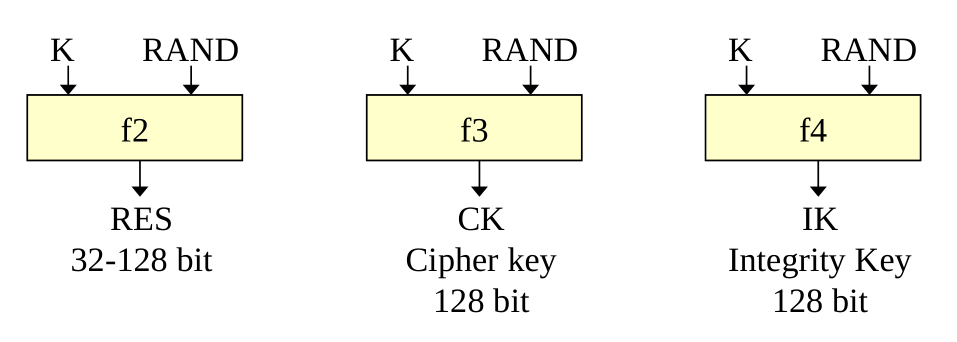
The functions \(f_2, f_3\) and \(f_4\) are completely known and public. In principle you are not forced to use them, but most operator use them because its simply more efficient to use them. Remember though that if you want to use a custom algorithm then your company needs to manufature the SIM cards.