CNS - 10 - Wireless Cellular Authentication II

If the user wants to check the authenticity of the network, conceptually he'd have to send a nonce to the roaming network (VLR). The bright idea used in 3G was that, instead of using a random value as a nonce, a sequence number was used as an "implicit" nonce.

The SQN-MS counter increments by \(1\) everytime an authentication is done and is used for exactly this purpose. For every SQN-MS that resides on the user there is a relative counter, named SQN-HE, that resides on the home network. If everything goes fine then SQN-MS and SQN-HE are syncronized, which means that I don't have to send SQN-MS to the roaming network, because the home network (HLR/AUC) already knows my value.

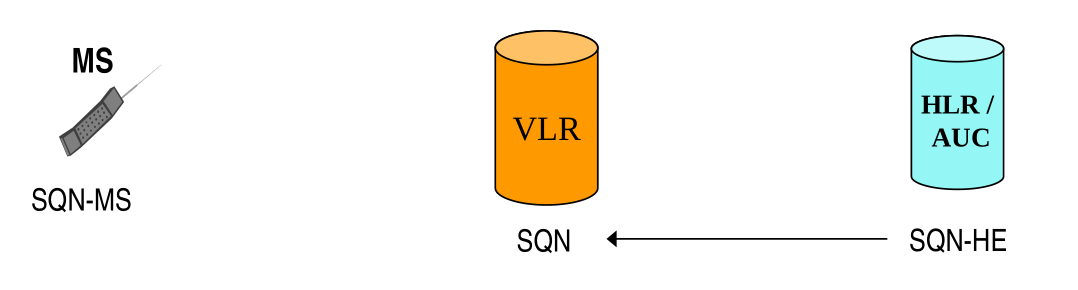
Whenever we want to authenticate the network, the sequence number SQN given by the home network to the roaming network is added in the AUTN message. To check the validity of the network then the user has to check if \(\text{SQN} = \text{SQN-MS} + 1\), or, more appropriately, the user has to checks if the sequence number is greater than the number I'm expecting. Whenever it is inferior however it means that someone might be doing a replay attack and so we don't accept the auth attempt.

With this we are proving knowledge of the secret key \(k\) over the sequence numbers, which is used as if it were an implit challenge. More specifically, we're proving that the roaming network (VLR) is behaving on behalf of our home network (HLR/AUC). From the point of view of the user you don't trust the roaming operator, but only the home network.

The critical points of this approach are the following:

• The counters in the user device (MS) and the home network (AUC) must be (approx) syncronized.

• Robust procedures must be in place to ensure resyncronization.

The AUTN message has the following structure

which can be described as follows

• SQN (Sequence number), 48 bit

• AMF (Auth & key mgmt field), 16 bit, carries information bits on which kind of algorithms or key to use, if the choice is available, as well as the sync window and various signalling informations. This part is of interest to the system level part, but not to the security aspect.

• MAC-A, which is a 64 bit value obtianed by comptuing

  \[f_1(\text{K}, \text{SQN}, \text{AMF}, \text{RAND})\]

  where \(\text{SQN}\) and \(\text{RAND}\) are the two challenges, and \(\text{K}\) is the secret. This represents the actually proof of knowledge of the secret. Notice that a crypto binding is created between the two nonces: the sequence number, which is used to authenticate the network in the eyes of the user, and the rand challenge, which is used to authenticate the user in the eyes of the network.

Notice that SEQ is an implicit challenge because there is no need for the user MS to send SEQ to the VLR, since the VLR can just directly reply back it back to the user. Actually, if the world was in perfect sync, the VLR would not need to send SEQ, since the MS and the home network could be completely syncronized. The SEQ is actually explicitly sent by the home network for various reasons, such as:

• Protection against replay attakcs based on desyncronization issues.

• Protection against DDOS attack in which the attacker modifies the size of the windows so that we would try up to 5000 sequence numbers.

Observation: Notice that the version of the protocol we've described the hash of the sequence number is not done in the reverse message. Technically speaking its a vulnerability. It was decided to do this for network compatibility. It is not a big deal however because in 3G/4G/5G networks the authentication starts from the access point.

In 2G the IMSI value can be used as a persistent indicator to track you along the various networks you connect to.

In 3G instead we have TMSI, which changes at each authentication. This makes tracking much more difficult, because every connection seems to be made by a different person.

In 5G they solved the only vulnerability with 3G, which is the fact that initially the IMSI is sent in plain-text.

Observation 1: iPhone is more resistent than any other telephone against IMSI catching attacks.

Observation 2: The usage of disposable identifiers is possible in Wi-Fi. You can use randomized wifi addresses. If you want to avoid that someone recognizes you by the repetition of your MAC address, you can randomize your addresses.

Notice that even if the TMSI changes everytime, if nothing else is changed then the SQN could be used to track the TMSI, which would violate the location privacy.

There are two possible solutions for this problem.

In principle, I may not even transmit the sequence number and use it as really implicit. This solution however has several drawbacks, which we already mentioned.

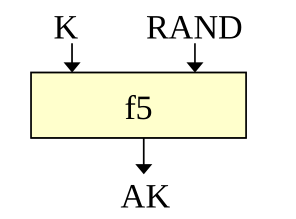
Another solution is to encrypt the sequence number with an apparently random pattern \(A_k\) obtained from the secret key \(k\) on both sides of the authentication process. This works because, in the assumption that both parties are authentic, then both parties already know the secret \(k\). The value \(A_k\) is obtained by using the function \(f_5()\) with \(k\) and the random challenge RAND.

The communication then is described as follows:

1. The home network first sends the challenge RAND and then the packet containting the following

   

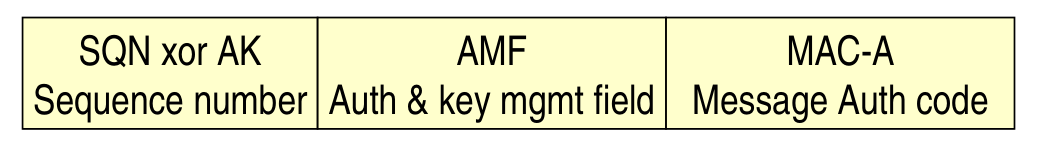
2. The user reads the RAND and computes the 48 bit anonimity key \(A_k = f_5(k, \text{RAND})\), which then uses to decrypt the SEQ number.

   

3. The user then reads the rest of the packet, computes

   \[f_4(\text{SEQ}, k, \text{RAND}, \text{AMF}) = \text{MAC-A}\]

   and compares the result obtained with the value given passed by the roaming operator.

So far by analyzing the 3G auth protocols we have learned the following things:

• Mutual authentication in 3G.

• Usage of sequence as nonce.

• Anonimity Key, and how to generate dynamically run

• TMSI vs IMSI