CNS - 11 - Message Authentication I
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: CNS 11 - Message Authentication
Introduction: In this lecture we started the discussion on how to provide the authenticity of our messages.
1 Message Integrity
In this lesson we will learn:
What we need to do how to authenticate a message.
How subtle is the real world of applied cryptography. In particular we will see that you shouldnt use an hash function to do message authentication.
Integrity means message authentication which is different from user authentication, since in user authentication I need to prove that I'm who I say I am, while in message authentication i need to prove that the message has not changed. In general
\[\text{confidentiality} \neq \text{integrity}\]
since,
Confidentiality: Takes care of hiding the true contents of a message to make sure that only the legitimate destination is able be able to extracts and see its content.
Integrity: Also known as message authenticity, it make sure that nobody should be able to modify a message while in transmission. Only the legitimate source should be able to forge a message.
In certain contexts, for example when writing a cv, you only want integrity and not confidentiality, because you want to make sure that your CV is only modified by you.
While encryption always offers confidentiality, it does not always offer integrity, as the following examples show:
Stream cipher: One time pad is the best possible cipher, but it does not offer any integrity.

Block cipher: ECB with explicit IV per block to make it semantically secure. In this case we may not be able to change the internal bits, but we can change the placement of the text.
There is a stronger class of crypto algorithms, called AEAD (Authenticated Encryption with Associated Data) algorithms, which are a special case where the encryption covers both confidentiality and integrity. In TLS v1.3 they have forbidden to use encryption algorithms that are not AED. This is a very strong requirement. AES-128 and AES-256 encryption only covers confidentiality, while AES-GCM and AES-CCM instead are AED algorithms which offer both confidentiality and integrity.
2 Msg Auth with Symmetric Key
To authenticate a message using a symmetric key, both the sender and the receiver must have an integrity key \(k\), which is different from the cipher key used to encrypt the messages.
To check the integrity of the message we have to add a tag after the message. The tag is a possibly short code which is generated using a secret key and the message itself. The tag itself should not be reversible, and should be uniquely identify the contents of the message, such that if the message is changed, even a little bit, the tag is completely different.
The overall scheme used is the following
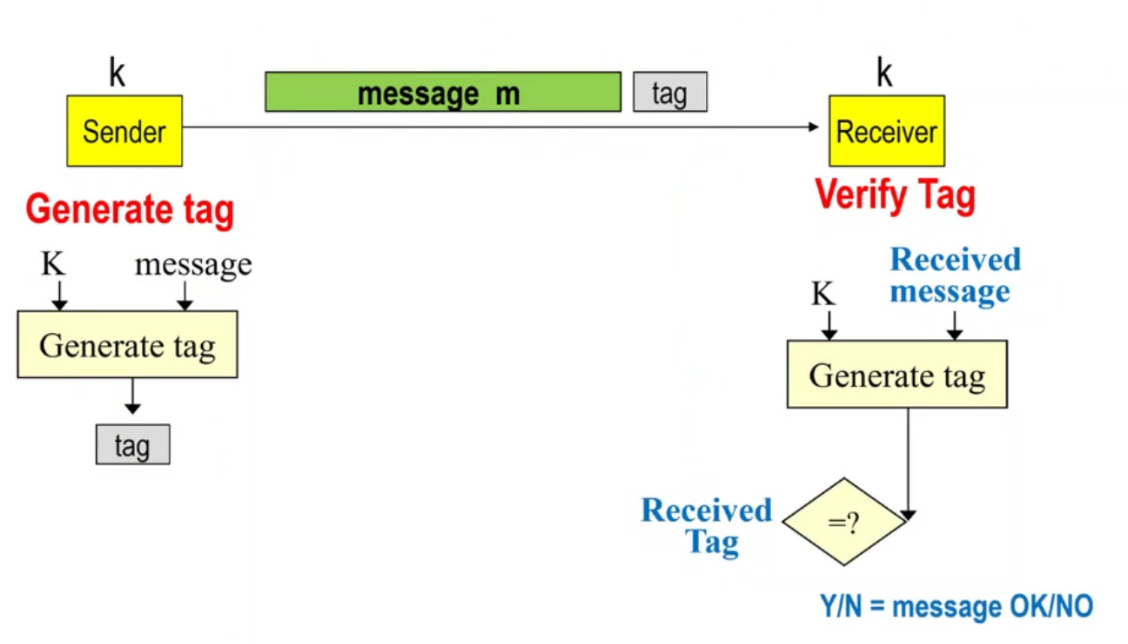
The idea is that the sender and the receiver share a secret key \(k\). When the sender wants to send a message \(m\), he uses a cryptographically strong function to generate a particular tag \(t\). The tag is then sent along with the message, and when the receiver receives the message with the tag, he once again generates the tag using the secret key \(k\) plus the content of the message and and then checks the tag computed with the tag sent by the user. If the two values are equal, then the message is authentic, otherwise the message was either modified by someone else, or was directly sent by a third user (i.e. a non authorized user).
Note that the function has to be such that if an attacker gets to know the plain-text message and the tag, he still cannot go back and find the secret key \(k\).
In general a MAC (Message Authentication Code) adds bytes to the message. You cannot have a message authentication scheme that has \(0\) overhead.
2.1 Digitial Signature
A message authentication code is a form digital signature, but it is weaker than a digital signature, because with a digital signature (DS) nobody can modify the message other than the sender, while in a message authentication code we have two parties that can modify the message: the sender and the receiver.
The digital signature offers the extra non-repudiation property, which in network terms is called source authentication, which describes situations in which the source of a message cannot repudiate the message, i.e. he cannot say that he did not write the message and that the message was forged by someone else.
To support digital signature a new paradigm of cryptography is needed, called public/private key cryptography or asymmetric cryptography.
2.2 Defining Security for MACs
The concept of security for a message authentication code take the form of unforgeability, which states that an attacker should neither be able to create a message, nor to modify an existing message, even with a random modification. Finalyl, this also means that the attacker should not be to extract a key from the pair \(\{M, \text{TAG}(K, M)\}\).
Formally we define unforgeability with a game using a specific attacker model, which can be one of the following:
Known Message Attack: The attacker is given a number of past message/tag pairs
\[(m_1, t_1), (m_2, t_2), \ldots, (m_k, t_k)\]
Choosen Message Attack: The attacker has access to an oracle which gives him pairs of \((m, t)\), where \(m\) is a message choosen by the attacker and \(t\) is the relative tag.
Adaptively Chosen Message Attack: Like a choosen message attack with the difference that instead of having to choose at the beginning of the attack, the attacker can choose whenever he wants to generate a new \((m, t)\) couple.
To offer unforgeability our MAC has to make sure that in all these attacker models the attacker must be unable to forge a tag \(t\) for a general message \(m\). What we mean with "unable to" is not mathematical impossibility, but rather that the probability of forging the tag \(t\) is negligible, i.e. that is the problem of generating the correct tag is computational unfeasible.
Observation 1: The minimum size tag that is used in practice (ippsec) is \(96\) bits. Even \(64\) bits can be enumerated and are not secure.
Observation 2: Note the difference of this definition with the definition of security (semantic security) that we gave for encryption. In particular for encryption we asked that the attacked had equal probability to guess between two messages \(m_1\) and \(m_2\), while in this case we ask that the attacker has negligible probability to forge a new tag for a given message.
2.3 Protections of MACs
A good Message Authentication Code protects from the following types of attacks.
2.3.1 Man in the Middle (yes)
Notice that message authentication protects from a MITM (Man in the middle) attack. Notice that when we talk about MITM there are two aspects to consider:
Networking part (ARP-Poisoning, DNS-Spoofing): This is trivial to do, and its very simple to make sure that your packets pass through my computer.
Message content part: This is harded to do, since it conists in changing the message.
Indeed, suppose an attacker wants to spoof a message from a real user. Even if he captures a message \(m\) and modifies it to obtain a new message \(m^*\), if the function \(F(\cdot)\) used to compute the tag is cryptographically strong, then we have that
The attacker is not able to see \(m\) and \(t\) and invert \(F(\cdot)\) to obtain \(k\).
The attacker cannot compute the new tag \(t^*\) such that
\[t^* = F(m^*, k)\]
That is, he cannot compute the new tag.
The attacker cannot change the message \(m \to m^*\) such that
\[F(k, m) = F(K, m^*)\]
2.3.2 Message Spoofing (yes)
When we use the term "to spoof" we mean to create a new packet with different fields, like source IP address. Anytime a message is created from scratch we have a message spoofing attack.
Message spoofing can be solved with a MAC, because if \(F(\cdot)\) is a cryptographically strong function, then it should not be possible to compute \(F(K, x)\) without knowing the secret key \(k\).
For example, consider DNS. Such protocol is a plaintext protocol, meaning its messages are sent in plaintext, and anyone can send you a message claiming to be the DNS google server. To actually prove that a message was sent by the google server, a MAC service can be used do add a tag to the message.
Observation: A new protocol, named DNSSEC is a more "secure" version of DNS. Its adoption however has been really slow, since introducing crypto always makes things more complex and slow.
2.3.3 Replay attacks (nope)
Even with a MAC, you are still not secure against replay attacks.
Suppose I want to do two transactions with the same \(1000\) dollars. If we send two identical message we will thus have two identical tags. This means that an attacker could simply transmit again my message, and the MAC is not enough to tell the bank which transaction I actually want.
In the case that the messages generated by the application are guaranteed to be different, then this replay attack is practically not a problem. But even in this case, it is always better to implement a security layer against replay attacks at the level of the protocol, because doing it at the level of application may not always work consistently over time.
To prevent replay attacks we can add a "nonce" to each packet. The nonce is then used for the computation of the tag.
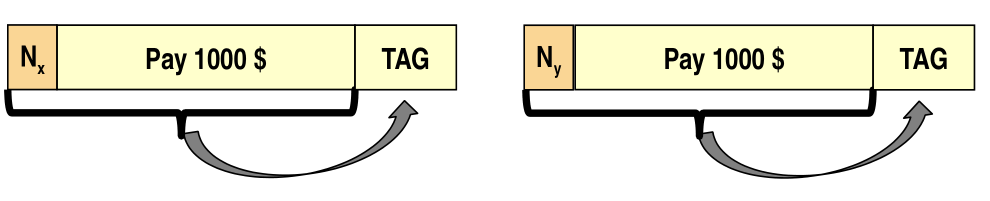
The possible types of nonces are
Sequence numbers (preferred by Bianchi). This type of nonce is extremely conveniente to check for validity, but careful considerations must be taken for how to manage reboots? This means that if you are trying to break a system that uses sequence numbers, you should look into how the system manages reboots.
Random numbers. With random numbers you don't have the problem of reboots, but how can you control that the packet is a fresh one? An approach could be to keep an entire list of the random numbers used.
Timestamp. The problem in this approach is understanding who guarantees time: "now" is really "now"?
Observation: We don't change key for each packet because then reproducibility is a problem with packet loss. What we do instead is a process of changing dynamically the key at every session. If we change the key at every restart, then reboot is no longer a problem for the managing of sequence numbers.
3 Ingredients for MACs
The basic ingredients for MAC are the following
A good hash function.
In the past we had MD5 (128 bit digest), and SHA1 (160 bit digest), both broken in 2005.
Now we use mainly the SHA-2 family such as SHA256, SHA224, SHA384, SHA512. The number represents the size of the digest.
In the future we will have SHA-3 family, which are constructed using a different approach.
Include a secret in the hash. Since the hash only takes a single message, the idea is find a way to combine the secret and the message to form a special message, and then compute the tag on that special message. Since the attacker does not know the secret, he shoulnd't be able to forge his own tag, even if he has the message.
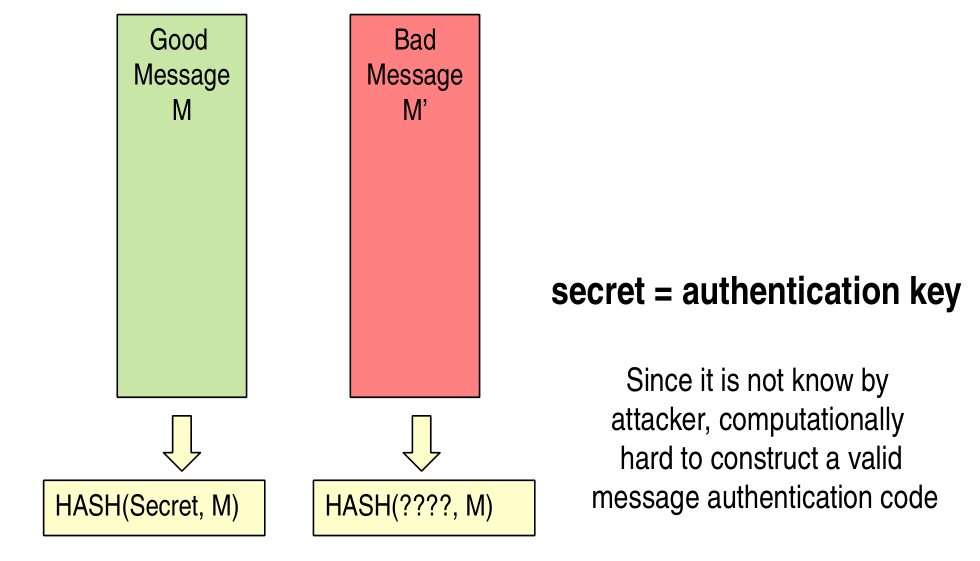
Observation: for bianchi ssh is not so serious with respect to TLS
and Ipsec. In linux the sha256sum command is trivial to use.
echo "HelloWorld" | sha256sum 89c99d37500be2061f853db3a4da2fcce4c0fc0f2f2b71bc2238acca0967c3b7 -
3.1 Where to put the key?
The problems is exactly in the second step: Where do we put the authentication key in the hash? We have various options:
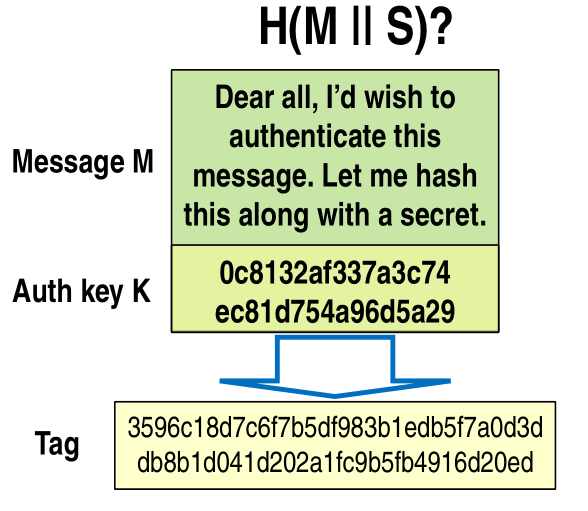
After the message, \(H(M \,\,||\,\, S)\)?
Before the message, \(H(S \,\,||\,\, M)\)?

Some other fancy way?, \(H(K \,\,||\,\, M \,\,||\,\, K)\)?
Why do we even bother asking this question? Well, we would not care about such details if the hash function were the "perfect" hash function, which is known as a random oracle. A random oracle is defined as a black box model in which, given any distinct input \(x\), \(H(x)\) is a truly random value but with the repeatibility property, which means that given the same input \(x\), we get the same output \(H(x)\). Clearly a random oracle cannot exist, and is therefore an idealistic abstraction, since you can't have both of these properties.
To understand where we should put our secret we have to understand better how modern hash functions are constructed.
3.1.1 In the Suffix \(H(M \,\,|\,\, S)\)?
If the hash we're using is constructed in an iterative way similar to the SHA-256 function, then if we put the secret at the end, we would only have to repeat the last compression block to discover the secret.
This is called a pre-computation attack, and it reduces the computational resources for doing a brute-force attack from \(2^{128} \cdot N\) to \(2^{128}\), where \(N\) are the number of blocks in the hash computation.
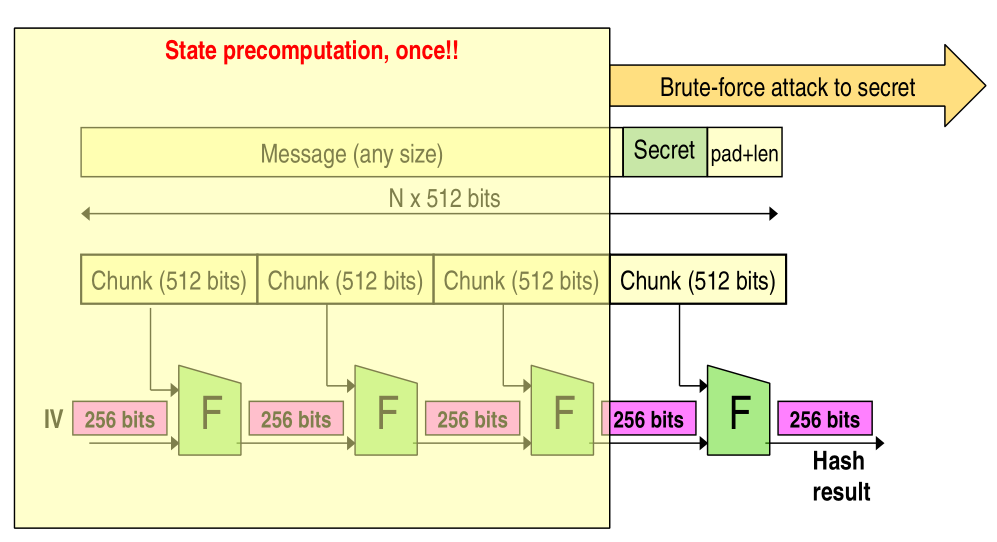
4 Iterative Merkle-Damgard Construction
All the function that we built in the past and today are constructed using the iterative Merkle-Damgard construction. In general its very hard to construct a function
\[f(\text{any size}) \to \text{fixed size}\]
Having said that, crypto guys have found good functions such that
\[f(\text{fixed size input}) \to \text{smaller fixed size}\]
These functions are called compression functions. Let us now see one example of such function.
4.1 SHA-256
Consider a message of \(k\) bits, where \(k\) is an arbitrary value. The SHA-256 pads the message with enough bits so that the overall result is a multiple of \(512\) bits, and at the end of the message in the last 64 bits it places the length of the message modulus \(2^{26}\).

You then cut the message into chunks of \(512\) bit, and you use a known and fixed IV (initialization vector) of \(256\) bits in the following way
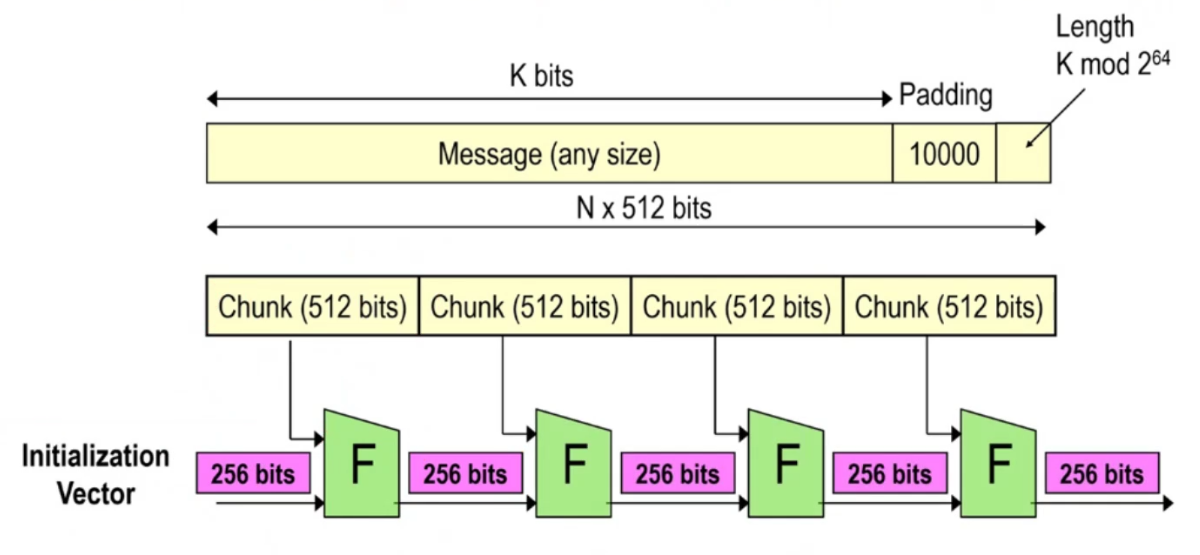
At the end, by applying multiple times the compression function \(F(\cdot)\), we get our hash result of 256 bits. Merkle-Damgard demonstrated in the 1970 that if \(F(\cdot)\) is resistant, that is if \(F(\cdot)\) satisfies the three properties of an hash function, then also the iteration is resistant.
Question: Whats the difference between the Initialization Vector (IV) of an hash function and of an encryption scheme? In the first case it is constant, fixed and known, while in the second case it has to change everytime.
In the particular case of SHA256, the initialization vector is the following
6a09e667bb67ae853c6ef372a54ff53a510e527f9b05688c1f83d9ab5be0cd19
Observation: The computation of a sha hash can be made extremely efficient because we don't need to load the entire contents of the file we're hashing, but we can read it in stream mode and compute the hash chunk by chunk.