CNS - 12 - Message Authentication II

In the previous lecture we saw that putting the secret in the suffix \(H(M \,\,|\,\,S)\) made the system much more vulnerable to brute-force attacks.

If we put the secret the start things get even worse, because we are able to forge a different authenticated message \(M' \neq M\). Indeed, consider the following situation

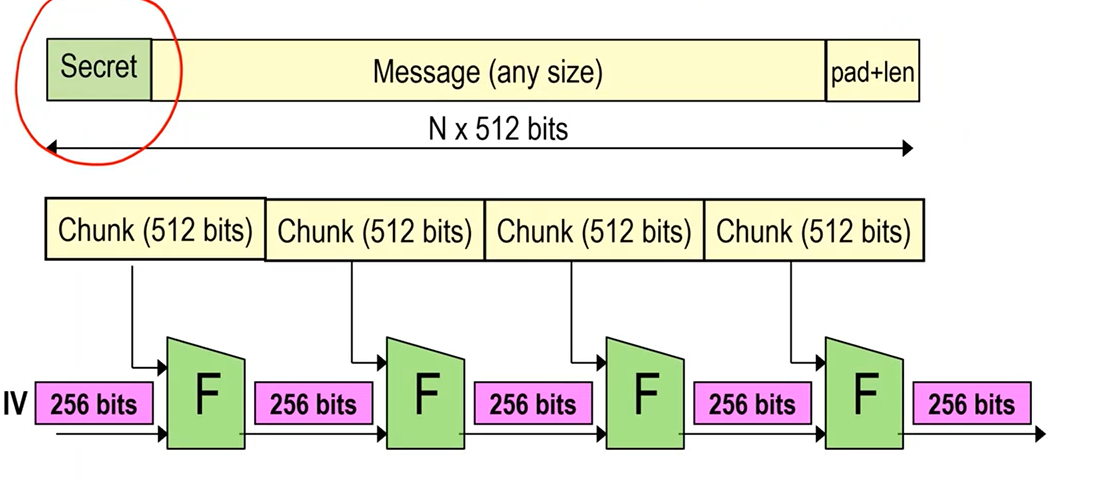
Given that situation we can extend the message with a plaintext+length choosen by us. Once it is extended, we can compute another \(F(\cdot)\) block to compute a valid MAC for the extended message without knowing the original secret.

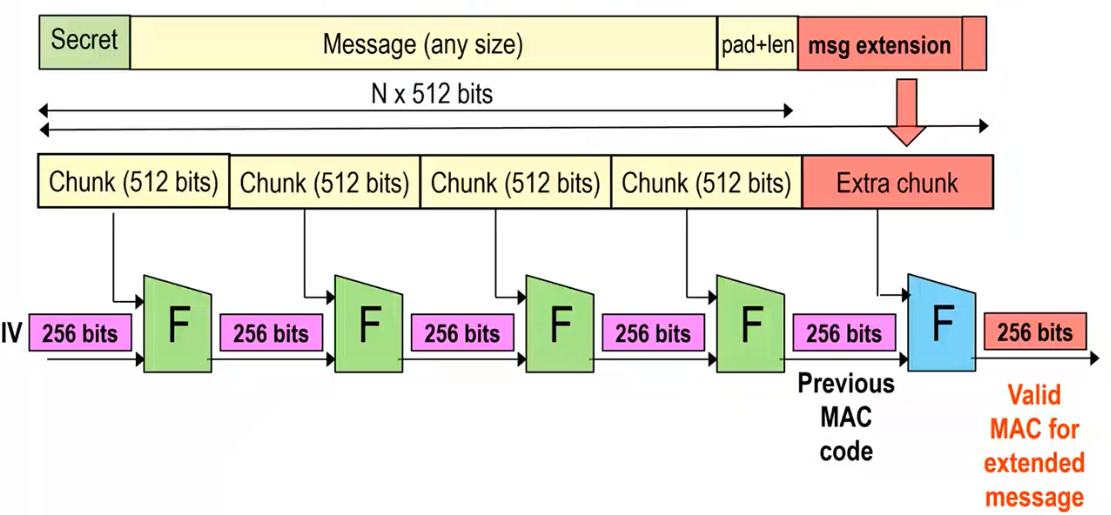
A pratical attack would've to deal with the old padding, but from our pov we don't care, since we already showed it is vulnerable.

Observation: This is another example of one of the most important lesson in crypto: never take something for a purpose and extend it to apply it in another context.

Our goal is to create a message authentication code for a message \(M\) using a key \(K\). To do this we choose an hash function \(H(\cdot)\). Today for example we could select sha256. The HMAC construction can be described as follows

\[\text{HMAC}_k(M) = H(K^+ \mathbin{\oplus} \text{ opad } \,\,||\,\, H(K^+ \mathbin{\oplus} \text{ ipad } \,\,||\,\, M))\]

As we can see, roughly, it seems like we are putting the secret in the prefix of the message. Note however that this is not exactly the case, because, even though the secret is in the suffix of the argument of the external hash, the message is not appended to the suffix in clear, but rather it is the hashed version of the message that is appended. The basic idea then is that with HMAC we are computing the following

\[H(\text{secret} \,\,||\,\, H(\text{secret}, \text{msg}))\]

Let us now discuss the details of the constructor:

• The value \(K^+\) is the shared key extended to the block size. For example, if we use SHA256, the secret is padded with zeros up to 512 bits.

  

• The value \(\text{opad}\) is \(\text{0x36} = 00110110\) repeated as needed to derive the outer secret.

  

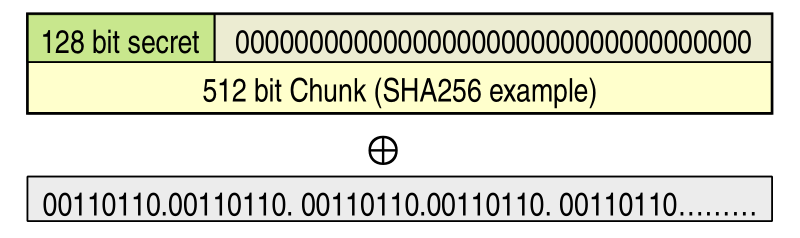
• The value \(\text{ipad}\) is \(\text{0x5C} = 01011100\) repeated as needed to derive the inner secret.

The values \(\text{opad}\) and \(\text{ipad}\) are introduced because, in reality, the inventors of the HMAC technique proved that the best construction, the so-called nested MAC construction (NMAC), actually requires two different secrets, which are combined in the following wayness

\[H(\text{secret}_1 \,\,||\,\, H(\text{secret}_2, \text{msg}))\]

they realized however that for pratical reasons it would've been safer to ask for just a single secret, and so they introduced the two values \(\text{opad}\) and \(\text{ipad}\), which are used to produce from a secret two different strings.

The following diagram helps understand the HMAC construction. The inner hash is performed on the inner key as follows

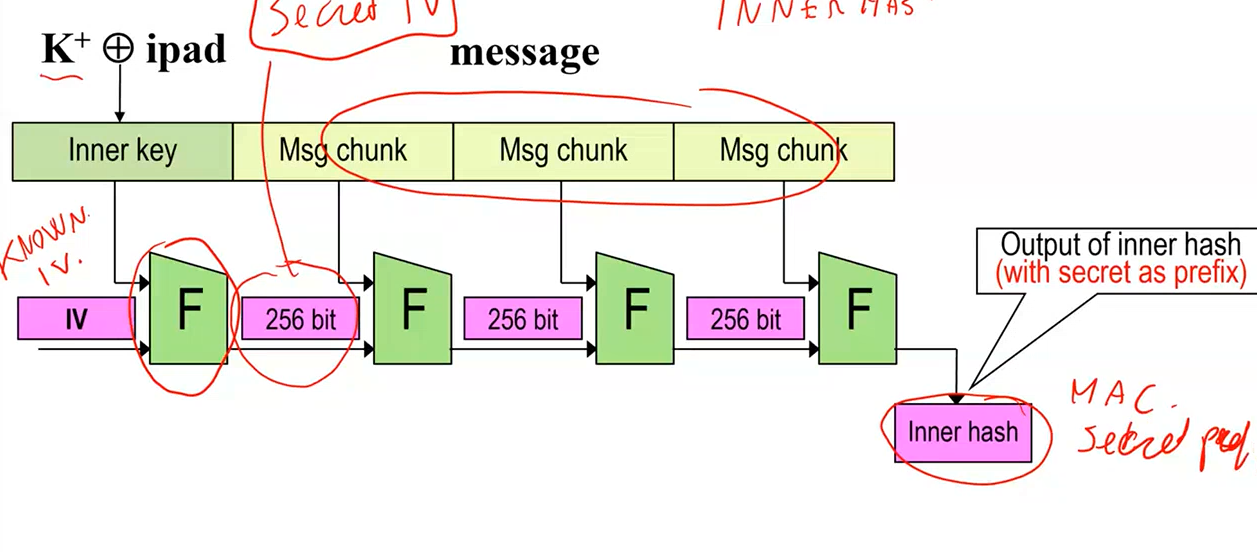
So far so good. We know however that this is vulnerable to the expansion attack. To fix this vulnerability we then place a sort of "barrier" by computing the outer hash as follows

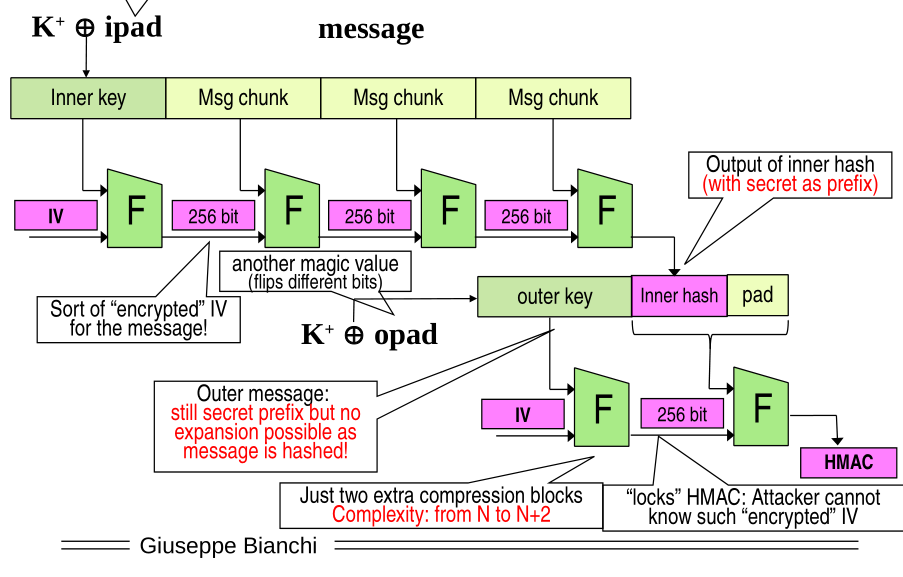
Notice that the complexity of HMAC only adds two more compression blocks to the original

The takeway of all this discussion is that you shouldn't do \(H(S, M)\) or \(H(M, S)\). What you should do is hash the message with the secret and then hash it again.

\[H(S' \,\,|\,\, H(S, M))\]

By hashing the hash we "lock" it in place, because the message cannot be anymore expanded.

For the proof of security you can look at the paper by Bellare, Canetti e Krawczyk. There is actually a funny story in terms of HMAC Security.

In 2005 the hash function MD5 was broken. At that time many HMAC tags used as their underlying hash function the MD5 algorithm, and so one of its creator, Bellare, thought that HMAC-MD5 would've been broken a few months after MD5. Yet, time passed and no one was finding ways to break HMAC-MD5. This prompted Bellare to go back and look at his proof regarding the security of HMAC. In it he modelled an hash function using the following two assumptions:

• That is must generate a pseudorandom output;

• That it must have tha anticollision property;

These, after all, were the standard properties required for an hash function. Yet, when he looked into his proof, he found out that the only assumption he actually used was the first one. This means that, even, if the anticollision property is broken for a given hash function, the HMAC might still be secure.

In 2006 Bellare wrote another paper in which he discussed that the only assumption required was pseudorandomness for having a secure HMAC.

Important: HMAC represents one of the few areas in cryptography where we have a perfect solution for a problem. So, if you ever need to implement a MAC using hash functions, simply use HMAC and do not be creative.