CNS - 14 - RADIUS II
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides:
Introduction: In this lecture we finish off our discussion of the RADIUS protocol by discussing the second vulnerability of the protocol: the way passwords were encrypted.
1 Password Encryption in RADIUS
Suppose the user sends his credentials (username:password) to the nas using a PAP protocol. Now the nas has to send these same credentials to the radius server. Notice however that, even if the communication between the end-client and the nas could be considered to be done over a secure-channel, the same cannot be said for the communication between the nas (radius-client) and the radius server.
The radius protocol thus defined a technique to encrypt the password. Consider a user password, like \(\text{ugo}\). To encrypt it the radius protocol did the following things:
Adds padding to reach \(16\) bytes.
Generate a \(16\) byte hash using the secret key and the content of the authenticator field of the request
\[\text{MD5}(\text{secret} \,\,|\,\, \text{Request Auth}\]
The password is encrypted by XORing the padded password with the hash generated before.
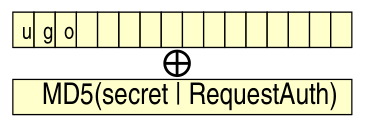
Notice that if the password is longer than 16 characters. Since for security reasosn we cannot pad two blocks with the same stream, the following extra steps had to taken
Compute a different keystream in the following way
\[\text{MD5}(\text{secret} \,\,|\,\, \text{result of previous XOR})\]
XOR with the next segment of the password.
2 Security Weaknesses in RADIUS
First of all, radius is vulnerable to message sniffing and modification:
As far as the message sniffing is concerned, since radius is a clear-text protocol, this leads to potentially significant privacy issues. The only fix in this case is to use a secure communication channel, which can be created with TLS for example.
The message modification vulnerability is much more dangerous, because it leds to the forging of access-requests. The solution in this case is to add authentication to the requests aswell as the replies.
Observation: EAP (Extensible Authentication Protocol) is not an authentication protocol, but this is a protocol that lets you exchange authentication messages. This means that the authentication approach used inside EAP is arbitrary. For example there is EAP-TLS, EAP-AKA. For example, when you connect to the eudoroam network, you use the EAP-PEAP.
2.1 Message Authenticator
In 1998 they included an extra field which authenticated the request packet.
The basic idea is that they standardized a new attribute type \((80)\), whose field contains the authentication tag, which is finally computed HMAC-MD5.
Observation 1: With this fix we only take care of message integrity. Replay attacks of a request message are still possibles, meaning that an attacker could grab a valid message and send it later.
Observation 2: Its very crucial to understand the difference between a vulnerability and an exploit. Bianchi and Giorgio exploited a well known vulnerability in LoRaAWAN. They discussd their findings in a paper at MEDCOMENT 2020.
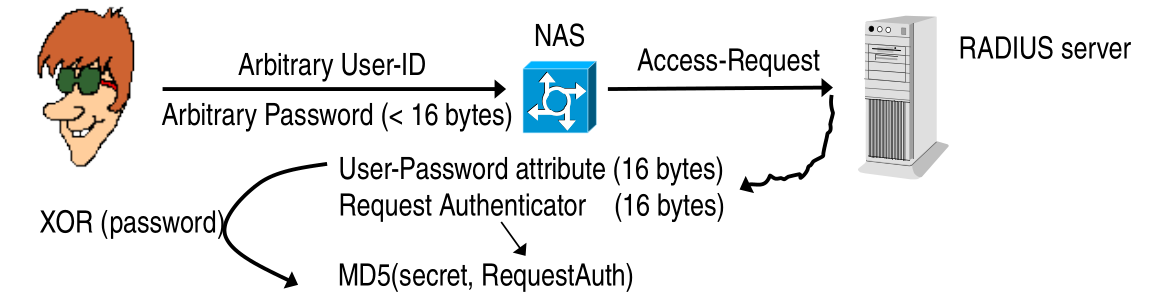
2.2 Dictionary Attacks to Shared Secret
A big vulnerability of the RADIUS protocol is that the secret is put in the configuration of the radius client by the network manager. This means that people usually put a low-entropy strings as a shared secret.
To further decrease the scurity of the secret, many implementations only allow ASCII characters.
Finally, often there is a single secret used for the entire network. There is actually a funny story in here: Fonera radius password hack. To fix this vulnerability you can simply create a single secret key, and combine it to a identifier with HMAC.
To perform an actual offline dictionary attack you can intercept any request-response pair. From this you get everything but the secret to compute the RespAuth field
\[\text{MD5} = (\text{Code} \,\,|\,\, \text{ID} \,\,|\,\, \text{Length} \,\,| \,\, \text{ReqAuth} \,\,|\,\, \text{Attributes} \,\,|\,\, \text{Secret})\]
If you don't access to both streams you can simply you a request with a known user and password (Choosen Plaintext Attack). This is possible only because they used the same secret for authenticating the reply as well as for encrypting the user password. Not a huge advantage, since getting a pair of request-response packets is very easy.
2.3 Dictionary Attack to User Password
To attack the password of the user you can put the name of the victim you want to hack with an arbitrary password. You can then sniff the access-request packet sent by the nas server to get a valid keystream.
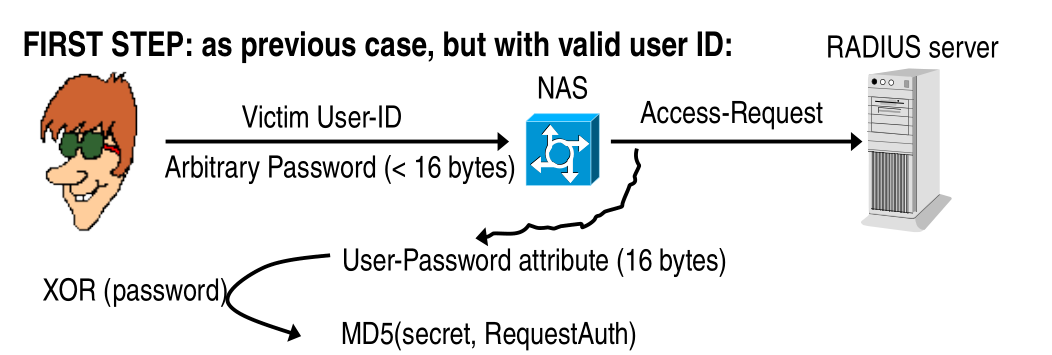
Once you that you can then take the valid request and spoof a number of access-requests all with the same code generated by the nas, bypassing all protection.
3 Poor PRNG Implementations
The security of radius requires the uniqueness of the request authenticator. How do we generate such request authenticator?
To answer such question consider the following question: suppose
you have available a function rand() which generates \(4\) random
bytes, and you have to generate \(16\) bytes. To do this you have
three approaches, which are:
Call the function four times to generate four distinct values.
\[R_1, R_2, R_3, R_4\]
Call the function one time to generate a single \(4\) byte value and fill the remaining space with zeroes.
\[R_1, 0, 0, 0\]
Call the function one time to generate \(R_1\) and fill the space by comuting four times the \(\text{MD}(\cdot)\) of the single generated value.
\[\text{MD5}(R_1), \text{MD5}(R_1), \text{MD5}(R_1), \text{MD5}(R_1)\]
Even though intuitively we'd probably answer the first strategy, the actual answer is the third one. The reason for this is that pseudo random number generators have a specified period, which is the length of the cycle such that the number do not repeat. Typically, non crypto PRNGs of \(N\) bits have a period of \(2^N\). Consider for example the following PRNG
\[0 \to 3 \to 1 \to 5 \to 6 \to 2 \to 7 \to 4 \to 0 \to 3 \to 1 \to \ldots\]
Notice the period of this PRNG is \(8\), and thus it uses \(3\) bits. Now, suppose we merge four subsequent pseudo-random numbers generated with this PRNG. We'd have that
The first packet would have \(0, 3, 1, 5\)
The second packet would have \(6, 2, 7, 4\)
The third packet would have \(0, 3, 1, 5\)
So we started with a PRNG with period \(8\) and we found a repetition after \(2\) packets. We basically dropped down the period of a factor of \(4\), because we aggregated \(4\) numbers together. You thus don't want to include too many subseqeuent numbers generated from the same seed. If we define security in terms of the probability of repeating, i.e. after how much we see repetition, we have that
The first solution repeats after roughly \(2^{30}\).
The second and third solution repeat after roughly \(2^{32}\).
Most radius implementation were based on non-secure PRGNs. Even if a PRGNs passes statistical tests such as Kolmogorov-Smirnov tests and so on, they still might be poor from the pov of security. Often non-secure PRGNs have the following weaknesses:
Predictabiity: Poor-PRGNs are often very predictable, meaning that if I show you a value then you can infer what will be the next value or what was the previous value; Crypto PRGNs should not allow this to be done.
Short cycles: Sometimes it happens that the generator repeats earlier with respect to the maximum given by the number of bits of the PRGNs.
unique values: You should also check if the values generated by the PRGN are unique values or repeated values. If you have a PRNG with a cycle \(2^N\) if the values do repeat then by the birthday paradox your security level is approximately \(2^{N/2}\).
3.1 Linear Congruential Generator
The most common non-crypto PRGN is the so called Linear Congruential Generator, which is defined as follows
\[R_{n+1} = (a \cdot R_n + b) \mod m\]
the values \(a, b, m\) are choosen such that the cyle is maximum. If predictability is not your concern the LCG is a good way to generate a pseudo-random quantity.
3.2 Mersenne Twister
The mersenne twister is another PRNG in which the cycle is \(2^{19937} - 1\), which is basically infinite, but the values do repeat.
3.3 Replay Attack in RADIUS
Given that many RADIUS implementation use poor PRNG, we can infer that auth requests will repeat. This leads to the possible exploitation of a number of replay attacks, such as:
Sniff the network and create a table in which you put the auth request nonce and the access-accept packet.
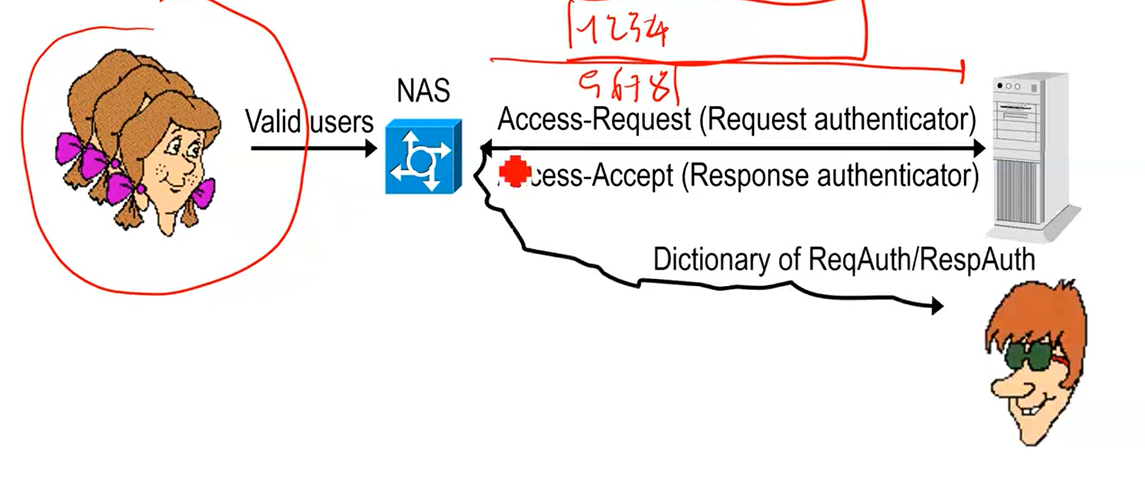
After a while you enter, and if the request contains an already seen nonce you stop the packet and you can directly reply the nas with the access-accept packet you stored in your dictionary.
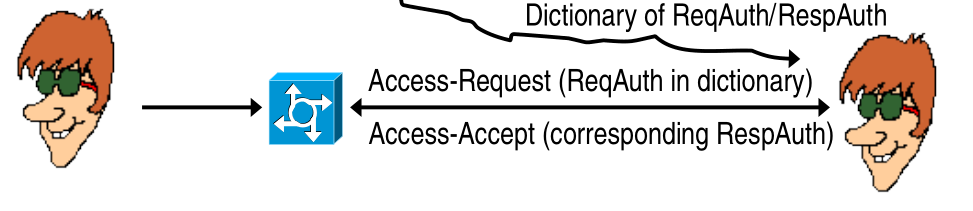
The same type of attack can be done for the user password.
Finally, to attack the passwords of the clients you can transform a passive attack into an active one, in which you can use arbitrary passwords to build your dictionary of nonces (keystreams).
3.4 Final Observations
Some final observations regarding PRGNs:
Observation 1: Having secure PRNGs is one of the most important parts in security. This is why in penetration testing and code analysis the first thing you want to check is how the PRNGs are implemente
Observation 2: The National Institute of Standards and Technology (NIST) recommended to use the following four things:
A particular hash function
A cipher
An asymmetric encryption scheme
A PRNG generator.
In turned out that the PRNG was subtly broken, meaning that it was predictable. This breaks all crypto.
Observation 3: Suppose you were doing a penetration testing knowing the source code, and suppose you find that URL were being generated using the following scheme
\[\text{Base64}(\text{SHA256}(\text{user_email}, \text{RAND}()))\]
remember that \(\text{RAND}()\) is an LCL PRNG, which means that if I know a value I know all the others values. I can thus brute-force the random value and if I know the subsequent emails, I can totally predict the future URLs. This is an example of how to exploit non-crypto PRNGs.
4 Lessons from RADIUS
From RADIUS we have learned the following things:
An application protocol should not include security. The idea is to develop a protocol completely insecure, and then secure it using a protocol specific for security, like TLS.
Remember to avoid including algorithms in protocols.