CNS - 18 - TLS III
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides:
Introduction: In this lecture we will analyze in depth the cbc padding attack, which will make it clear why doing MAC then ENCRYPT is wrong.
1 CBC Padding Attack
We will now see one of the first attacks found in TLS v1.0.
1.1 CBC Padding (TLS v1.0)
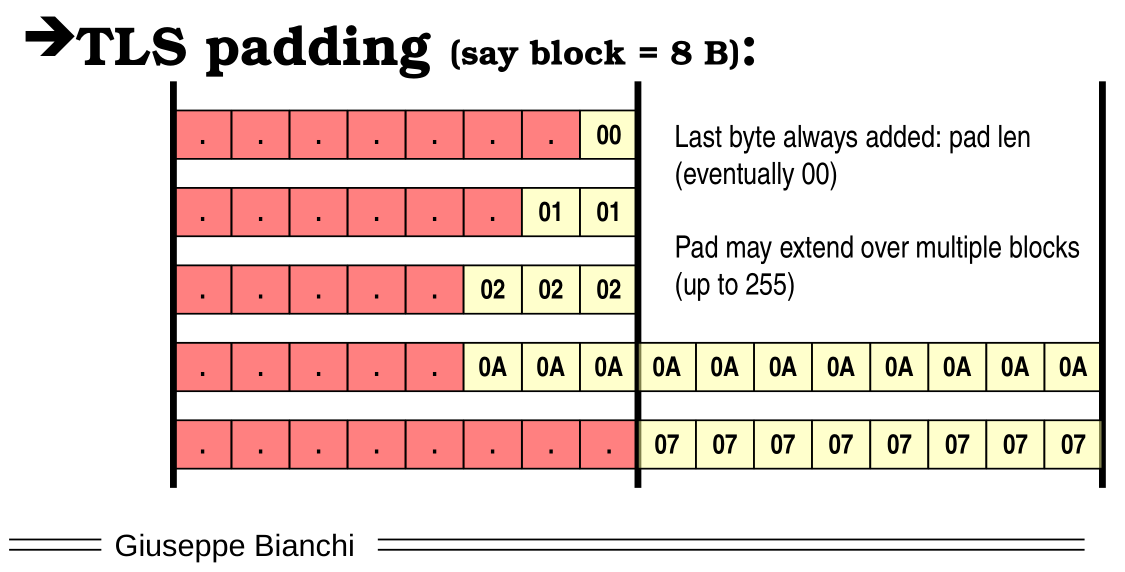
Suppose you want to encrypt the data in TLS using a block cipher. Since TLS first computes the MAC and only then encrypts the data, careful considerations must be taken care when the resulting data + mac does not fit an integer number of blocks. In particular, a certain number of padding bytes must be added in order to fit the last block boundary.

TLS decided to deal with padding in the following way: the last byte of the message represents the number of bytes added for the padding. TLS also decided on the following convention: if the length of the padding was a certain value \(x\), then all the bytes of the padding would've the same value \(x\).
1.2 CBC Decryption (TLS v1.0)
When you receive a TLS packet the following steps have to be taken:
Decryption of the message. In this step the receiver checks whether or not the size of the message properly matches up with the block cipher used. If it does not match up, an alert error message can be sent (decryption_failed). Otherwise it moves to the next step.
Remove of the padding: After the data is decrypted, the receiver checks if the padding is set up correctly. In particular it checks if the length of the padding is present and it also checks whether all the bytes of the padding have the same value as the length itself. If this checks fails, an alert error message is returend (decryption_failed). Otherwise the process goes on to the next step.
Check of MAC: In this final step the server checks the MAC signature. if it fails, an error message is returned (bad_record_mac), otherwise the message is read.
Notice that depending on where the process fails, different error messages are sent back. This is a typical approach used when defining networking protocols. While this is fine for general networking stuff, it should definitely NOT be used in crypto, and for security in general. This is because an attacker might use such precious information to build an attack to the system.
We will now see how to exploit such messages to decrypt a TLS packet.
1.3 The Attack
The attack we will now discuss works when you're using CBC with any block cipher. This means that you can use the strongest block cipher, like AES, and still be vulnerable to this attack. For this attack we'll assume a CCA attack model (Choosen Ciphertext Attack), which means that an attacker can forge an arbitrary cipher text, send it to the server, and see the response.
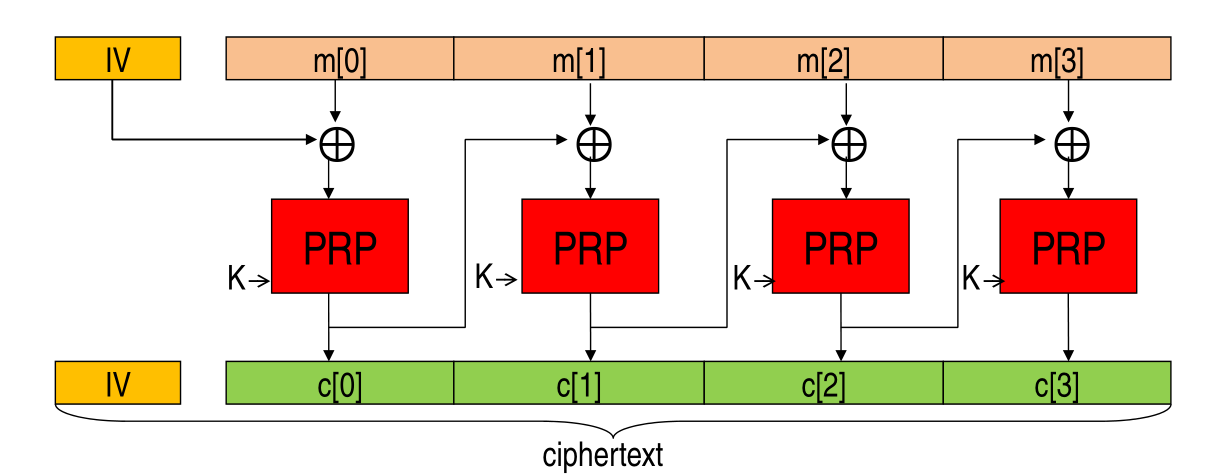
Before starting, let us remember how encryption is done with CBC.
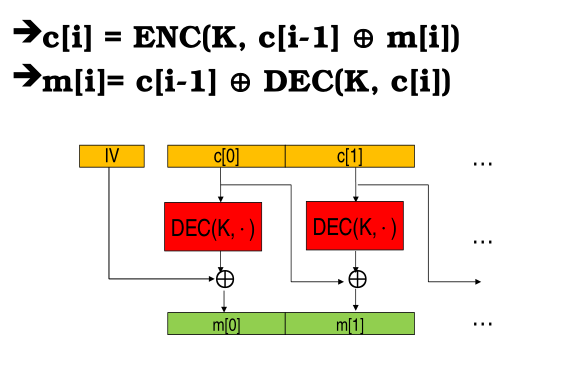
This means that decryption is done as follows
1.3.1 Second Block Onwards
To decrypt a block other than the first block the following attack can be used:
You sniff a proper message sent by someone else. Your objective is to break the second block of this message.
\[\text{IV} \,\, \Big| \,\, c[0] \,\, \Big| \,\, c[1] \,\, \Big| \,\, c[2] \,\, \Big| \,\, c[3] \ldots\]
You remove all blocks other than the first two.
\[\text{IV} \,\, \Big| \,\, c[0] \,\, \Big| \,\, c[1] \,\,\]
To understand if the last byte of \(m[1]\) is \(A\), you submit the following ciphertext, in which the last byte of \(c[0]\) is XOred with \(A \mathbin{\oplus} 0x00\).
\[\text{IV} \,\, \Big| \,\, c[0] \mathbin{\oplus} [ \ldots, A \mathbin{\oplus} 0x00] \,\, \Big| \,\, c[1]\]
At this point two things can happen, depending on how the server replies to you.
If the server replies with a bad_record_mac error message, then it means that the padding was correct, and thus your guess of \(A\) was right: the last byte of the proper \(m[1]\) was \(A\), which meanas that the last byte of the modified plaintext message was \(0\), which is a correct padding value, since \(m[1]\) is the last block of the message.
If the server replies with a decryption_failed error message, then the padding was not correct, and thus your guess of \(A\) was wrong: the last byte of \(m[1]\) was not \(A\). In this case you can try with another character, until you find the correct one.
To understand if the second last byte of \(m[1]\) is \(F\), you submit the following ciphertext, in which the two last bytes of \(c[0]\) are XOred respectively with \(F \mathbin{\oplus} 0x01\) and \(A \mathbin{\oplus} 0x01\).
\[\text{IV} \,\, \Big| \,\, c[0] \mathbin{\oplus} [ \ldots, F \mathbin{\oplus} 0x01, A \mathbin{\oplus} 0x01] \,\, \Big| \,\, c[1]\]
Once again, two things can happen, depending on how the server replies to you.
If the server replies with a bad_record_mac error message, then it means that the padding was correct, and thus your guess of \(FA\) was right: the second to last byte of the proper \(m[1]\) was \(F\), which meanas that the last two byte of the proper plaintext message were \(FA\), which means that the last two bytes of the modified plaintext message are \(0x1, 0x1\), which is a correct padding value, since \(m[1]\) is the last block of the message.
If the server replies with a decryption_failed error message, then the padding was not correct, and thus your guess of \(F\) was wrong: the second last byte of \(m[1]\) was not \(F\). In this case you can try with another character, until you find the correct one.
This is why this attack is called the oracle padding attack, because we are using the information about the correct padding to gain information about the original plaintext.
This attack is much, much faster than a simple brute-force attack, since assuming a block size of \(8\) bytes, the number of possible block values is \(256^8\), while in our attack we require \(256\) tries for each byte of the block, requiring at most \(256 \cdot 8 = 2^{11} = 2048\) tries.
Q: assume a CBC-based block encryption scheme which uses block sizes of \(4\) bytes each. Assume that the attacker sees the following ciphertext (hex notation)
f1 aa 11 04 | 34 35 f1 20 || 11 01 9c 01 || ac c3 83 02 || 91 11 5f 10
Assume now that the server is vulnerable to a Padding Oracle attack. The goal of the attacker is to check whether the plaintext corresponding to the 16th byte (the byte whose ciphertext is 02) is the byte
0x0f hex = 00001111 binary
Which Choosen ciphertext message should the attacker send to the server/oracle, and why?
R: The attacker should send the following ciphertext message
f1 aa 11 04 | 34 35 f1 20 || 11 01 9c 0e || ac c3 83 02
Where the only byte we changed is the 16th byte, and we transformed it from 01 to
0x01 XOR 0x0f = 0000 0001 XOR 0000 1111 = 0000 1110 = 0x0e
Like this if the 16th byte of the plaintext is actually 0x0f, then after the decryption the resulting plaintext would be 0x00, which is a correct padding value, which means we would get a bad_record_mac from the server. If we instead get decryption_failed then the padding was not correctly set up and thus our guess was wrong.
2 Is the Attack Pratical
Notice that in a single connection you can only send a single message to the server before the connection breaks, and after that the new connection will have a different key. This means that it seems impossible to actually execute such an attack in a pratical sense.
Well, this consideration turned out to be wrong, because in 2003 Vuagnoux and Canvel managed to implement such an attack on the IMAP protocol, in which client periodically sends login/password every few mins (from 1 to 5). Even though every new connection uses a different key, the plaintext message is the same and is formatted in the same way. This means that every 1 to 5 mins they were able to make a single guess on one byte of the password. By optimizing the attack with some dictionary help, they showed that such an attack could be done in a matter of a few hours.
3 Fixes and Follow-Ups
The main problem was that TLS v1.0 standardized two messages, (bad_record_mac), (decryption_failed). This attack was discovered in 2002 by Vaudenay, and most implementations of TLS added a patch in which the server responded with the same alert (bad_record_mac) in both cases). Finally TLS v1.1 standardized this merging of alert messages.
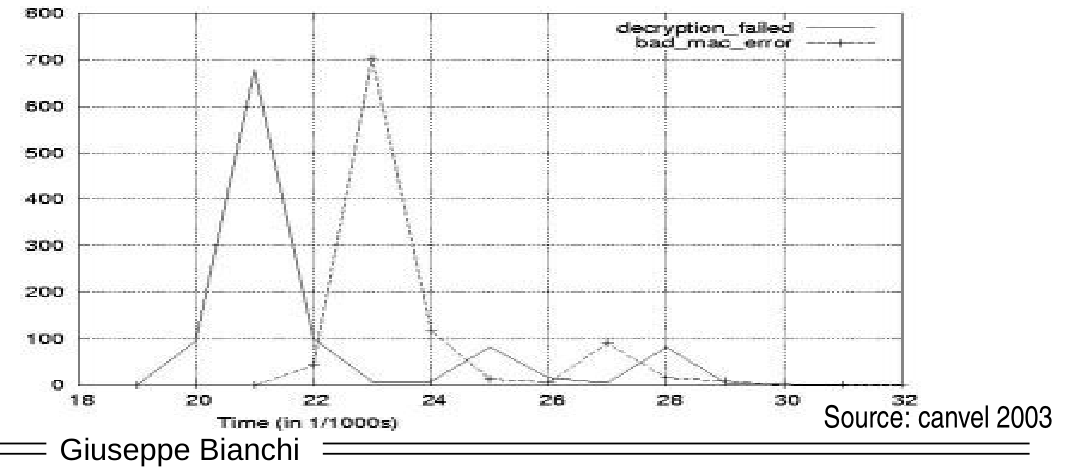
This however was not the end of the story. Indeed, for in 2003 canvel discovered another attack, named side channel padding oralce, which exploited the time that the server took to respond to understand if the padding was correct or not. The attack was based on the fact that if the padding was correct, then the server would perform the MAC computation, and only then reply to the client, while if the padding was not correct, the server would immediately reply to the client. This introduced a side channel, in which informations about the plaintext was leaked through the time spent to reply to the client.
Ideally to fix this problem you would need to write a program in which all checks were made, and which guaranteed that whether ot not the padding was correct, the response timing would be the same. An example of equal time programming code is the following
flag = 1 if (first_check) then flag = 0 if (second_check) then flag = 0 if(flag == 0) return BAD_MAC
To actually have these guarantess you have to forget optimizers, since they usually optimize performance, and not security. In TLS this was fixed in TLS v1.2, in which the MAC was validated regardless if the padding failed or not.
Notice however that if the padding fails, there is no way to know where the message ends and the padding begins. This creates a problem: how much data should be included in the HMAC computation? In TLS v1.2 the solutionn adopted was to use the whole data for validation. Notice that this is more data than a correct message. In 2013, kanny Paterson came out with an attack called Lucky thirteen, which basically measured the time needed to compute an extra HMAC block.
The story however doesn't end here, and in the following years other attacks would be implemented, all which exploited the fact that in the original version of TLS you first decrypt and then check the MAC:
In 2014 there was an attack named PODDLE, which combines a padding oracle with an SSL 3.0 downgrade.
In 2015 there was Lucky microseconds, by Albrecht and Paterson which uses a very subtle timing channel.
Then in 2016 There was LuckyNegative20, by Filippo Valsorda.
4 Lessons Learned
From this discussion of the padding oracle attack we can extract the following wisodm:
If in TLS v1.0 it was decided to ENCRYPT and then MAC, just like IPsec does, all of these attacks would've been avoided, since by choosing a strong MAC, the attacker could not do a Choosen Plaintext Attack (CPA). Since you can't now change the order of operation, starting from TLS v1.3 AEAD became mandatory.
When dealing with cryptography, and security in general, you need to be very careful with your error messages. The least, the better, because when you differentiate an answer, there might be an oracle lying behind your answers.
Crypto implementations are extremely critical. Be aware of side channel attacks, don't implement crypto yourself, and just use standard cryptographic libraries such as:
Openssl
Libsodium
Bouncycastle
The cryptographer Moxie Marlinspike, which developed the security of WhatsApp before moving to Signal (when WhatsApp was bought by facebook), developed the so-called Cryptographic Doom Principle, which says
If you have to perform any cryptographic operation before verifying the MAC on a message you've received, it will somehow inevitably lead to doom.