CNS - 19 - Block Ciphers
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides:
Introduction: In this lecture we will discuss about how block ciphers work and how they are used.
1 Block Ciphers
In the first lectures of the course we discuss about substitution ciphers, which can be thought of as mappings from letters to letters such as
\[\begin{split} A &\longleftrightarrow F \\ B &\longleftrightarrow H \\ C &\longleftrightarrow X \\ D &\longleftrightarrow A \\ \end{split}\]
Block ciphers are a generalization of this approach, in which we have a plaintext block of \(n\) bytes which is transformed in a ciphertext block of \(n\) bytes.
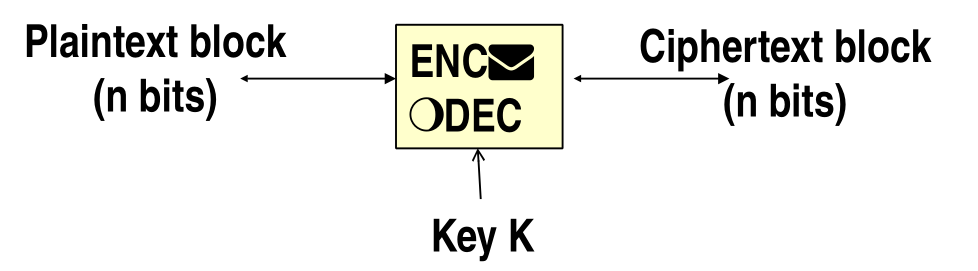
The type of transformation is driven by the secret key \(K\), which selects one particular transformation among all the possible permutations. In theory the block algorithm should implement a Pseudo Random Permutation (PRP); in pratice the key permits to select "only" a subset of the possible permutation, which in particulare are \(2^{\text{textsize}}\).
1.1 Pseudo Random Permutation
Let \(n = 3\), and consider the set \(S\) of all the possible plaintexts. We have that \(|S| = 2^n = 2^3 = 8\), and in particular
\[S = \{000, 001, 010, 011, 100, 101, 110, 111\}\]
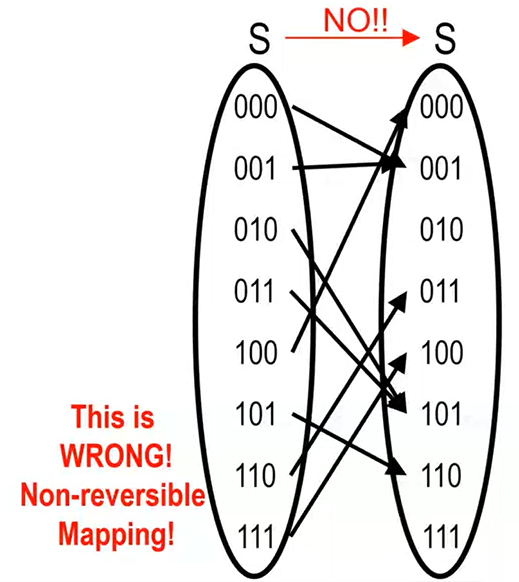
A permutation is a bijective function \(\Pi: S \to S\), which maps every element of \(S\) to another element of \(S\) such that no element of \(S\) are mapped to the same element of \(S\). Graphically we get,
\[\begin{split} 000 &\longleftrightarrow 000 \\ 001 &\longleftrightarrow 001 \\ 010 &\longleftrightarrow 010 \\ 011 &\longleftrightarrow 011 \\ 100 &\longleftrightarrow 100 \\ 101 &\longleftrightarrow 101 \\ 110 &\longleftrightarrow 110 \\ 111 &\longleftrightarrow 111 \\ \end{split}\]
Remember that the transformation \(\Pi\) must be reversible, meaning that the function has to be a bijection. An example of a wrong transformation is the following one, since multiple elements are mapped to the same one.
A pseudo random permutation then means that with the same probability we select one of the possible permutation of our set of elements. That is, the probability is uniformly distributed among all possible permutations. By fixing the key \(k\) we fix a particular permutation. Ideally thus we'd like to have a key value for every single permutation.
Now, here comes the problem of this approach: consider the number of permutation of a set of \(n\) elements. This number is \(2^n!\) This number gets incredibly large incredibly soon, as the following examples show
If \(n = 3\), then \(2^3! = 8! = 40320\)
If \(n = 8\), then \(2^8! = 256! = 2.58 \times 10^{506}\)
In AES, \(n = 128\), which means that \(2^{128}! = 2^{2^{135}}\), which is an unbeliveable large number.
Notice that if we want to have a key for every possible permutation, in the case of AES we'd need a \(10^{40}\) digits key. In actuality AES keys have \(128\), \(192\) and \(256\) bits, which only allow to select a "small" fraction of the total number of permutations.
This means that in principle the limited length of our keys allow us to only select a fraction of the total number of permutations. So even if with a strong block ciphers we're still far from an idealized version of a PRP.
1.2 Stirling Approximation
To actually compute factorial values the following approximation, called Stirling Approximation, can be used
\[n! \approx \sqrt{2 \pi n} \frac{n^n}{e^n}\]
We can use such approximation to compute, for example, the total number of permutation in AES
\[\begin{split} 2^{128}! &\approx \sqrt{2\pi2^{128}} \cdot \frac{2^{128 \cdot 2^{128}}}{e^{2^{128}}} \\ &\approx \sqrt{2\pi} 2^{64 + 2^{135} - 2^{128} \cdot \log_2{e}} \\ &\approx 2^{2^{135}} \\ \end{split}\]
2 Possible Problems
In our discussion of block ciphers we will not analyze in depth how these pseudo random permutations indexed by a key value \(k\) are defined. We will simply assume that they exist, and we will analyze how to use them.
2.1 Problem 1: Plaintext Longer than Block Size
When the plaintext is longer than the block size we need to do something about it.
2.1.1 Electronic Code Book
The first (bad) idea is to simply split the message into \(n\) bit chunks, and apply the PRP to each block to get the relative cipher blocks. This is called the Electronic Code Book (ECB mode), and its characterized by the fact that each block is encrypted indipendently.
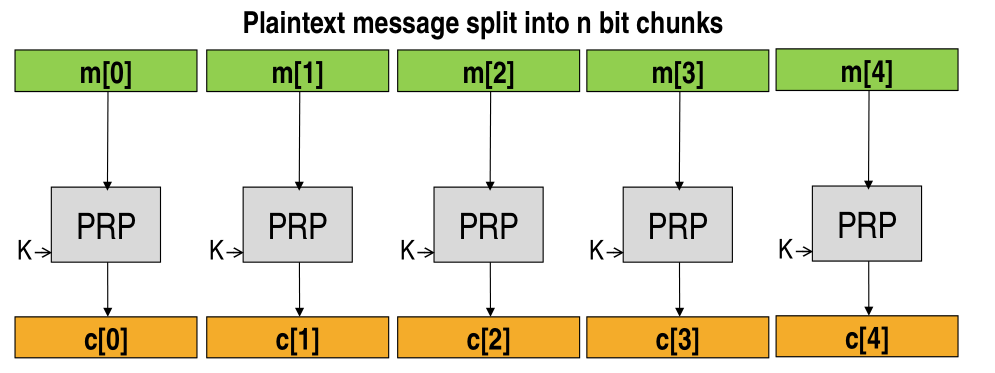
The problem with this approach is that you lose semantic security, since if two blocks contain the same plaintext message, then also the relative cipher blocks will be the same (since the key \(k\) used is also the same).
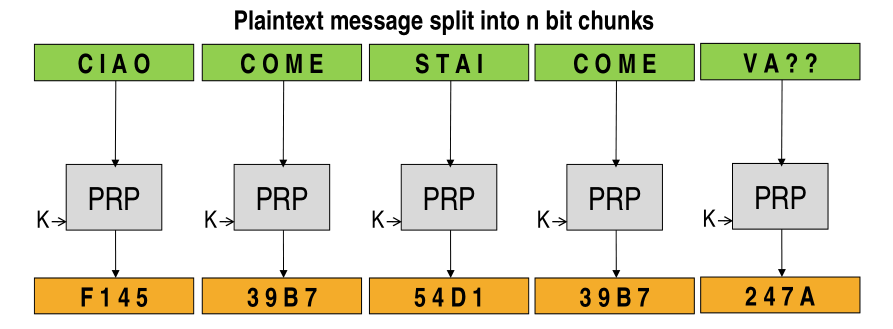
This is why you should never, ever use ECB.
2.2 Problem 2: Encrypt same message twice?
Another problem when using block ciphers is to deal with the situations in which the same message in encrypted twice.
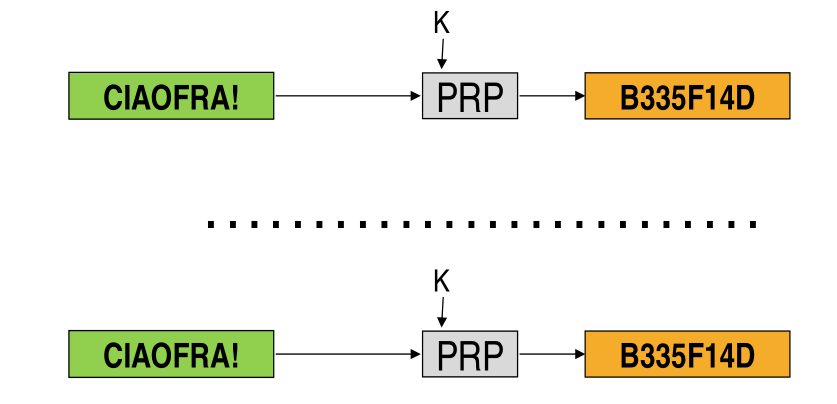
Notice that if we don't do anything, we once again lose semantic security.
2.2.1 IVs in Block Ciphers
To fix this problem the idea is to use Initialization Vectors (IVs). In particular we want to generate a fresh IV for every new encryption. Once we have generated an IV we can use it as follows
First we encrypt

Then we transmit

Finally we decrypt
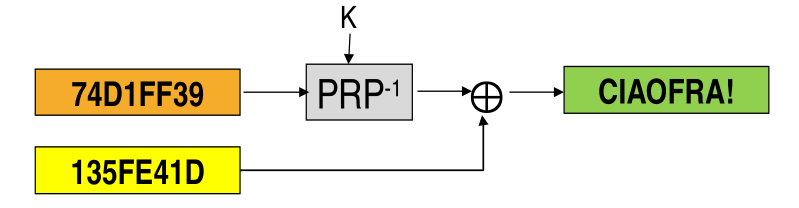
Notice that we already know that IVs should never repeat, since otherwise we'd lose semantic security. Very few people know however that in this specifici application the IVs should also be unpredictable. The BEAST attack done in 2011 to TLS used the predictability of IVs to attack the system.
3 Modes of Operation
A block cipher has two ingredients:
The block cipher itself.
The mode of operation, that is the way to combine the various blocks. By specifying a proper mode of operation we are able to encrypt messages of arbitrary size.
There are many modes of operations

For standard encryption the most used modes are:
Cipher Block Chaining (CBC)
Counter Mode (CTR)
The NIST recommended (in 2001) the following two modes:
CBC
CTR
Cipher Feedback Mode (CFB)
Output Feedback Mode (OFB)
Finally, there other modes which offer more advanced properties like authenticated encryption schemes (AEAD) such as:
Galois Conter Mode (GCM)
Offset Codebook Mode (OCB)
3.1 Guarantee Semantic Security
In principle to guarantee semantic security we just have to split our message into \(n\) blocks, generate for each block and IV, and use the PRP on each block with the key \(k\) and the generated IV.
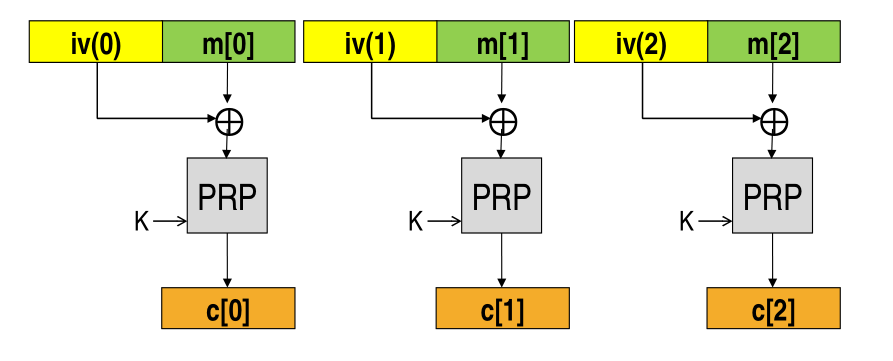
The problem with this approach is that if the IVs are randomly generated, then we'd need to include for each block the relative IV block, and we would thus double the size of the message to be transmitted. This approach is thus not practical.
We thus have to find other means to do this.
3.2 Cipher Block Chaining (CBC)
The Cipher Block Chaining is based on the idea that each ciphertext block can be used as a sort of IV for the next plaintext block.
With CBC the encryption works as follows
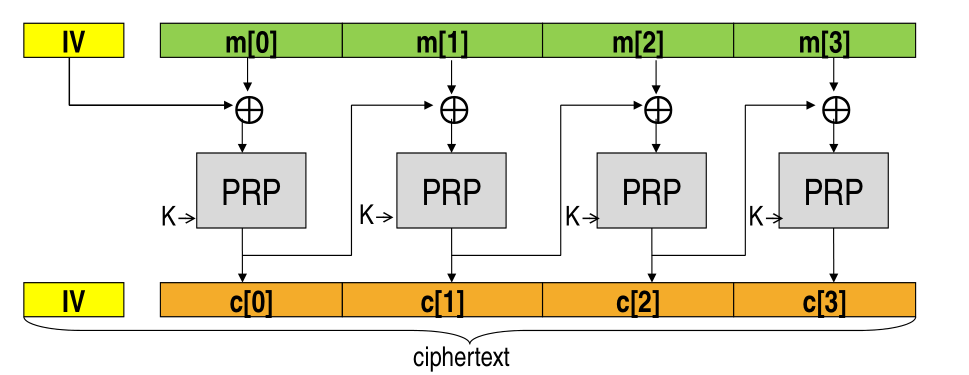
In formula,
\[\begin{split} c[0] &= \text{ENC}(k, IV \mathbin{\oplus} m[0]) \\ c[i] &= \text{ENC}(k, c[i-1] \mathbin{\oplus} m[i]) \\ \end{split}\]
The overhead of transmission is just \(1\) block, since at the end we only have to add the first IV vector. The decryption of CBC instead works as follows
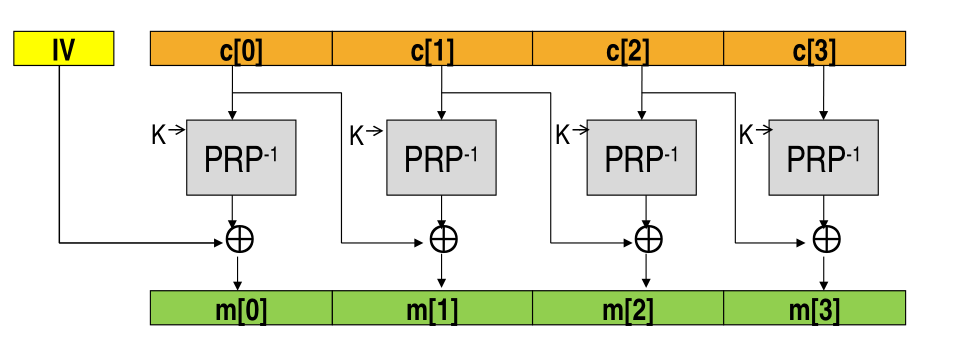
Notice that while the encryption is not parallelizable, the decryption can be parallelized, which makes it a much faster to decrypt.
About CBC the following things can be said:
It is widely used and secure, but its security depends on the assumption that the nonce is random and non predictable.
It is slow during encryption, which means that it is not appropriate for very high performance scenarios.
Encryption and decryption require two different circuits. This could be a problem in the hardware.
The plaintext must be multiple of block size, and padding can be used to fill the space (for example TLS padding uses the standard PKCS#7).
Q: Consider a block cipher of 3-bit blocks which uses the following permutation
\[\begin{split} 000 &\longleftrightarrow 001 \\ 001 &\longleftrightarrow 010 \\ 010 &\longleftrightarrow 111 \\ 011 &\longleftrightarrow 101 \\ 100 &\longleftrightarrow 000 \\ 101 &\longleftrightarrow 110 \\ 110 &\longleftrightarrow 011 \\ 111 &\longleftrightarrow 100 \\ \end{split}\]
and the following message \(M = 001 \,\, 001 \,\, 001\). Encrypt \(M\) first using ECB, and then using CBC with an IV of \(010\)
A: When we encrypt \(M\) with ECB we get
For the first block we get \(001 \to 101\)
For the second block we get \(001 \to 101\)
For the first block we get \(001 \to 101\)
Thus we get the following ciphertext
\[C_1 = 101 \,\, 101 \,\, 101\]
When instead we encrypt \(M\) with CBC we get
For the first block we get
\[001 \mathbin{\oplus} 010 = 011 \to 101\]
For the second block we get
\[001 \mathbin{\oplus} 101 = 100 \to 000\]
For the third block we get
\[001 \mathbin{\oplus} 000 = 001 \to 010\]
Thus we get the following ciphertext
\[C_2 = 101 \,\, 000 \,\, 010\]
3.3 Cipher Feedback Mode (CFB)
This mode should not be studied for the course, but it is useful to understand even a little bit how it works.
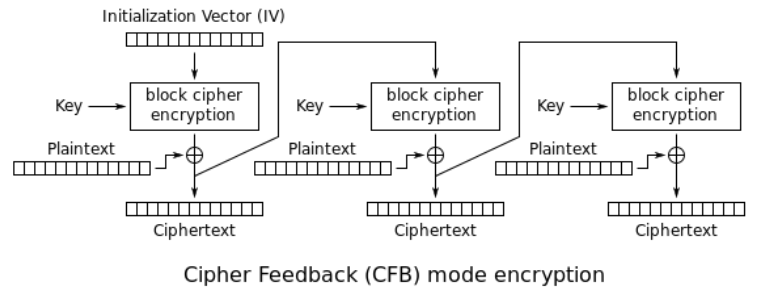
In CFB the IV is passed to the block to get a sort of keystream, which can then be XORed with the plaintext. This is akin of transforming a block cipher into a sort of stream cipher.
Decryption in CFB works as follows
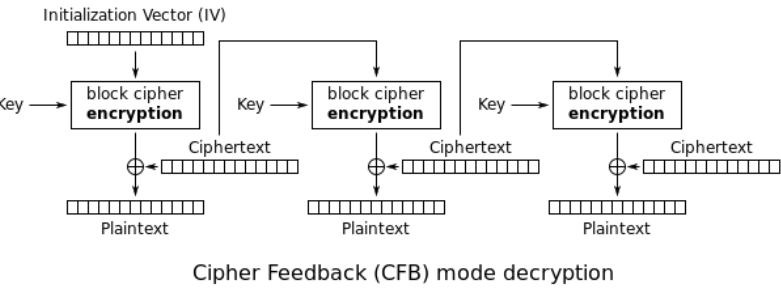
Notice how in this case we don't need to implement two different circuits for encryption and decryption: since encryption is actually done with XOR, as long as we can construct the keystream used, we are able to decrypt all blocks.
3.4 Output Feedback Mode (OFB)
OFB works very much like CFB, with a slight but significant difference.
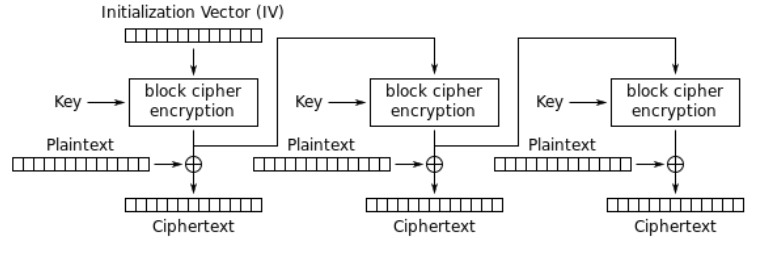
Notice that in OFB the stream generated for the second block onwards is not the output of the keystream XORed with the first plaintext, but is rather the keystream itself. This makes a huge difference, since it means that in OFB you can pre-process all the keystrams required. In this sense OFB is very much like a stream cipher that depends only on the initialization vector IV.
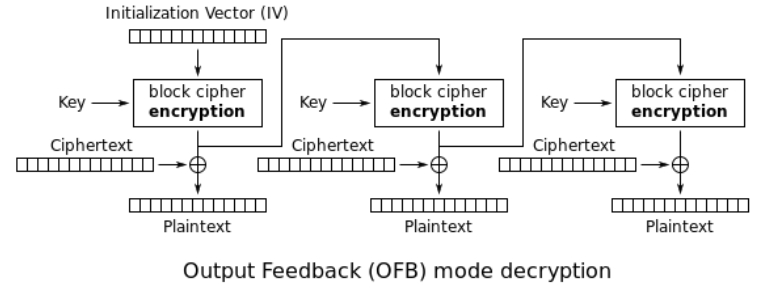
Notice that also in CFB, as it was in CFB, we dont need two implement two different circuits for encryption and decryption. As a second advantage, in CFB we can also do parallel decryption, since we can generate all keystreams in parallel.
3.5 Short Cycle Problem
Notice that in modes like OFB, the keystrams are generated by applying again and again the PRP with the same key \(k\).
\[\text{IV} \to \text{PRP} \to \text{PRP} \to \text{PRP} \to \ldots\]
Notice however that not all permutations are the same. In particular some permutation lead to the so-called short cycle, meaning that the periodicity in your permutation is much smaller than the maximum periodicity possible.
For example, consider the following permutation
\[\begin{split} 000 &\longleftrightarrow 001 \\ 001 &\longleftrightarrow 010 \\ 010 &\longleftrightarrow 111 \\ 011 &\longleftrightarrow 101 \\ 100 &\longleftrightarrow 000 \\ 101 &\longleftrightarrow 110 \\ 110 &\longleftrightarrow 011 \\ 111 &\longleftrightarrow 100 \\ \end{split}\]
Then, if we consider an OFB keystream generated with \(\text{IV} = 010\) we get the following
\[010 \to 111 \to 100 \to 000 \to 001 \to 010 \to 111\]
thus we have a cycle of length \(5\). If instead we have \(\text{IV} = 011\) we get the following
\[011 \to 101 \to 110 \to 011 \to 101 \to 110 \to 011\]
thus we have a cycle of length \(3\).
This means that the security of the system depends both on the IV and on the key used. Another way to say this is that the security depends on the specifics of the black box that is the PRP and on its cyclic properties. This problem affects the following modes of operations:
CBC
CFB
OFB
Observation: The problem of short cycles is also present in hash chains. This is why crypto guys typically hate "chaining" stuff.
3.6 Counter Mode (CTR)
The counter mode encryption solves the short cycle problem, and it works as follows: we have a counter and we increase it by one for every new block. We then apply the non linear permutation to the counter to obtain a keystream, which we XOR it to the plaintext to get the final ciphertext.
The encryption thus works as follows
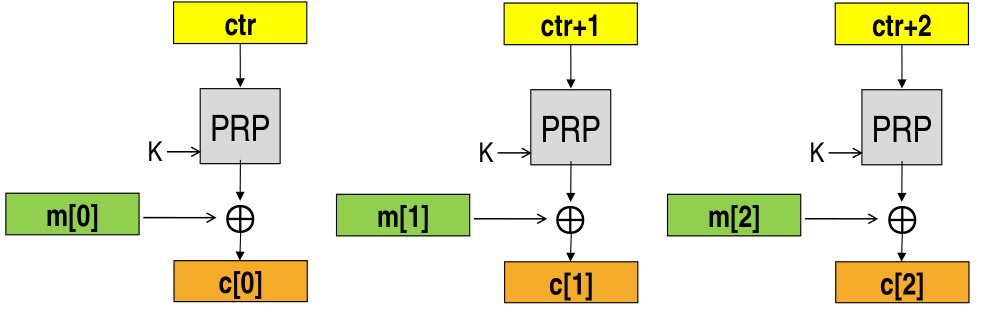
In pratice CTR builds a PRNG keystream using a block PRP. Notice however that like this we have not mentioned the IV, which is still needed if we want to encrypt the same message and we start with the same counter value. To deal with this problem it was standardized (RFC3686) that if you accept that your maximum size for encryption is \(2^{32}\) blocks, then you take the last \(32\) bits of the counter and you use them as an actual counter, while the first \(128\) bits of the counter are used as an IV.
If PRP is secure then we can prove that the PRNG generated is secure as well.
CTR modes offer the following advantages:
Both encryption and decryption are parallelizable.
It requires the implementation of a single circuit
It offers random access
It guarantees no short cycles.