CNS - 22 - Asymmetric Cryptography I
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides:
Introduction: In this lecture we started talking more in depth about asymmetric cryptography.
1 Asymmetric Cryptography
The general scheme to have in mind for asymmetric cryptography is the following one
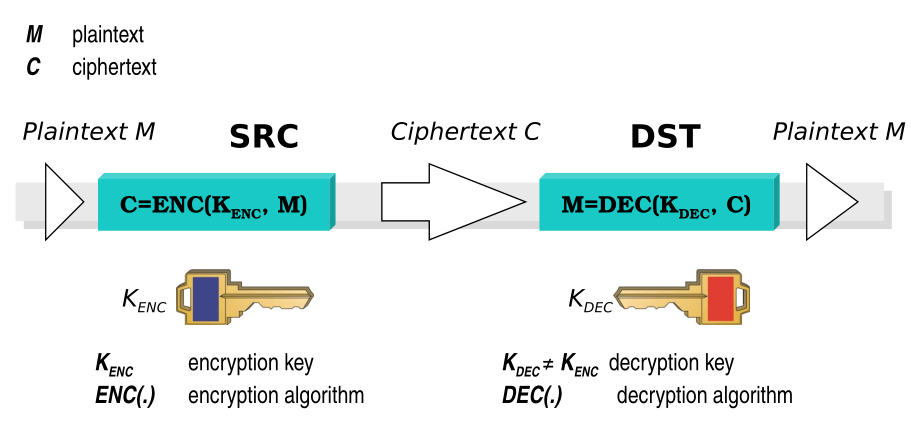
As we can see, the main difference from the standard paradigm of symmetric cryptography is that in asymmetric crypto we have two different keys: an encryption key and a decryption key.
The encryption key is also called the public key since it is made public, while the decryption key is also called the private key, since it it usually kept private. With this approach everyone can encrypt, but only the owner of the private key can decrypt what was encrypted with the publci key.
2 Practical usage
Let us see now some pratical usage of asymmetric crypto
2.1 HTTPS/TLS-Style
In this model the asymmetric crypto is used to set up a shared secret between the client and the server. This shared secret is then used to derive the symmetric key for encryption and message authentication using soem key derivation function (KDF).
This model has mainly three phases:
handshake
data transfer
rekeying + data transfer
2.2 Hybrid Encryption
Suppose now you don't want to set up a TLS connection, but you still want to encrypt your email using public key crypto so that only giuseppe bianchi can read it later on. To do so a hybrid encryption scheme is used. Such a scheme can be visualzied as follows:
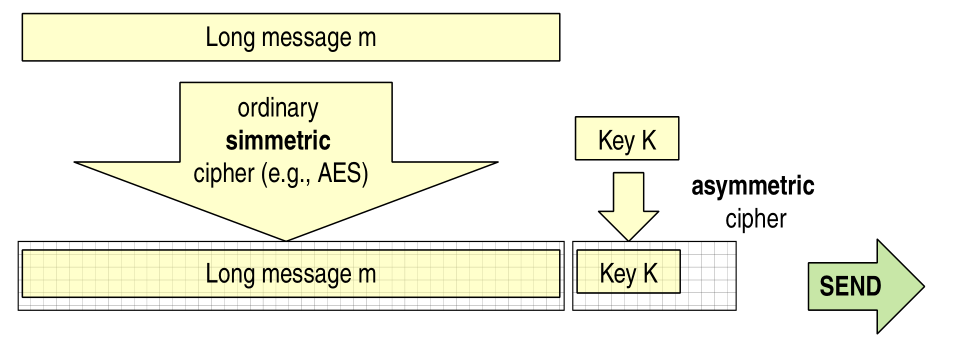
In detail:
Generate a (random) symmetric key \(k\)
Use key \(k\) and symmetric cipher to encrypt (long data)
Encrypt \(k\) with asymmetric encryption using the public key of giuseppe bianchi, and send it along the message.
Observation: In 5G they introduced a way to avoid the need to transfer your identity in the network. In order to do this asymmetric crypto is used, and more in particular they use ECIES (Elliptic Curves Integrated Encryption Scheme). For more information see 5G SUCI.
2.3 Two Ways to Use It
There are two way of using asymmetric encryption:
Public key encryption: In this scheme the public key is used to encrypt the data, and it can be used by anyone, while the private key is used to decrypt the data, and it can be used only by the owner of the data.

Digital signature: In this opposite scheme the private key is used to encrypt the data, while the public key is used to decrypt the data. This works as long as the operation of encrypting and decrypting are commutative. This approach can be used to guarantee that the one who encrypted the data is the owner of the private key and it can thus be used as a message authentication (integrity) mechanism.
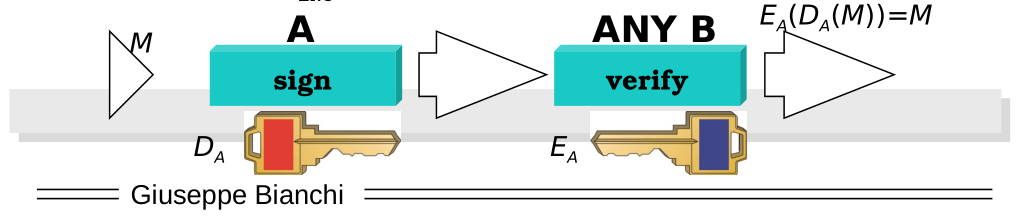
2.3.1 Digital Signature
Digital signtature is used to ensure integrity as well as source authentication when no shared key can be exchanged. It can be implemented using asymmetric crypto as follows:
The sender has to do the following steps:
You add to the message \(m\) to be sent a tag computed using a cryptographic hash function \(H(m)\).
Encrypt the tag with our own private key.
Send the message.

When the receiver gets the message, the following steps can be done to check the integrity of the message as well as the source of origin:
You get the public key of the sender of the message and you used it to decrypt the tag of the message.
You compute the hash of the message and check if the tag matches. If it does, then the message is valid, otherwise it isn't.
Notice how the hash added at the end of the message has two, distinct goals:
To shorten the message such that you can apply the transformation to a single block.
For security. This means that even if you have a small message like \(M = 20\) bits, you should still hash it, for otherwise you get a problem called malleability, which will be discussed later on.
With this approach we get the non-repudiation property, because only the owner of the private key can send the correct tag.
3 The Pioneers
In the 1970s there was only symmetric encryption, and the crypto community started to wonder if there were ways to send encryption keys from one place to another securily.
In 1976 Diffie and Hellman started the basis for asymmetric cryptography by introducing the diffie-hellman key agreement, which is the first asymemtric algorithm used in crypto.

Then, in 1977, the first ever public key encryption and digital signtature, the RSA crypto system, was found.

To complete the story, in 1965 El Gamal found an asymemtric encryption scheme which used the same principles as teh diffie-hellman exchange.
4 Asymmetric Problems
The basic ingredient for an asymmetric encryption scheme is to find an asymmetric, hard problem, that is a problem that is computationall easy in one direction, but computationally hard to solve in the opposite direction.
Some asymmetric problems are:
The discrete logarithm problem in prime fields \(\mathbb{F}_p\) was used to diffie-hellman for their key agreement protocol. The problem is described as follows:
Forward direction (easy): Given large prime \(p, g, x\), compute
\[y = g^x \mod p\]
Backward direction (hard): Given \(y = g^x \mod p\), compute
\[x = \text{DLog}_g(y) \mod p\]
The factoring problem of factoring a product of two large prime was instead used to build the first asymmetric crypto system RSA. The problem is described as follows:
Foward direction (easy): Given \(p\) and \(q\) large primes, compute
\[N = p \cdot q\]
Backward direction (hard): Given \(N\), find factors \(q, p\).
4.1 Modular Exponentiation (is easy)
Let \(p\) be a prime, \(g\) be a generator. Then, given a number \(x\), we want to compute \(g^x \mod p\). Notice that this can be done easily in polynomial time with the following algorithm

In general if we have an \(n\) bit number, the complexity of the operation is \(O(n^2)\) moltiplications and \(O(n/2)\) additions.
4.1.1 Example
For example, if we want to compute \(g^{1437}\), we can do the following
First we express \(1437\) in binary to obtain
\[(1437)_{10} = (10110011101)_{2}\]
Then we start the so-called square-multiply algorithm and construct the following table, where the the first row is obtained by reading the bits of the number from the least significant bit (lsb) to the most significant bit (msb)
\[\begin{array}{c | c | c2} \text{Bits} & \text{Square} & \text{Multiply}\\ \hline 1 & g & g \\ 0 & g^2 & g \\ 1 & g^4 & g \cdot g^4 = g^5 \\ 1 & g^8 & g^5 \cdot g^8 = g^{13} \\ 1 & g^{16} & g^{13} \cdot g^{16} = g^{29} \\ 0 & g^{32} & g^{29} \\ 0 & g^{64} & g^{29} \\ 1 & g^{128} & g^{29} \cdot g^{128} = g^{157} \\ 1 & g^{256} & g^{157} \cdot g^{257} = g^{413} \\ 0 & g^{512} & g^{413} \\ 1 & g^{1024} & g^{413} \cdot g^{1024} = g^{1437} \\ \end{array}\]
Notice that to compute the final result we only needed \(16\) operations instead of \(1436\) operations.
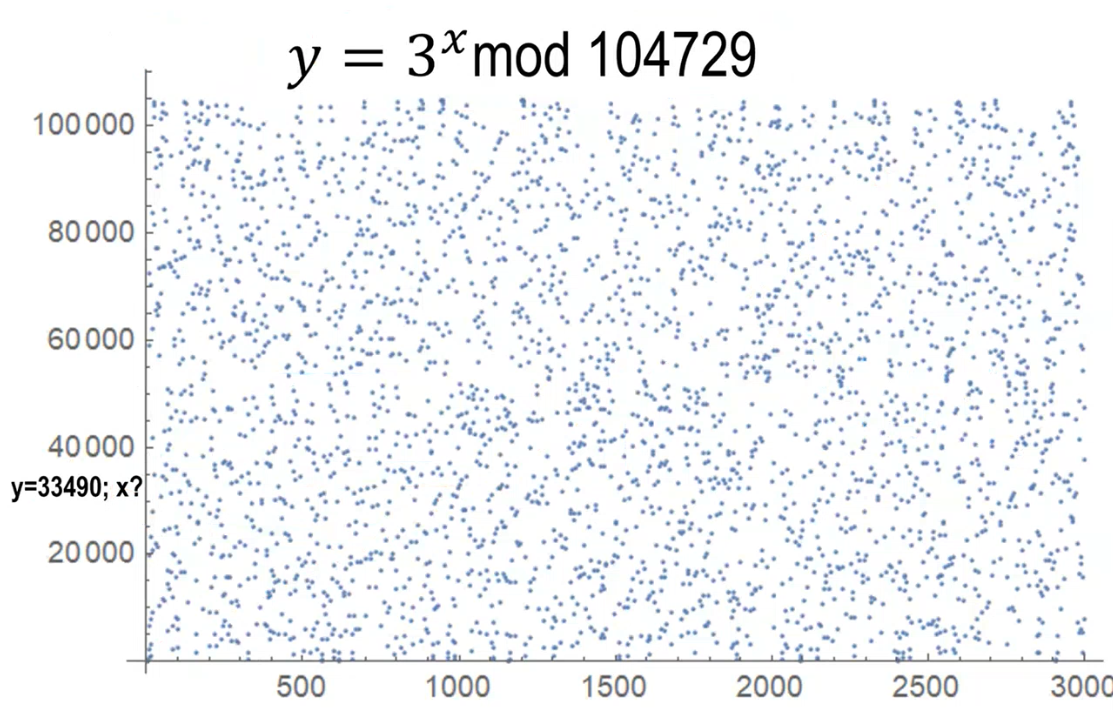
4.2 Discrete Logarithm (is hard)
Suppose you have \(y = 3^x \mod 104729\). Then its really hard to find the value of \(x\) given the value of \(y\). Indeed, if we plot this function we get the following
5 Diffie-Hellman Key Agreement
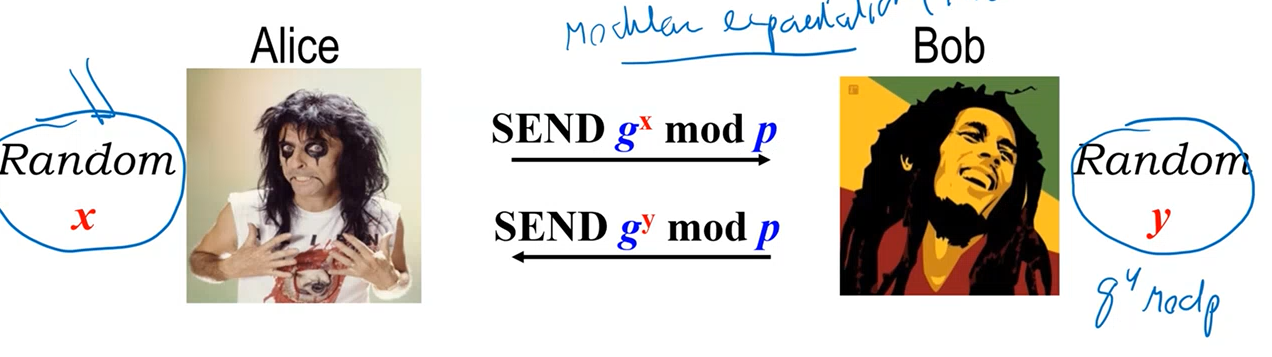
The Diffie-Hellam protocol was developed in 1976 and it symbolizes the invention of asymmetric cryptography, although it did not solve the public key cryptosystem problem, which was later solved by RSA in 1977. The DH protocool is a key agreement protocol, meaning that it allows to securily setup a shared secret at both ends, by only exchanging public values without having a secure channel.
The protocol work as follows:
You have two people, Alice and Bob. Both of them at the start generate a random quantity.

Alice then sends to Bob the value \(g^x \mod p\)

Bob instead sends to Alice \(g^y \mod p\)
Both Alice and Bob then raise the number they receive to the power using their secret number.
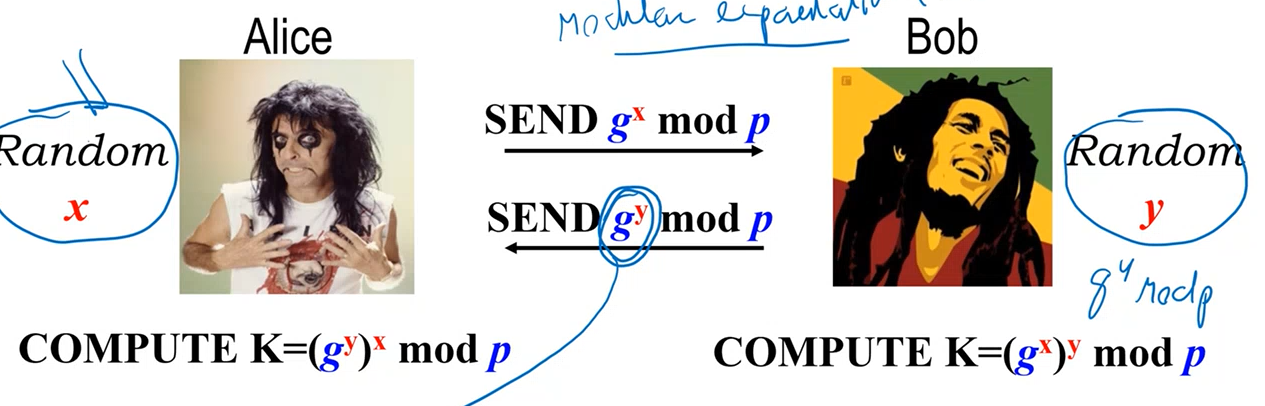
Notice that if an attacker wants to compute the secret key he has to solve the discrete logarithm problem, which is hard to solve.
5.1 DH Functional Limitation
Even DH solves the problem of sharing a key, it does not by itself implement a public key cryptosystem. That is, you cannot transfer data encrypted with DH.
From DH is not immediate to derive a digital signature scheme.