CNS - 24 - Asymmetric Cryptography III
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides:
Introduction: In this lecture we continued our discussion with asymmetric cryptography by talking about digital certificates and more generally about the public key infrastructure needed to ensure the security of asymmetric crypto.
1 The Problem with Public Keys
Remember that using an asymmetric crypto system like RSA we can offer the digital signature by appending to the message the hash of the message encrypted with out private key.

If the receiver wants to understand whether or not the message is valid, i.e. the message was sent by the real user, he can simply get the public key of the user and use it to decrypt the hash of the message, compute the hash of the message once again and compare the two results to check if they are equal.
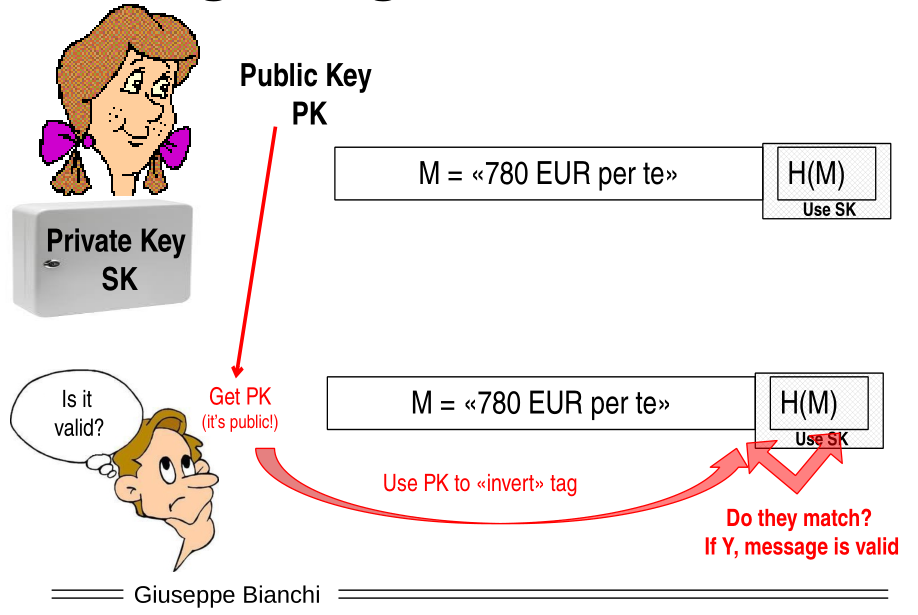
A possible way to break this system is the following: an attacker generates a private and public key of his own, and signs a modified version of the original message with his own private key. When the receiver tries to verifies the signature, the attacker then pretends to be Flavia and instead of sending to him the actual public key of Flavia, he sends to the victim his own public key.

Unless the receiver has somewhere stored all the valid public keys, he will have to ask for the public key of the sender of the message, and therefore this attack is doable.
The problem we have just shown for digital signature in reality affects various other contexts, such as:
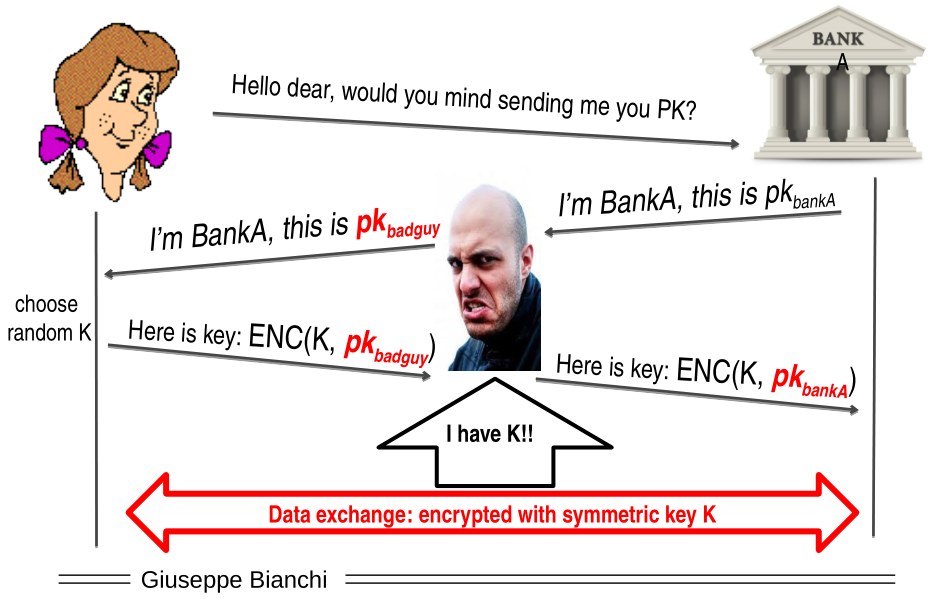
RSA key transport: This protocol is vulnerable to a MITM attack in which an attacker modifies the public key received by the end user.
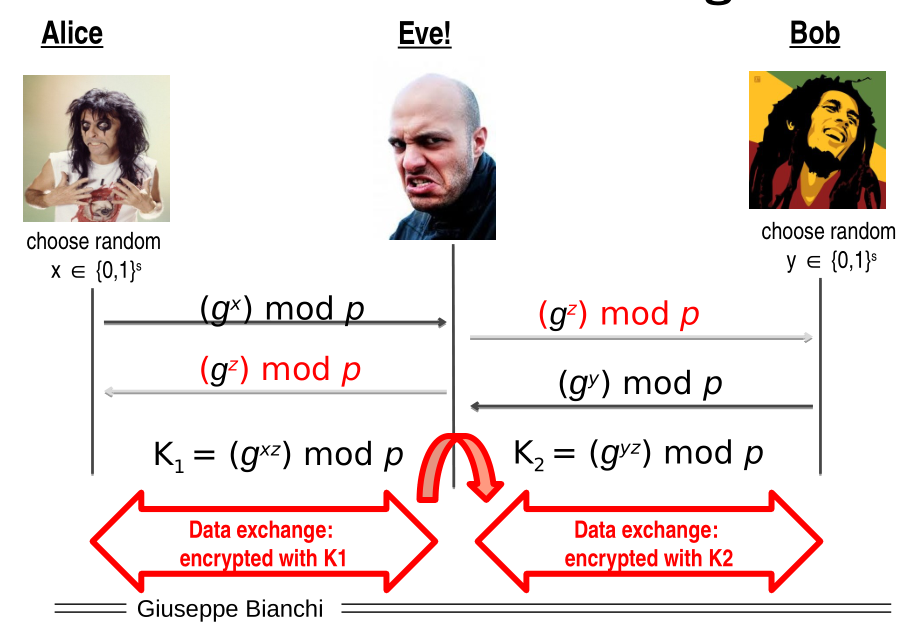
Diffie-Hellman key agreement: This protocol is also vulnerable to MITM attack.
All of these different attacks can be avoided if we are able to cryptographically bind a public key to an identity.

To solve this problem we need to introduce the concept of a digital certificate.
2 Digital Certificates
A digital certificate is something that permits me something to bind a public key to a subject, which can be a person, a company , a legal entity and so on.

Now, how are we able to create such certificates, and how can we ensure that they actually work like they are supposed to? This problem cannot be solved by mathematics alone. The only solution for this problem relies on trusting a third party, called a certification authority, which job is to make sure that certificate do what they are supposed to do.
Notice that we cannot ask online the certificate authority if a certain entity has a certain public key, for otherwise we'd still be open to MITM attacks. This certification has to be tighly integrated in the data. In particular the idea is to ask the certificate authority offline to sign a certificate which contains both the subject name and the subject public key. Such certificate represents the cryptographic bind we were looking for, and we trust this certificate as long as it is cryptographically by the certificate authority.
Notice that the security offered by this solution relies on the assumption that we can trust the certificate authorities. This doesn't seem optimal, however nothing better than this can be obtained.
2.1 Iussing a Certificate
Let's suppose we are a bank and we want to associate our identity with a specific public key. The process of issuing a new certificate has to be done exclusively offline. It works as follow.
The bank generates a new pair of private \((S_k)\) and public key \((P_k)\) using an asymmetric crypto system such as RSA.
The bank stores locally the secret key, to keep it secret.
A guy from the bank goes to the certificate authority (CA) and gives to the CA the identity of the bank and the public key of the bank. This has to be done offline, or in general using a secure channel.
The bank generates a new certificate, which is signed using the private key of the certificate authority.
\[\text{CERT} = (\text{BankName}, \text{BankP}_k)_{\text{CA_sign}}\]
The bank then sends the certificate to the bank.
Notice that in this workflow there are at work two pairs of private/public key: the pair of the bank, and the pair of the CA.
2.2 Verifying Certificate Validity
Suppose now that we are a client of the bank, and we want to ensure that the bank has really the public key it claims to have. The process of verifying the validity of a certificate works as follows
In the handshake process the bank sends the client the certificate previoulsy obtained by the CA.
As long as the user trusts the certificate authority that signed the certificate, the user can check the validity of the certificate.
If the CA signature is OK, then I'm sure that the bank really has that public key.
Finally, the client asks the bank to prove the possesion of the private key of the bank \(S_k\) associated to the public key contained in the cert. This can be done in two ways, either by asking the bank to sign something fresh (to avoid replay attacks), or by asking the bank to decrypt something fresh.
In order to validate the CA signature I need the public key of the CA, which has to be preinstalled in the PC. Now, since we don't handle raw public key but always use certificate, the public key of the CA must be within a certificate. Ok but then, who signs the certificate that maps the public key of the CA to the CA itself? Well, since we can't introduce another party, for otherwise the loop would never end, the idea is to let the CA, and only the CA, self-sign his own certificate. That is, the certificate of the CA which maps the public key of the CA with the CA's identity is signed with the CA's own private key. These certificates are the so-called self-signed certificates. All the root authorities must self-sign their own certificates.
Indeed, in most browsers and applications there is a list of trusted CA, which are inserted during installation time.
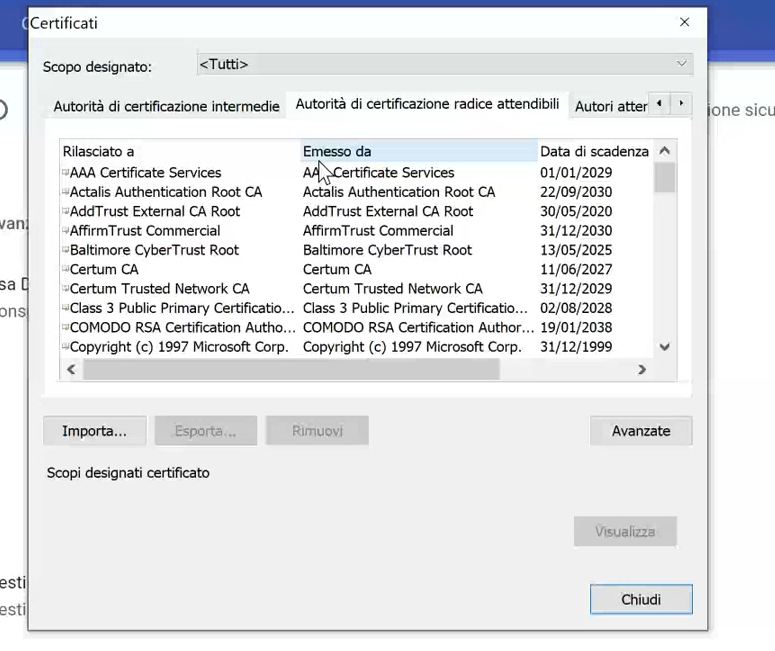
Observation: To check the quality of an SSL site you can use the site https://www.ssllabs.com/.
2.2.1 Cert replay attacks
Notice that even if you see a valid certificate, you still don't know who you are talking to. Anyone could've sent it to you with a *cert replay attack.

The thing to realize however is that, even if such an attack is made, it is not exploitable and leads nowhere. This attack is not meaningful, because the attacker can only reply the valid certificate, and therefore he cannot change the public key contained in it.
3 Proving Knowlege of Secret Key
As we mentioned earlier, we have to ways to prove that we know a private key associated to a public key:
Via digital signature
Via decryption
Its crucial thus to know that validating a certificate is only half the story: the certificate might be valid, but we still need a protocol in place to ensure that who we are talking to actually didnt just steal the certificate but actually owns the private key associated to the public key present in the certificate.
In TLS both of these systems are supported.
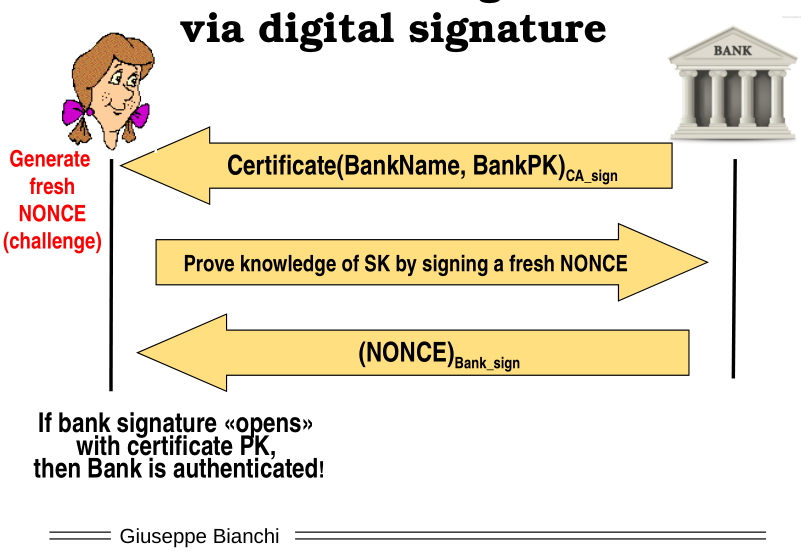
3.1 Via Digital Signature
The bank sends the CA, the client checks if the CA is valid and then sends a nonce to be signed by the bank. The bank, to prove that it has knowledge about the secret key, signs the nonce with the secret key. If the signature is validated using the public key in the CA then it means that the bank has the proper private key.
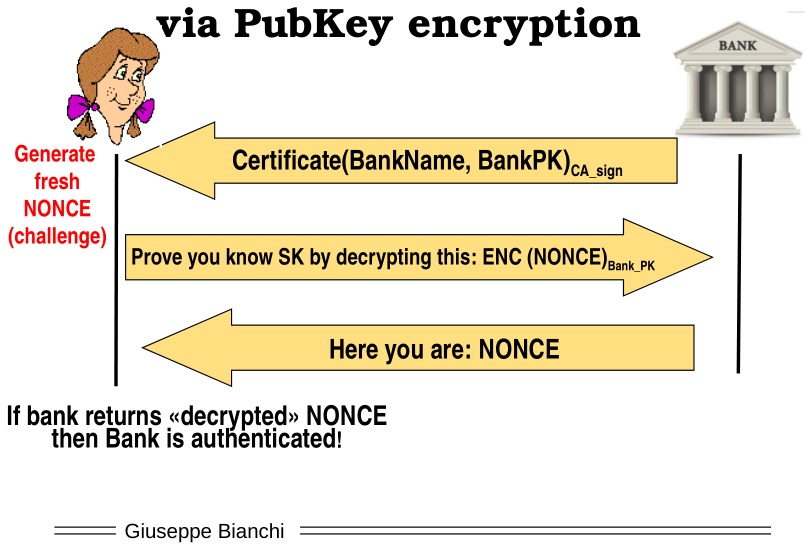
3.2 Via Encryption
This time instead of sending a nonce in clear and asking the bank to sign it, the idea is to encrypt the nonce with the public key of the bank, and asking the bank to decrypt it. If the bank returns the correct nonce, then we know that the bank owns the private key.
3.3 TLS Approach
In TLS when using RSA key transport upon receiving a valid certificate the client does not generate a new nonce, but it uses as a nonce the symmetric key that is later used for encrypting the channel. This key is sent encrypted using the bank's private key.
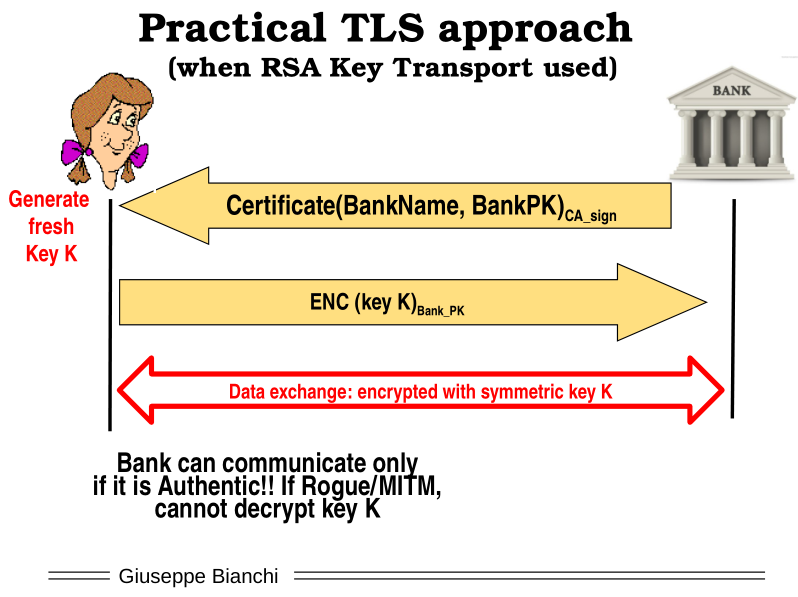
After sometime data will be exchanged encrypted with the symemtric key \(K\). This means that if the bank was not really the bank, the channel is still secure, because only those with knowledge of the private key associated to the public one included in the certificate is able to read the data. In this way server-side authentication is done implicitly.
4 Certificate Chains
The idea is to have a hierarchy of CAs which creates certificate chains: I trust a CA only if that CA is trusted by someone else which I already trust.
