CNS - 29 - Bleichenbacher's Oracle
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides:
Introduction: In this lectuer we will start to understand more in depth the security behind the RSA key transport, and why it was decided to deprecate it.
1 RSA Key Transport
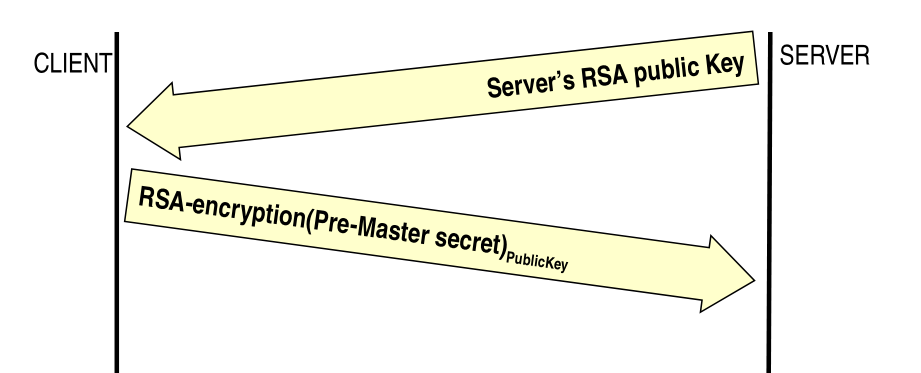
The idea of RSA key transport, which is a possible way to trasnsfer the symmetric key using TLS is taht the server sends the client the server's rsa public key with a certificate signed by a trusted CA. The client then generates a pre-master secret, encrypts it using the server's public key and sends it to the server.
2 RSA is Malleable
The non-malleability property for a cryptosystem may be described as follows:
Given an encryption \(c\) of some message \(m\), the attacker should not be able to create a different ciphertext \(c'\) that decrypts to e message \(m'\) that is somehow related to \(m\).
Notice then that the RSA cryptosystem, if taken as it is, is that is malleable, because, as we saw in the previous section, we had that given the following relationships between ciphertexts
\[C' = r^e C \mod N\]
we have the following relationship between the plaintexts
\[M = M \cdot r^{-1} \mod N\]
3 Chosen Ciphertext Attacks break vanilla RSA
Let us now understand the RSA key transport mechanism is robust against chosen ciphertext attacks.
Consider a ciphertext
\[C = M^e \mod N\]
Our goal is to decrypt it, i.e. to find a value for \(d\) such that
\[M = C^d \mod N\]
To help us in this goal let's assume that we are able to do choosen ciphertext attacks, that is assume we have a decryption oracle which, given a string, it helps us to decrypt that string. To make this problem not trivial the only limit we have is that we cannot submit to the oracle directly the string we want to decrypt.
Notice that with this ability we can immediately find out the secret message \(M\). Indeed, consider the following attack:
We generate a random value \(r\)
Using the random value we construct a new ciphertext
\[X = (r^e \cdot C) \mod N\]
We then ask the oracle to decrypt the message \(X\), and the oracle will return
\[X^d = (r^e C)^d = r^{ed} \cdot C^d = r \cdot C^d \mod N\]
By dividing by the inverse of \(r \mod N\) we get the original message \(M\), which most likely exist (it does not exist only in the case where \(r\) is a multiple of \(q\) and \(p\)).
\[X^d \cdot r^{-1} = r C^d r^{-1} = C^d = M \mod N\]
4 RSA Padding
To make RSA actually usable a standardization (PKCS #1 v1.5) introduced the idea of RSA padding, which solves a bit of problems, such as:
If the message is \(m=1\), then by default \(C = m^e = 1^e = 1 \mod N\).
The basic RSA is vulnerable to a Choosen Plaintext Attack (CPA), and thus IND-CPA property is broken and we don't have, by default, semantic security.
When using RSA then the plaintext message is not encrypted as it is, but before it gets modified as follows

The content of the padding is:
The first two bytes are always added there as fixed values.
Then we have eight random bytes, which acts as a sort of initialization vector, which protects against CPA. These bytes are random but different from \(0\).
Then we have a byte equal to \(0\)
Finally, we have the application data, which is no more than \(k-11\) bytes, where \(k\) is the size of the RSA modulus in bytes.
For example, with RSA-1024, we can encrypt up to 117 bytes per packet.
4.1 (Actual) RSA Key Transport
Let us now revisit the process of transfering the key using RSA with the new information we have described so far.
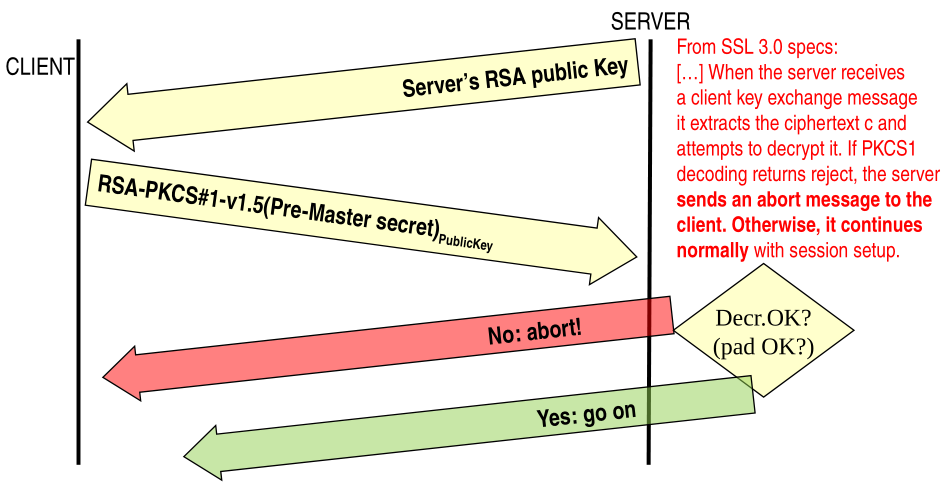
Notice in particular that in the SSL v3.0 protocol it was specified that if decryption fails at the server side, then the server has to return an error message to the client. But if the decryption does not fail, then also the padding did not fail. Thus we have a way of understanding whether the padding is correct or not. That is, we have a padding oracle.
5 Bleichenbacher's Oracle
Daniel Bleichenbacher developed in 1998 an adaptive choosen plaintext attack against RSA PKCS #1 which works if you have at least \(2^{20} \approx 1 \text{million}\) messages, which is actually a very feasible number of messages.
The vulnerability was then corrected in TLS v1.0, but, as we have already seen with the original padding oracle attack, fixing such an attack is always hard, and this vulnerability got explointed until \(2019\). Finally TLS v1.3 decided to remote RSA key transport and use only the Diffie-Hellman Key Exchange.
The bleichenbacher's oracle works as follows:
Our goal is to decrypt the ciphertext
\[C = M^e \mod N\]
To do this we pick a value \(r\) and construct a new ciphertext
\[C' = C \cdot r^e \mod N = (M r)^e \mod N\]
Notice that by multiplying the ciphertext by \(r^e\) I'm essentially multiplying \(r\) with the plaintext.
We then send this new ciphertex to the SSL v3.0 server, which in this attacks acts as our oracle. The server specifically will tell us if the plaintext \((M r)\) starts with \(0002\) or not. This knowledge leaks information about \(M\), which can be used to completely decrypt it with a sufficiently large number of attempts.
The specifics of the attacks are pretty technical, we can understand the idea behind the bleichenbacher's oracle with the following toy example.
5.1 Toy Example
Instead of having a padding which tells us whether if the message starts with \(0002\) or not, we'll assume to be working with a single bit as padding, which means that our server will tell us if the message starts with a \(0\) or starts with a \(1\), thus reavealing a single bit of our message.
Consider then a message of length \(\log_2 n\) bits, where \(n\) is the value for the modulus. With this we'll be able to decrypt the entire message with \(\log_2 n\) attempts. Finally, consider the following RSA parameters:
\(p = 13, q = 19, n = 247\) (8 bit)
\(e = 29\), which means \(d = 149\)
Assume then you see the encrypted message \(C = 90\), and we want to retrieve the original message \(M\). We know that \(M = 90^{d} \mod N\), but of course we don't know \(d\). The attacker then sends to the server the following ciphertexts:
\(C \cdot (2^1)^e \mod N\)
\(C \cdot (2^2)^e \mod N\)
\(C \cdot (2^3)^e \mod N\)
\(C \cdot (2^4)^e \mod N\)
\(C \cdot (2^5)^e \mod N\)
\(C \cdot (2^6)^e \mod N\)
\(C \cdot (2^7)^e \mod N\)
\(C \cdot (2^8)^e \mod N\)
Eachtime we are testing if the plaintext of the form \(2^i \cdot M\) starts with \(0\) or \(1\). For example in the first attempt we test if the plaintext \(2M\) starts with \(0\) or \(1\), while in the fourth attempt we test if the plaintext \(16M\) starts with \(0\) or \(1\).
Suppose then the server returns the following sequence of bits
\[0, \,\,\, 1, \,\,\, 1, \,\,\, 1, \,\,\, 0, \,\,\, 1, \,\,\, 1, \,\,\,\ 1\]
By understanding whether the plaintexts of the form \(2^i M\) start with \(0\) or \(1\) we can reduce the possible range in which to find \(M\). In particular we get:
If \(2M\) starts with \(0\), then \(M \in (0, 63)\) or \(M \in (124, 187\).
If \(4M\) starts with \(1\) then \(M \in (32, 61)\) or \(M \in (156, 185)\).
If \(8M\) starts with \(1\) then \(M \in (47, 61)\) or \(M \in (171, 185)\)
After the eigth bit we are able to break the last tie and obtain the specific value of \(M\).
Observation: From all of this we can infer that as long as one bit of information is known, then all the ciphertext is known as well, and thus RSA is as secure as a single bit.
5.2 Parity Attack
As a corollay we can perform the same attack if we have a service, like a shop, with rejects RSA-PKCS#1 encrypted requests for an odd number of items. That is, if we send an even number of items we get a 1 (OK), and if we send an odd number we get a 0 (NOT OK).
As long as we can gain information about the parity bit of any plaintext message, that is as long as we have a parity side channel (parity oracle), we can break RSA by essentialy implementing once again Bleichenbacher's Oracle.
5.3 Is it pratical?
Notice that, unlike the padding oracle, which had to be done on the specific TLS session and was thus very hard to actually transform into a pratical attack, the Bleichenbacher's Oracle is much more pratical, because I can obtain the encrypted message that a client sends to a TLS server on day \(0\), and then up until the day that the server changes his public key I can try and decrypt such a message, which contains the pre-shared secret. Once I get that I'm also able to break all the subsequent TLS messages.
5.4 In the wild
The Bleichenbacher's Oracle was discovered in 1998 and affected SSL up to SSL v3.0. It was corrected in TLS v1.0 but then a series of side channels opened up the Bleichenbacher's saga:
Klima et al. (CHES 2003)
Cross-Tenant Side-Channel Attacks in PaaS Clouds (CCS 2014)
Attack to QUIC (CCS 2015)
DROWN (USENIX 2016)
Return of Bleichenbacher's Oracle Threat (USENIX 2018)
The 9 lives of Bleichenbacher's CAT - cache attacks (IEEE S&P 2019)
5.4.1 DROWN attack (2016)
In 2016 they discovered that a lot of servers were still permetting a downgrade to SSL v2.0. These server were thus easy to expose since the oracle is available on those server.
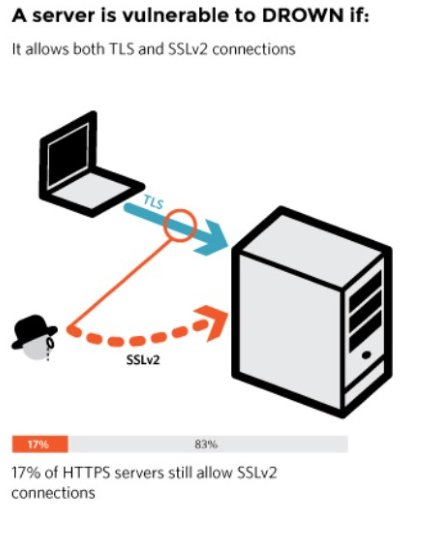
They then found that even those server which has an upgraded version of SSL/TLS, were vulnerable becauase they shared their public key with a vulnerable server that supported only SSL v2.0.
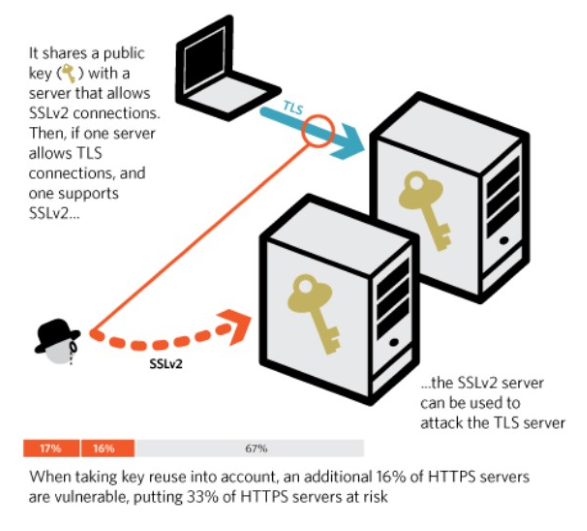
Overall 1/3 of the server were found vulnerable to this type of attack.
5.4.2 ROBOT Attack (2018)
A guy named Hanno Bock started to test Facebook, and discovered by that in Facebook he could reproduce a padding oracle by sending wrong messages and exploring less tested path of the codebase. He then contacted Facebook, and Facebook fixed the particular issue. But then he tried again and he found another vulnerability. At this point he called other guys for a big, systematic analysis and many vulnerabilities were found in many different devices.
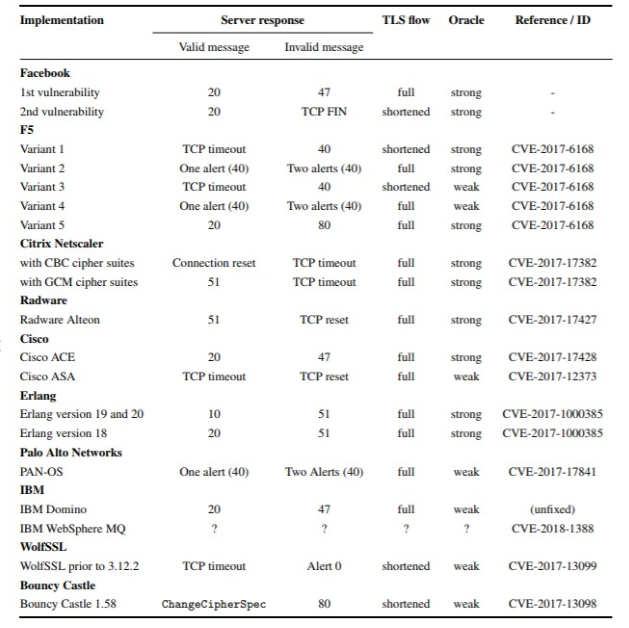
Listen to the talk explaining the attack:
5.5 Countermeasures
Other than changing the way padding is implemented in the RSA key transport to a new standard called PKCS#1-v1.5 (RSA-OAEP), which it was denied because it was a way too big change, the only possible solution is to forget RSA key transport, which is the path taken by TLS v1.3.
6 Take-Home Messages
The main messages to take from are:
Once you make a major error during standardization, like it was done for the RSA key transport in TLS (they standardized an oracle without knowing it was an oracle), you cannot just change the standard, you also have to change the implementation and to make the implementation rock solid, which rarely happens.
The story of the Bleichenbacher's Oracle is very much akin to the story of the MAC-then-encrypt saga. The point is that both of these vulnerability opened up the possibility for a Choosen Ciphertext Attack (CAP). Fixing these types of attack is truly hard, and the best to do is actually to remove the vulnerable part of the protocol altogether.
Even people who are used to pratical security might not fully grasp cryptography attacks.