CNS - 30 - The Failure of PKI
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: (26-cert-trans.pdf)
Introduction: In this lecture we have discussed the fact that the security assumption behind PKI can actually be quite problematic, and we have seen a solution to the problems of "fake certificates" by introducing an old data structures called merkle trees.
1 Fakes Certificates
An important pillar in web security is the fact that CAs are trusted entity.
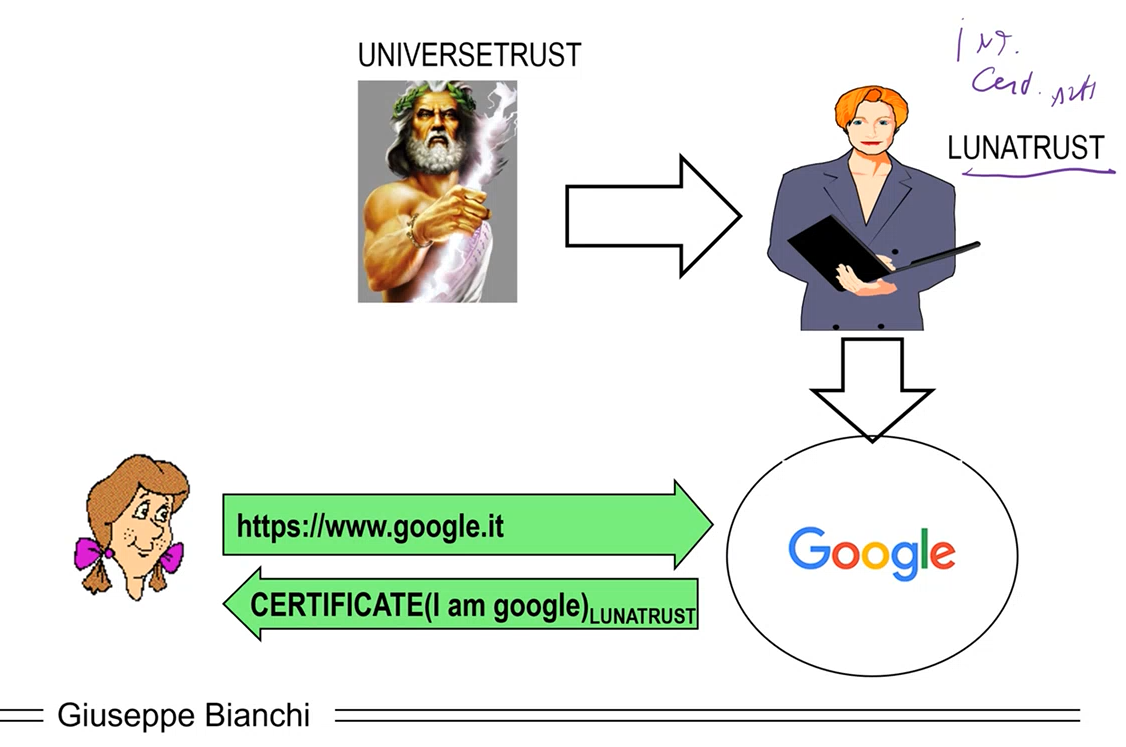
When we are given the certificate our browser then does the following checks:
Checks if the certificate is valid
Checks if the entity present in the certificated owns the corresponding private key.
The assumption that requires CA to be trusted entities is becoming always harder to maintain, because, especially in the post-Snowden world, information came out that governments themselves were attacking the PKI infrastructure to do mass surveillance. This is the problem of fake certificates.
Observation: Some further information regarding the topic:
TLS Proxies: Friend or Foe?
Google's VALID fake certificates mistakenly issue (TurkTrust, 2012)
When we used the word "fake certificate" we do not mean a certificate that has been forged by an attacker, nor do we mean technical attacks that target the generation/checking process of the certificate (such as the 2020 curvball attack).
What we mean with the phrase "fake certificate" we mean certificates signed by a certain trusted CA, which is controlled by someone else. The problem in this case is that the certificate itself is valid, and the browser validates it.
Assume for example that the leader of the country forces the local authority working on that country to generate a certificate with a specific public key (the leader owns the associated private key). Notice that in this case with the only checks that we've mentioned before the final user cannot tell if the certificate is legit or not.
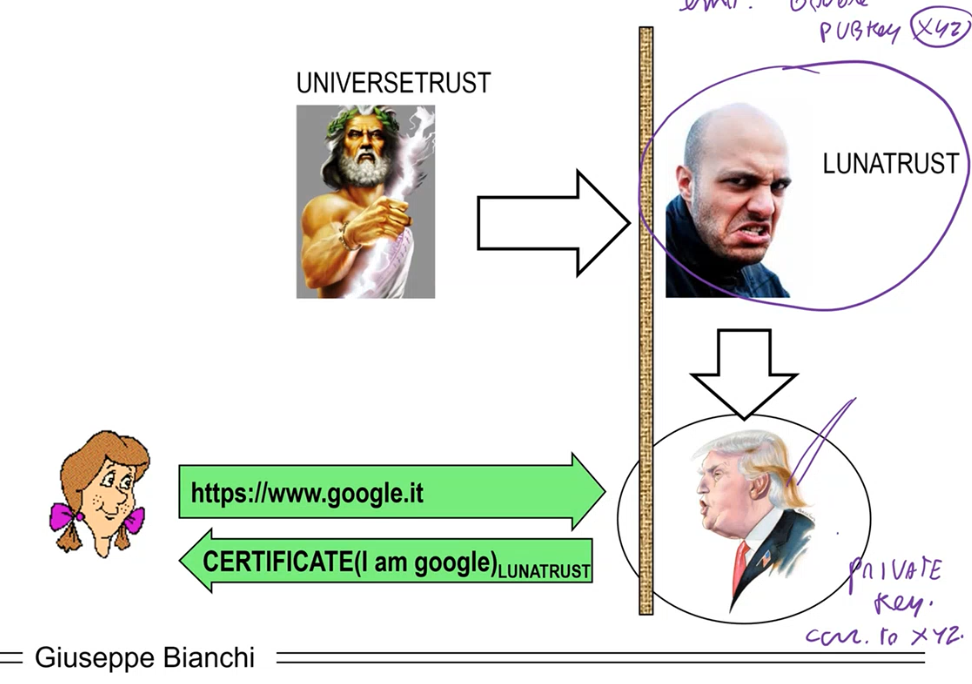
If a few years ago this type of attack would not have been realistic, today we have evidence that it is a real threat to the security of the Public Key Infrastructure (PKI-Model). This means that the security of the PKI model is broken by the power of government threaths.
2 How to Secure a File
The problem we want to solve is how to secure a file when there is no large secure storage available.
Using techniques we already know we could approach these problem in two steps:
First we compute a "fingerprint" of the file via a cryptographic hash function. Even if the file is large, the final fingerprint is very small.
Then we can secure the fingerprint by either copying it in a secure storage or by digitally signing the hash fingerprint with our private key.
The problem with this approach is that its not very scalable. Consider for example a p2p network in which a very long message is transmitted along with its signature.

Typically the network divides the message into independent chunks, which are sent by the various peers. To actually verify the integrity of the message the client has to download all the chunks, the signature, and only then it can check the integrity check can be performed. This is clearly vulnerable to situations where bad chunks are injected by malicious users, not to mention that the solution showcased before does not cover the case where only partial integrity is required. We thus need a better approach.
Notice that computing a signature for each chunk of the message is, once again, not a scalable solution, because of these two factors:
Computational overhead: for each chunk we need to compute a signature, which has a higher cost than a simple hash computation.
Storage overhead: the size for a single signature can vary between 64 and 256 bytes using modern public crypto systems, which means that for chunks of 500 bytes adding such signature would mean a 50% overhead in storage size.
Strip-type attacks: if we don't take extra care we lose the ability to check the integrity of the whole file (such as adding sequence numbers in each chunk) we also become vulnerable to a strip-type sort of an attack, which is similar to the trunction attacks we talked in a previous lecture, in which the attacker simply removes some packets and the final client does not know whether it has received all the message or not.
3 Merkle Tree
The theory of merkle trees was developed in 1978 and is now becoming more popular again thanks to the Bitcoin network.
The basic idea behind merkle trees is that, suppose I have a large file. Then I can divide it in half, and compute for each half a fingerprint. At the end I thus have two fingerprints: \(H_1\) and \(H_2\). I can then take these two fingerprints, concatenate them together, and hash the resulting string to obtain a third fingerprint \(H_3\). Intuitively this computation is equivalent, in terms of security, to the fingerprint obtained by hashing the entire file.
This idea can be extended as is shown in the following image
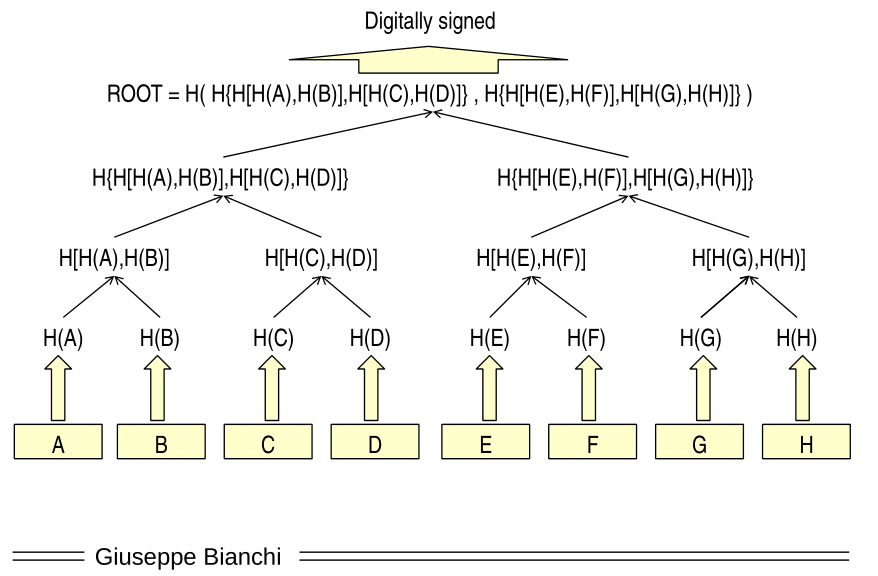
Notice that since hash are much cheaper to do compared to digital signing something, the extra computation added in the merkle tree is really not that much.
With this structure we can then check the integrity of each piece of the file by using the so-called "siblings" in the tree, which are typically one per-level of the tree, and thus are at most \(O(\log N)\).
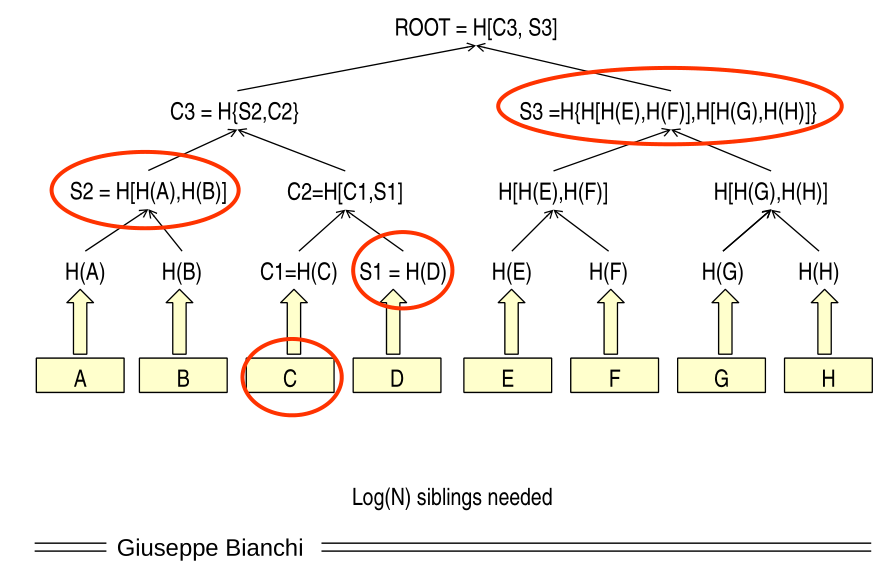
Notice that the anchor trust of a merkle tree is the root, which has to be secured through a digital signature. Thus, when we check the validity of a node, other than the node itself and its siblings in the merkle tree, we still need to know that the root was properly signed.
Comparing this solution to the previous one, we can see that in this case the fingerprint of the entire file is no longer a single hash computation, but is rather the entire merkle tree. The increase in complexity in this new solution, which is actually not that much, offers a new advantage: the ability to check the integrity of chunks of the file.
Consider then the following application: when a new certificate is generated you can simply transmit the various siblings needed to reach the root, which is the only thing that is actually stored in the global DB of certificates.
Notice that both the data (the certificate itself), and its siblings in the merkle tree can be sent in clear and can be modified by the attackers. This does not break the system because, for as long as the hash used has the anticollision property, and as long as the root is digitally signed and cannot be modified, then the modified versions of the data/siblings will give a different root, and thus the check will fail.
3.1 Possible Applications
There are various possible applications which benefit from the flexibility offered by merkle trees, such as:
Efficient storage in blockchains
Google's Certificate transparency
File Chunk validation
One-time signatures
Node authentication
Signature spreading
3.1.1 Node Authentication
Assume you have \(1\) million devices and you want to ensure that the code you put in all those devices is not modified. What you can do then is to simply put in the code of each node \(20\) siblings, and then you expose in a public site the signed root of the tree. With this approach each device can construct the merkle tree and verify if the root is valid.
3.1.2 Extend with Time
The idea is to define a time-slot (Bitcoin uses a \(10\) min timeslot, while Google a \(1\) day timesllot) in which all the data to fingerprint is collected. Then, at the end of the timeslot, we construct a markle tree with the data and we secure the root, either by signing it or by hiding it
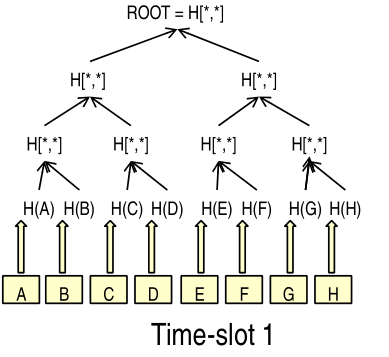
The next "day" we continue on the second timeslot with the same idea collecting new data
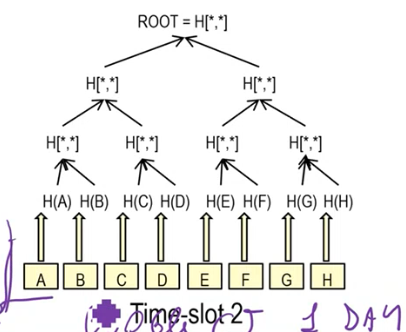
At the end of the day then we take the previous root (the root of the merkle tree computed in the first timeslot), and we combine it with the current root, to obtain a new root.
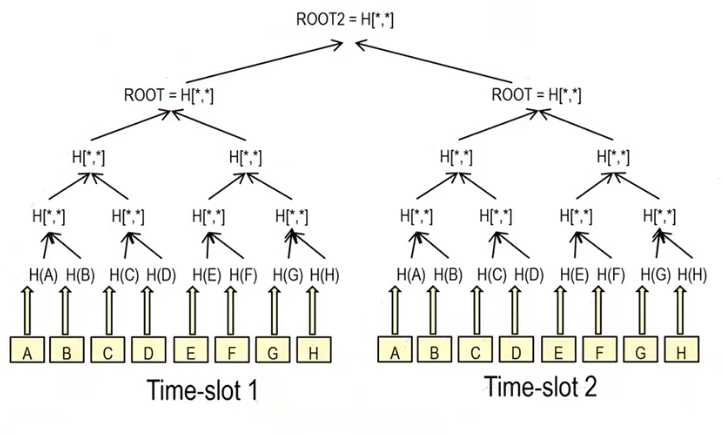
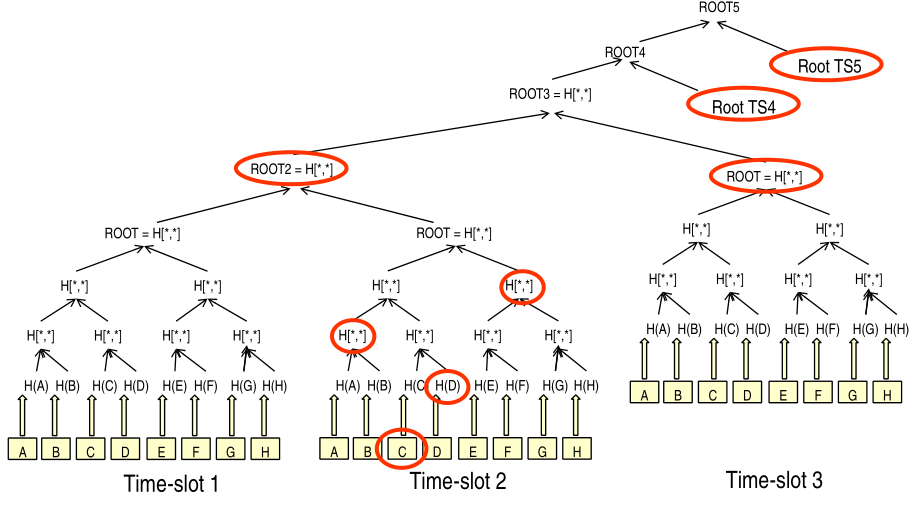
To validate a given node then we need the siblings for the tree to which the node belongs to, the root of the previous timeslot and the roots of the next timeslots.
3.1.3 Blockchain Usage
In the blockchain technology merkle trees are used to validate the integrity of all the transactions that are inserted in a single block of the blockchain.
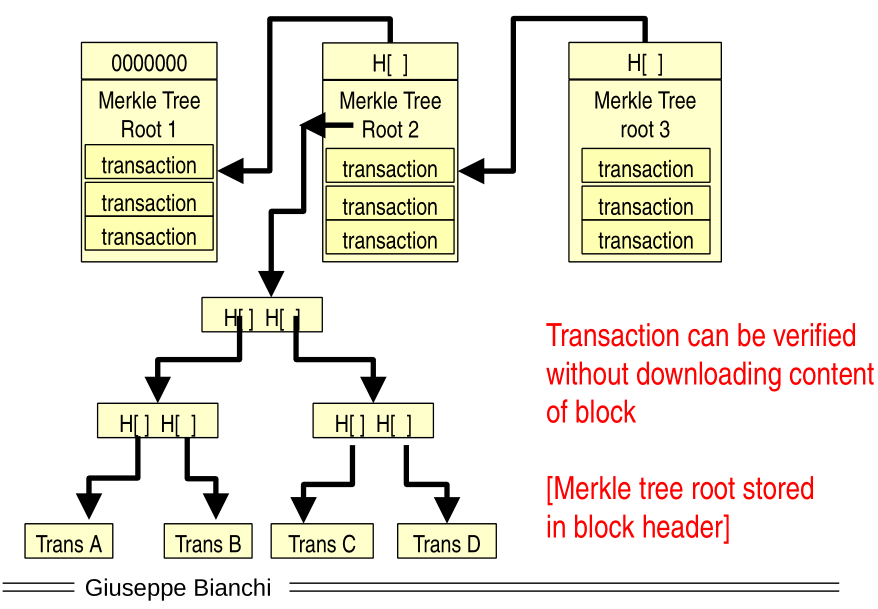
The merkle tree root included in the block header act as a single cryptographic summary of all the transactions present in the block. Each block then contains the hash of the previous block as to create an unbreakable crypto chain.
4 Certificate Transparency
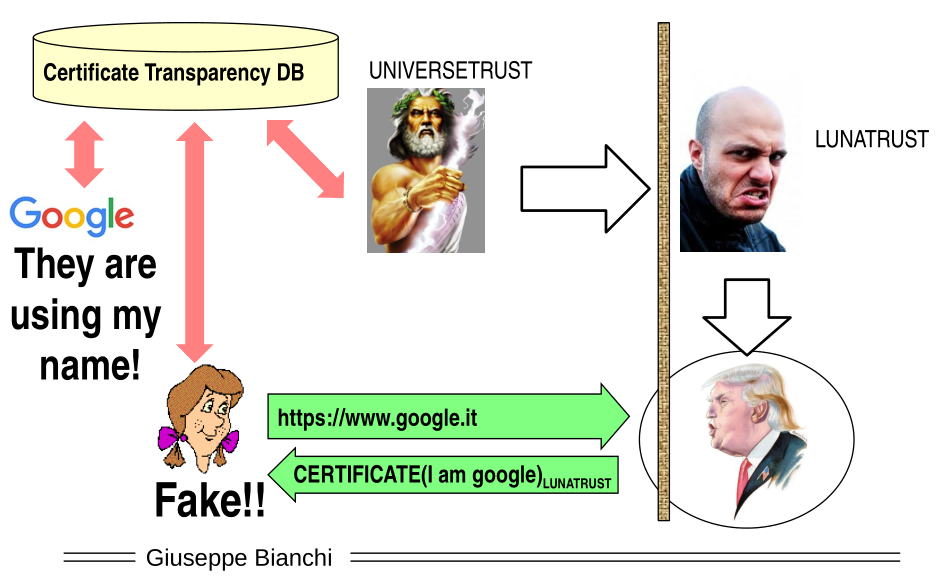
To solve the problem of "fake certificate" Google had the idea of using a worldwide DB called a Certificate Transparency DB, which contains all the certificates in the world and which anyone can check.
With this approach the attack we showed previously can be mitigated as follows:
If LUNATRUST (the intermediate CA) does not insert the "fake certificate" in the global DB, then the user, after having check the integrity of the certificate, can check its present in the global DB. In this case this third check fails, and so the user rejects the certificate.
If LUNATRUST (the intermediate CA) does insert the "fake certificate" in the global DB, then, for example, Google can periodically check and see if anyone else has added a "fake certificate" using their name.
Graphically,
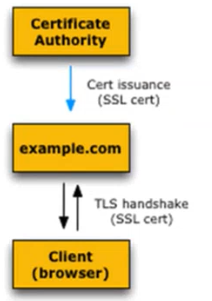
To implement such a solution merkle trees are used. Consider in particular the way certificate were generated previously
Now this scheme changes as shown below
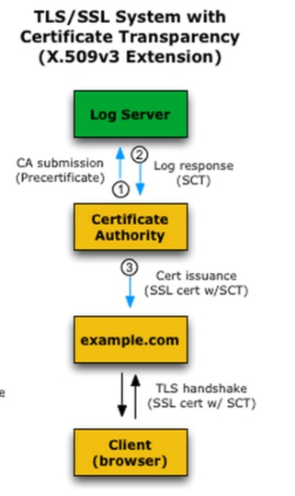
The idea is that when a CA receives a request to generate a new certificate, it submits the certificate into the log server (which manages the global DB). The log server then offline inserts the certificate inside a merkle tree and in response it gives back the CA the list of siblings necessary to reach the root for that particular certificate, as well as the timestamp needed to understand in which timeslot the certificate is located. This informations are then sent to each client that wants to connect in order to verify the certificate.
With this new approach when the client has to verify the validity of a certificate it does three checks:
It checks if the certificate is valid.
It checks if the owner of the entity being certified has the corresponding private key.
It checks if the certificate is present in the global db by querying the log server with the certificate and the list of siblings received by the server.
For more details about this initiative you can look up the site certificate transparency. This type of "extra checking" is also called extended validation (EV).
Observation: Notice that the certificate transparency DB is not complete a blockchain, because it only enforces transparency and it allows companies like Google to revoke certain certificates. It does not guaranteee you that only "true" certs are stored. A blockchain must also guarantee that only "true" data is in the DB, which is not something that you solve with a Markle Tree.