CNS - 35 - Secret Sharing II

Lecture Info

Date: [2020-12-10 gio 11:30]
Lecturer: Giuseppe Bianchi
Slides: (40-ss.pdf)
Introduction: In this lecture we continued our discussion of secret sharing techniques.

1 The Real Shamir Scheme

Notice that in the (t, n) scheme presented in the last lecture we don't have perfect secrecy, because if we collect a number $m < t$ of shares then the probability of guessing the secret is much lower thatn it would be if we didnt have any shares. To get perfect security the actual Shamir scheme actually runs in modular arithmetic, with a prime modulus $p$.

Doing modular arithmetic with a prime number is pretty annoying for modern processors, since they can only work with modular 32bit/64bit arithmetic. Thus you need to create a software layer for taking care of this, which slows down the entire process. Also, even though we require to work in modular arithmetic, the modulus $p$ does not have to be large. This is because the security of this scheme does not depend on a problem that is hard in terms of computational complexity, but rather it offers perfect secrecy, that is its based on a theoretical result.

1.1 Example with $p=101$

Suppose then our secret has to be in the range $s \in (0, 100)$ and we want to have a (3,4) scheme. Then we can use the prime $p = 101$ and consider the following polynomial in the field $\mathbb{F}_p$

\[p(x) := 3x^2 + 52x + 32 \mod 101\]

Let us now compute the shares for each participant

$\text{share}_1 = (1, p(1)) = (1, 87)$
$\text{share}_2 = (2, p(2)) = (2, 47)$
$\text{share}_3 = (3, p(3)) = (3, 13)$
$\text{share}_4 = (6, p(6)) = (6, 48)$

We can then compute the lagrange coefficient for each share

\[\begin{split} \Lambda_1(0) &= (0 - x_2) \cdot (0 - x_4) \cdot \Big[ (x_1 - x_2) \cdot (x_1 - x_4)\Big]^{-1} \mod 101 = 63\\ \\ \Lambda_2(0) &= (0 - x_1) \cdot (0 - x_4) \cdot \Big[ (x_2 - x_1) \cdot (x_2 - x_4)\Big]^{-1} \mod 101 = 49 \\ \\ \Lambda_4(0) &= (0 - x_1) \cdot (0 - x_2) \cdot \Big[ (x_4 - x_1) \cdot (x_4 - x_1)\Big]^{-1} \mod 101 = 91 \\ \end{split}\]

To reconstruct the secret we can do the following

\[\begin{split} S &= y_1 \cdot \Lambda_1(0) + y_2 \cdot \Lambda_2(0) + y_4 \cdot \Lambda_4(0) \mod 101\\ &= 87 \cdot 63 + 47 \cdot 49 + 48 \cdot 91 \mod 101 \\ &= 32 \\ \end{split}\]

Assume now that I only know the third and fourth share, while the share of the first guy can be an arbitrary value

\[\begin{split} S &= d \cdot \Lambda_1(0) + y_2 \cdot \Lambda_2(0) + y_4 \cdot \Lambda_4(0) \mod 101\\ &= d \cdot 63 + 47 \cdot 49 + 48 \cdot 91 \mod 101 \\ \end{split}\]

When you look at these numbers by varying $d$ between $0$ and $100$ you will see that these numbers will never repeat and that they will cover all the possible values, meaning that for every possible share you get every possible share and vice-versa. This examples lets us understand intuitively why if $p$ is a prime number then $S$ is uniformly distributed in $\mathbb{F}_p$.

1.2 Ideality

We have now discussed, at least intuitively, that the shamir scheme offers perfect security. Let us now tackle a second point: is it also efficient? To this end we introduce the criterion of ideality.

Consider then the following question: in a perfectly secure scheme can a share be smaller than the secret? It comes out that for informational theoretic reasons that the share cannot be smalelr than the secret. Intuitively this result can be argued as follows: in a $(t, n)$ scheme, the last share must bring exactly as much information as the secret itself, while the first $t-1$ shares bring no information.

While the size of the share cannot be lower than the secret, it can however be larger. A scheme is then said to be ideal if the size of the share is equal to the size of the secret.

\[|\text{share}| = |\text{secret}|\]

This is why the Shamir scheme is ideal, while other schemes, such as the Blakely scheme, are not ideal.

2 Secret Sharing for SMC

The idea behind Secure Multi-Party Computation (SMC) is doing computation on data without seeing input but with the possibility to compute specific outputs.

2.1 Layman example of SMC

Consider a situation in which the people count indipendently the number of accesses to their websites and the internet provider wants to count the total number of accesses in order to compute certain statistics.

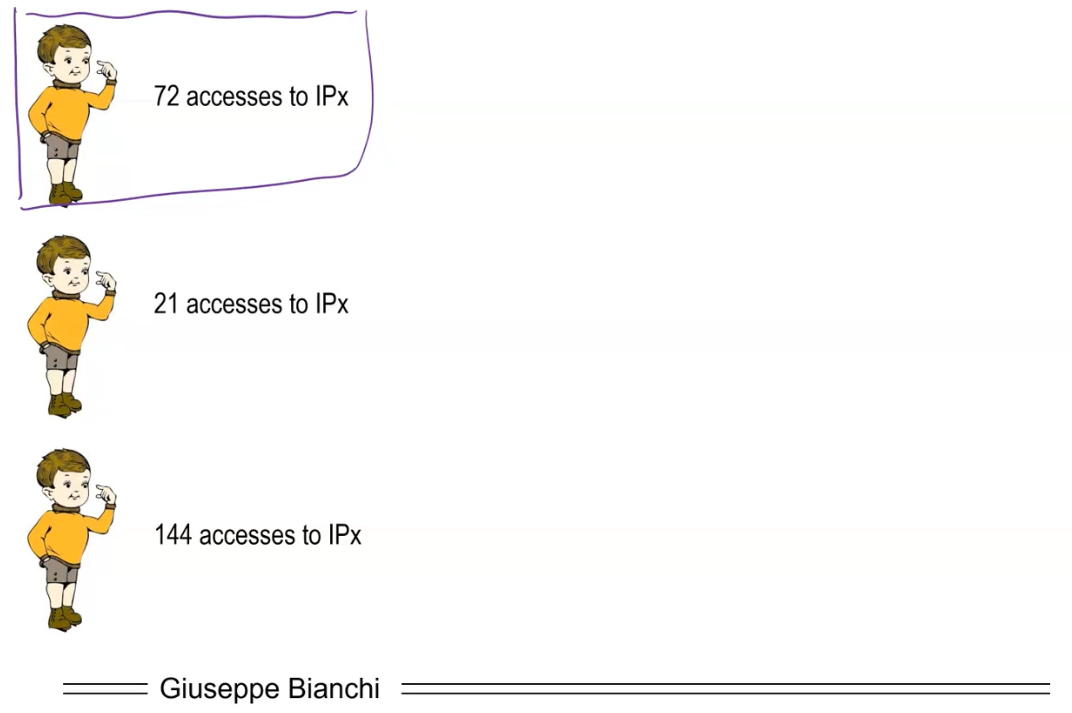
The basic idea would be to just send each value to the central authrity and let it compute the total sum. This means however that the centrial authority is able to see the accesses to each site, something which the users could potentially want to hide for privacy reasons. Is there a method which lets us obtain the sum without actually revealing the single accesses?

The idea is to have two sepearate and independent authorities, authority A and authority B, collect from each party 2 numbers, which represent the shares of a (2, 2) secret sharing scheme.

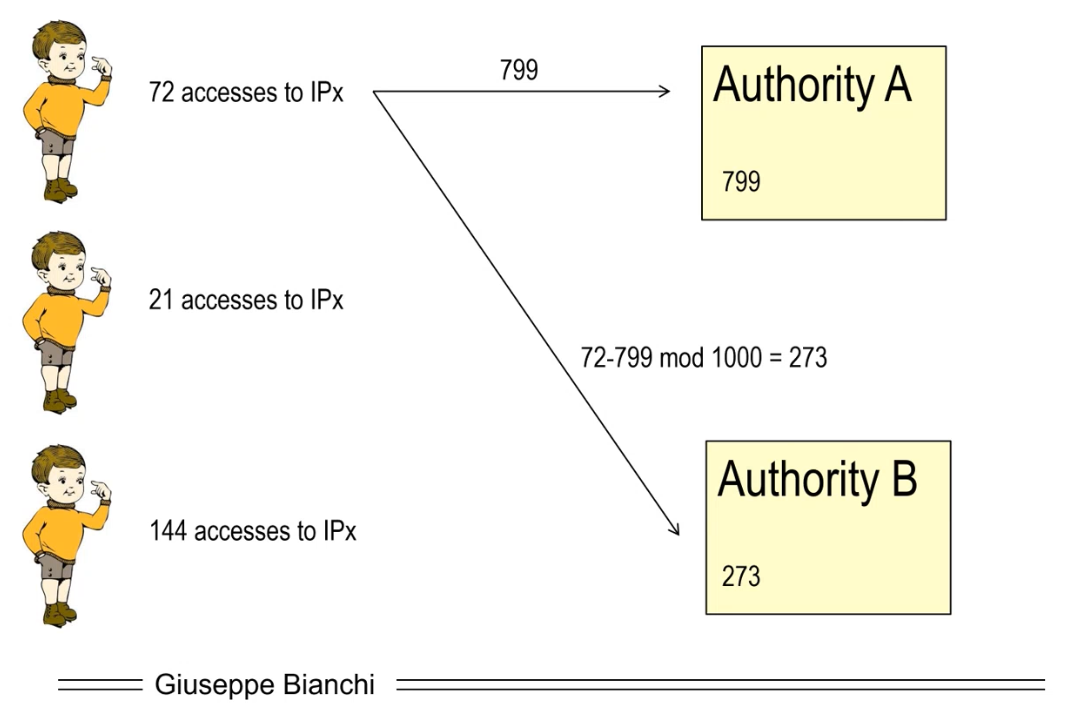
Once each authority has all three numbers, they sum them and produce in output a single number. Once these numbers are summed, we get the original sum back, even though the single numbers were never disclosed to the authorities.

This method works because of a linear property that tells us that the sum of the shares is equal to the share of the sum.

2.2 Homomorphic property

For a shamir scheme (as well as the trivial scheme) there is a beautiful property which is called the homomorphic property which states that the sum of the shares is the share of the sum.

More in detail, consider two secrets, $S_F$ and $S_G$, and consider two polynomials $f(x)$ and $g(x)$. The polynomial $f(x)$ was constructed to create the shares for dividing the secret $S_F$, and this also applies to $g(x)$ with respect to $S_G$.

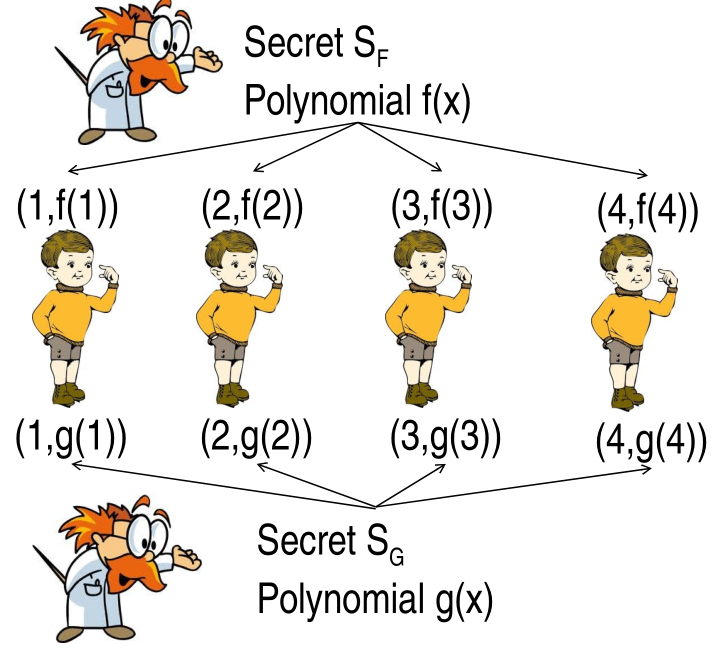
Given two shares $f(i)$ and $g(i)$ by the homomorphic property we get

\[f(i) + g(i) = (f + g)(i)\]

Thus, revealing $t$ composite shares reveals the sum of secrets but does not reveal the individual secrets.

2.3 History of SMC?

More precisely SMC are techniques that allow the computation of the result of a function without revealing the input data. SMCs allow for several use-case scenarios:

Business/financial.
Security.
Medical.
Traffic monitoring.

Notice however that even though SMC have many real-world applications, it is still largely underrated and typically avoided because, for historical reasons (that go back to 1982), the first techniques for doing SMC were really heavy.

Historically SMC was born was as a 2-party computation (Yao's millionare problem, 1982), where Yao considered the following problem: suppose you have two persons and you have to discover which one of them is richer without asking them directly for how much money they have.

After 2010 many faster and easier techniques came out, and a guy opened up a company named unboundtech which tries to find solution to problems where you need to operate on data using untrusted hardware.

2.4 What is SMC?

Let us now formalize better the problem.

We have $N$ parties $P_1, P_2, \ldots, P_n$, each one with a value $z_i$. Our goal is to compute a function $f(z_1, z_2, \ldots, z_n)$ such that

The result is public.
No information is given on input values $z_i$.

This problem can be solved in general, but the solution for the general case is heavy and complex. In particular cases however if the function $f(\cdot)$ has a particular form, then there exists very efficient solutions for SMC using secret sharing schemes. This is the case, for example, when $f(\cdot)$ is just weighted sum such as

\[f(z_1, z_2, \ldots, z_n) = \alpha_1 z_1 + \alpha_2 z_2 + \ldots + \alpha_n z_n\]

2.5 SMC for Weighted Sums

When $f(\cdot)$ is a weighted sum and we can use a trusted third party then we have the following

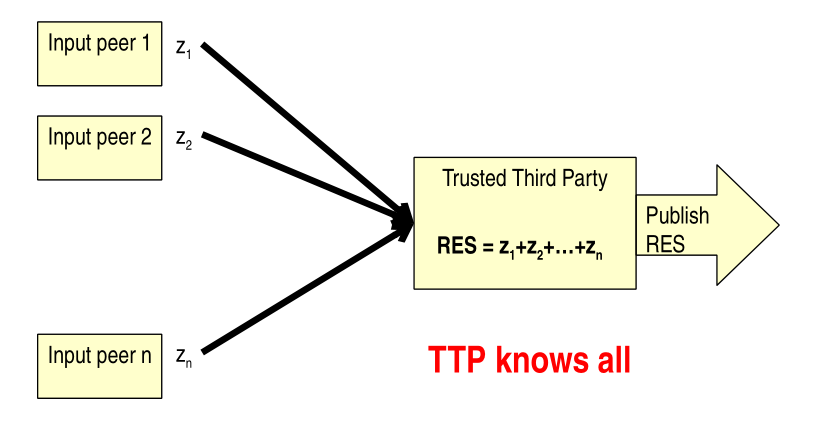
If instead we don't have a trusted third party we can simulate it by distributing our shares over multiple untrusted third parties, each of which is assumed to follow the honest but curious model, which means that they do not cheat, but they also do not guarantee the confidentiality of the data they see.

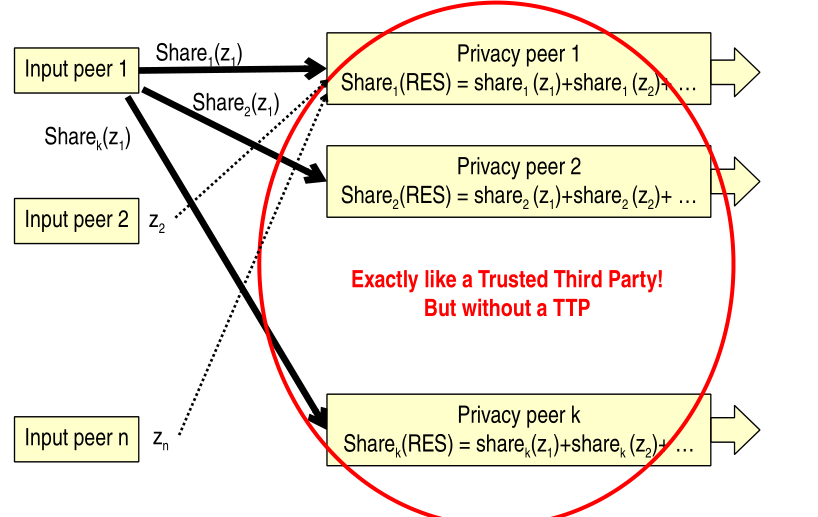
Notice that an arbitrary secret sharing scheme may be used. The only requirements is that it has to have the homomorphic property.

2.5.1 Deployment Issues

The input peers have to be at least $3$, because if they are $2$ one aprty may know other party data by subtracting from the final result. Thus $n$ is usually large, and it can be very large, because the scalability does not depend on such number.

The aggregators instead are the privacy peers, which must be at least $2$, but the more the better for security and robustness.

Finally note that the privacy peers can be the individual peers themselves.

2.5.2 Construction

Each input peer $i$ does the following:

Input data $z_i$
Generates a polynomial $p_i(x)$ of degree $t-1$ with $z_i$ as a known term.
Privately sends shares $p_i(1), \ldots, p_i(k)$ to privacy peer $1, \ldots k$.

Each privacy peer $m$ does the following:

Collect input shares $p_1(m), p_2(m), \ldots, p_n(m)$.
Compute $\text{RES}(m) = p_1(m) + p_2(m) + \ldots + p_n(m)$.
Publish aggregated result $RES(m)$

The public can then reconstruct $\text{RES}$ from sufficient number of $\text{RES}(m)$.

2.5.3 $(k, k)$ schemes are better

Notice that $(t, n)$ schemes are complex, and we would like to make the scheme as simple as possible. The idea then is to roll back and use a $(k, k)$ trivial secret sharing where the measurement is $z$ and we have $k$ shares:

$\text{share}_1 = r_1$
$\text{share}_2 = r_2$
...
$\text{share}_k = z - r_1 - r_2 - \ldots$

With this approach we also dont have to worry about implementing modular arithemtic on a prime field. We can simply use ordinary modular arithmetics.

2.5.4 No privacy peers

Suppose that I have three input peers and three privacy peers. Typically you would have a bipartite graph where every input peer contacts every privacy peer.

Notice however that we can also create a system in which we have no privacy peers. This requires however that every input peer also acts as a privacy peer. To make it clear why we meant let's consider the following example: a group of friends wants to buy a birthday present to one of their friends. To do so they come together with some amount of money. Each of them however does not want to reveal how much he/she has contributed to the total. Assume also that the maximum money is 100$ (we work mod 100).

Each peer generates two random numbers $R_1$ and $R_2$, and sends to one peer the second one $R_2$ and to the other peer the value obtained by subtracting the sum of the two random values to the money put in by the peer.