CNS - 36 - Verifiable Secret Sharing
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: (41-vss.pdf)
Introduction: In this lecture we introduce more robust technies of secret sharing, verifiable secret sharing, that also works when the parties are not honest.
1 Verifiable Secret Sharing
A secret sharing scheme is called verifiable secret sharing if it works also under the assumption that the privacy peers are not only curious, but also not honest. That is, it covers the case where the privacy peers can also lie.
2 Feldman Scheme
The first VSS (non interactive) scheme was proposed in 1987 and its called the Feldman VSS scheme. This scheme is frequently used as the basis for distributed schemes.
The scheme is an extension of an ordinary \((t, n)\) shamir scheme.
2.1 Dealer
The dealer generates a random polynomial \(p(x)\) with degree \(t-1\) and with \(P(0) = s\)
\[p(x) = s + a_1x + a_2x^2 + \ldots + a_{t-2}x^{t-2} + a_{t-1}x^{t-1}\]
where \(a_i\) are random terms in the suitable modular range. Once having done that, we distribute one share to each of the \(n\) parties
\[(x_i, y_i) = y_i = p(x_i)\]
The additional step done by the dealer Feldman scheme is the following one: for each coefficient of the polynomial as well as for the secret the following values are computed and broadcasted in public
\[\begin{split} c_0 &= g^{s} \mod p \\ c_1 &= g^{a_1} \mod p\\ &\,\,\, \vdots \\ c_{t-1} &= g^{a_{t-1}} \mod p \end{split}\]
Notice that, at least in principle, the broadcasting of these values does not reveal anything about the coefficient values, because as long as the value of the prime \(p\) is sufficiently large, than the DLOG problem is computationally unfeasible. These values are called commitments, because they allow you to understand whether or not the coefficient of the polynomial were actually used.
2.2 Verifier
Consider now then the party \(i\) receives the share \((x_i, y_i)\).
When \(i\) reveals his share, the other parties can check if the value revealed by the party \(i\) is correct by computing the following value (working \(\mod p\))
\[\begin{split} & \;\;\; c_0 \cdot c_1^{x_i} \cdot c_2^{x_i^2} \cdot c_3^{x_i^3} \cdot \ldots \cdot c_{t-1}^{x_i^{t-1}} = \\ &= (g^s) \cdot (g^{a_1})^{x_i} \cdot (g^{a_2})^{x_i^2} \cdot (g^{a_3})^{x_i^3} \cdot \ldots \cdot (g^{a_{t-1}})^{x_i^{t-1}} = \\ &= g^{s + a_1x_i + a_2x_i^2 + a_3x_i^3 + \ldots + a_{t-1}x_i^{t-1}} = \\ &= g^{p(x_i)} \\ \end{split}\]
Notice that in the polynomial we have re-constructed the value of the polynomial at the point \(x_i\) without actually knowing the value. Indeed, we can perform this computation even before the \(i\) -th pary decides to reveal his share. When the \(i\) party finally reveals his share \((x_i, y_i)\), I can just check if the value previously computed matches with the \(y_i\) given, that is, if
\[g^{y_i} = g^{p(x_i)} \mod p\]
3 Commitment
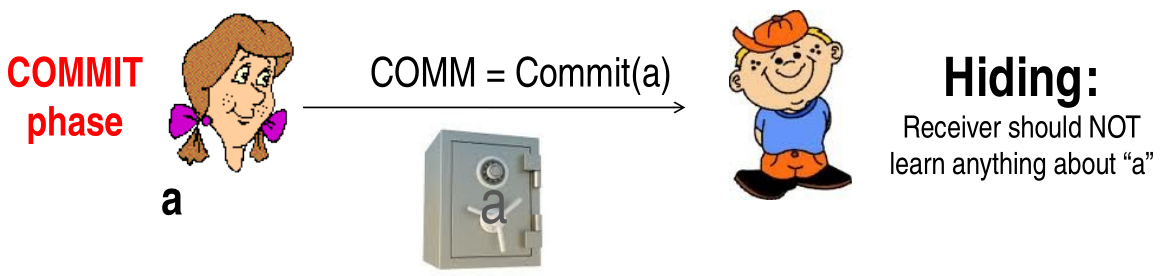
Let's assume that we have a party that knows a private value \(a\). A commiment protocol is composed of two phases:
COMMIT phase: In this phase the party holding the private value \(a\) sends to the other party a value obtained as a function of \(a\). This function should have the hiding property, meaning that by looking at the transformed value no information about the original value should be obtained.
REVEAL phase: In this second phase the party reveals the private value \(a\) as well as give the other party a verification key to make sure the other party is able to understand whether the commitment value received previously is actually linked to the private value \(a\). This second phase must have a binding property, meaning that commitment can only open to the private value \(a\).
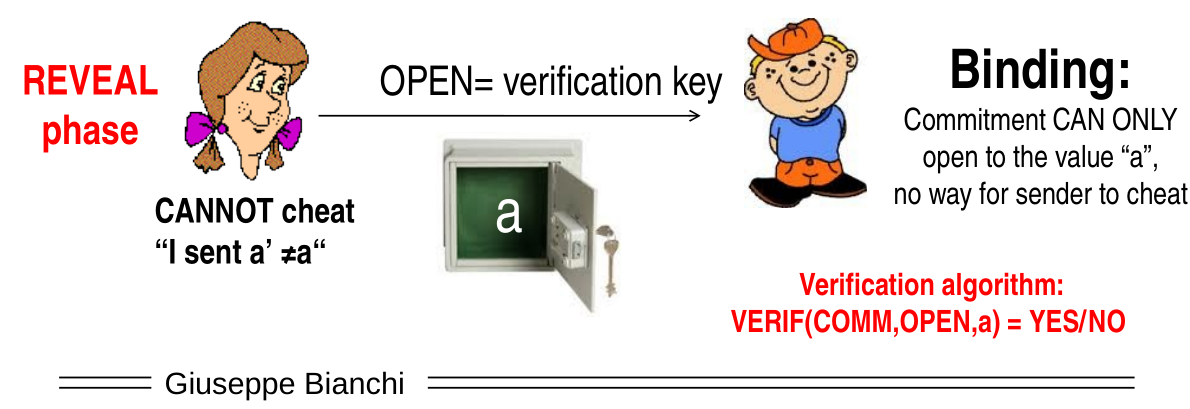
The verification algorithms looks as follows
\[\text{VERIC}(\text{COMM}, \,\, \text{OPEN}, \,\, a) = \text{YES/NO}\]
3.1 Examples
We can have various different commitments. For each one of them we have to understand how much they are hiding and how much they are binding. For example.
Feldman commitment: Given by the following transformation
\[x \to g^x \mod p\]
this commitment is only computationally hiding, because given \(c = g^x \mod p\) it is computationally bounded to get back \(x\), and thus with enough computationally power you can actually break it.
In terms of binding instead this scheme is perfectly binding, because the sender cannot find any other \(x'\) such that \(g^{x'} = c\) where \(x'\) is larger than the group order. This result doesn't depend on computationally power.
Hash commitment: Given by the following transformation, where \(H(\cdot)\) is an hash function.
\[x \to H(x)\]
This commitment is computationally hiding, since with sufficient power you can get back the original value \(x\).
This commitment is also computationally binding, because with sufficient power you can find a new value \(x'\) such that it creates a collsion, that is such that \(H(x') = H(x)\).
Thus an hash function is a bad commitment value.
Observation 1: It is actually impossible to have a commitment scheme that is both perfectly hiding and perfectly binding.
Observation 2: When a scheme such as \(g^x \mod p\) is computationally hiding you need to look at two things:
That \(p\) is large enough.
That \(x\) is large enough in the same order of \(p\).
4 Pedersen Commitment
Remember that the Feldman commitment works because \(g^a \mod p\) is an homomorphic commitment of \(a\), meaning that
\[\text{Commit}(a + b) = \text{Commit}(a) \cdot \text{Commit}(b)\]
The Pedersen commitment is the opposite of the Feldamn commitment, meaning that it is perfectly hiding but only computationally binding but it is still a homomorphic commitment. This scheme was found by Pedersen in 1991, and it is used in several other schemes such as group signatures, ring signatures.
The idea is the following: two bases are publicly given, \(g\) and \(h\). When I ask you to commit you generate a random value \(r\) and give me the following
\[\text{Commit}(a; r) = g^{a} \cdot h^r \mod p\]
Notice that this commit is homomorphic because of the following
\[\begin{split} \text{Commit}(a + b \,\,;\,\, r_a + r_b) &= g^{a+b} \cdot h^{r_a + r_b} \\ &= g^{a}h^{r_a} \cdot g^{b}h^{r_b} \\ &= \text{Commit}(a, r_a) \cdot \text{Commit}(b, r_b) \\ \end{split}\]
Notice that this commiment is perfectly hiding, because \(c=g^a \cdot h^r \mod p\) may be a commitment for any possible value of \(a\). Formally, for any \(a' \neq a\) we can find a unique \(r'\) such that
\[\text{Commit}(a' \,\,;\,\, r') = g^{a'} h^{r'} = g^a h^r = \text{Commit}(a \,\,;\,\, r)\]
This also means that this commitment is only computationally binding.
4.1 Dealer
In this scheme the dealer does the following:
Generates two random polynomials: where \(s\) is the secret and \(r\) is the random value generated for computing the commitment.
\[\begin{split} f(x) &= s + a_1x + a_2x^2 + \ldots + a_{t-2}x^{t-2} + a_{t-1}x^{t-1} \\ f'(x) &= r + b_1x + b_2x^2 + \ldots + b_{t-2}x^{t-2} + b_{t-1}x^{t-1} \\ \end{split}\]
Distributes the shares: Each party \(i\) then receives a double share \((x_i, y_i, z_i)\)
\[\begin{split} y_i &= f(x_i) = s + a_1x_i + a_2x_i^2 + \ldots + a_{t-1} x_i^{t-1} \\ z_i &= f'(x_i) = r + b_1x_i + b_2x_i^2 + \ldots + b_{t-1} x_i^{t-1} \\ \end{split}\]
Publish the commitments: Finally, you publish all the commitments
\[\begin{split} c_0 &= g^s \cdot h^r \\ c_0 &= g^{a_1} \cdot h^{b_1} \\ &\,\,\,\vdots \\ c_{t-1} &= g^{a_{t-1}} \cdot h^{b_{t-1}} \\ \end{split}\]
Notice that all these commits are perfectly hiding.
4.2 Verifier
When party \(i\) receives shares \((x_i, y_i, z_i)\) it can be verifies \(\mod p\) that
\[ c_0 \cdot c_1^{x_i} \cdot c_2^{x_i^2} \cdot \ldots \cdot c_{t-1}^{x_i^{t-1}} = \ldots = g^{y_i} \cdot h^{z_i}\]