CNS - 38 - Applications of Secret Sharing I
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: (43-tresh-crypt.pdf)
Introduction: In this lecture we continue our talk about secret sharing. We first review some left over things about pedersen scheme, and when we start to look into some interesting applications of secret sharing.
1 Pedersen Scheme
As we have seen in a previous lecture, pedersen commitment works by using two values, \(g\) and \(h\) (both public). In this scheme you commit a value \(a\) using a commitment key \(r\) by computing the expression \(g^a \cdot h^r \mod p\).
This commitment scheme is perfectly hiding, meaning that I can always solve the equality
\[g^{a'}h^{r'} = g^ah^r\]
for any \(a\), that is, when I reveal the value of the commitment \(c = g^ah^r\), this value can commit any possible value \(a\), which means that all values are equiprobably.
1.1 Computationally binding proof
The previous argument also means that this commitment scheme is computationally binding, because to solve that equation above you need to compute \(\log_g h\), which is the well-known DLOG problem. This is shown in the following argument.
Let \(h = g^w\), and assume we know \(a, r\) we are given \(a'\), and we want to look for a value \(r'\) such that
\[\begin{split} g^a h^r = g^{a'}h^{r'} &\implies g^a g^{wr} = g^{a'}g^{wr'} \\ &\implies g^{a + wr} = g^{a' + wr'} \\ &\implies a + wr = a' + wr' \mod q \\ &\implies r' = w^{-1}(a - a' + wr) \\ \end{split}\]
where the prime \(p\) is a strong prime, meaning \(p = 1 + 2q\). Notice that to compute such \(r'\) we only need to compute the value \(w\), which, by definition, is
\[h = g^w \iff w = \log_g h\]
\[\tag*{$\checkmark$}\]
1.2 Dealer
The main idea of pedersen scheme is to have two polynomials: one that hides the secret \((s)\) and one that hides the verification key \((r)\). These are computed modulus \(q\), where \(p = 2q + 1\) is a strong prime.
\[\begin{split} f(x) &= s + a_1x + a_2x^2 + \ldots + a_{t-2}x^{t-2} + a_{t-1}x^{t-1} \\ g(x) &= r + b_1x + b_2x^2 + \ldots + b_{t-2}x^{t-2} + b_{t-1}x^{t-1} \\ \end{split}\]
to each party \(i\) is then given a double share \((x_i, y_i, z_i)\)
\[\begin{split} y_i &= f(x_i) = s + a_1x_i + a_2x_i^2 + \ldots + a_{t-1}x_i^{t-1} \\ z_i &= f'(x_i) = r + b_1x_i + b_2x_i^2 + \ldots + b_{t-1}x_i^{t-1} \\ \end{split}\]
and then the commitments are published, these time using a generator \(g\) modulus \(p\).
\[\begin{cases} c_0 = g^s h^r \\ c_1 = g^{a_1} h^b_1 \\ \;\;\; \vdots \\ c_{t-1} = g^{a_{t-1}} h^{b_{t-1}} \\ \end{cases}\]
1.3 Verifier
To verify that the party \(i\) has given the correct share, one can simply do the following check working modulus \(p\).
\[c_0 \cdot c_1^{x_i} \cdot c_2^{x_i^2} \cdot \ldots \cdot c_{t-1}^{x_i^{t-1}} = \ldots = g^{y_i}h^{z_i}\]
2 DKG Scheme
Suppose that we want to generate a public value \(g^x \mod p\) that hides a corresponding private value \(x\). To generate such pair you typically start from the private key \((x)\) and then you compute the corresponding public key \((g^x \mod p)\). Is this generally required? Or, said in another way, can we come up with a scheme at the end of the which we have a public key \(h\) known by all, and nobody knows the private key \(x\), but with the ability to reconstruct the private key at any time we want to?
Observation: This type of issue is very important to our everyday life, because at the moment the European Commission wants to create trapdoors, that is, they think that encryption is also a problem (Security through encryption and security despite encryption). The crypto community came together and signed the following document Open Letter. Instead of making all crypto weaker, the idea is to have schemes which allow the creation of specific trapdoors.
2.1 The Problem
Many cryptosystems are Dlog-based, meaning that they use as a public key a value \(g^x \mod p\), where \(x\) is the corresponding private key. Our problem is then the following: can we generate a pair \((\text{Pub}_k, \text{Priv}_k)\) such that all know \(\text{Pub}_k\) but nobody knows \(\text{Priv}_k\)?
This is useful when:
The private key needs only to be revealed later on.
The private key is never released, but functions of it are needed.
2.2 The Answer
This problem can be solved, and the schemes that solve this problem are called Distributed Key Generation schemes (DKG schemes). They are fully distributed and require no authority or trusted thirt parties (TTPs).
The basic solution was developed by Pedersen in 1991 as a "simple" application of the secret sharing techniques we have seen previously. The original approach was then improved by Gennaro++.
2.3 Example
Let us now see an explicit example of the original Pedersen scheme for DKG. Consider a \((3, 4)\) scheme, where we have \(4\) parties and we want to distribute a public key \(g^s\) such that nobody knows the secret key \(s\), but also such that if \(3\) or more parties get together they are able to reconstruct the secret \(s\). The scheme works as follows:
Step 1: Each party indipendently generates a random secret \(a_{0, i}\).
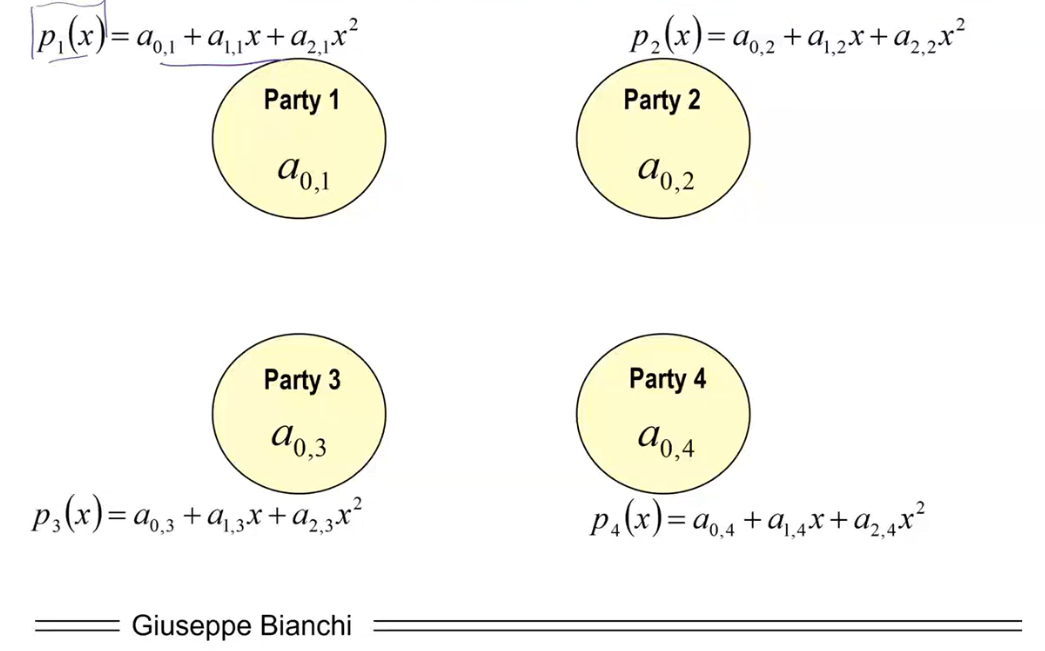
Step 2: Each party generates a random polynomial of degree \((t-1)\) with known term \(a_{0, i}\).
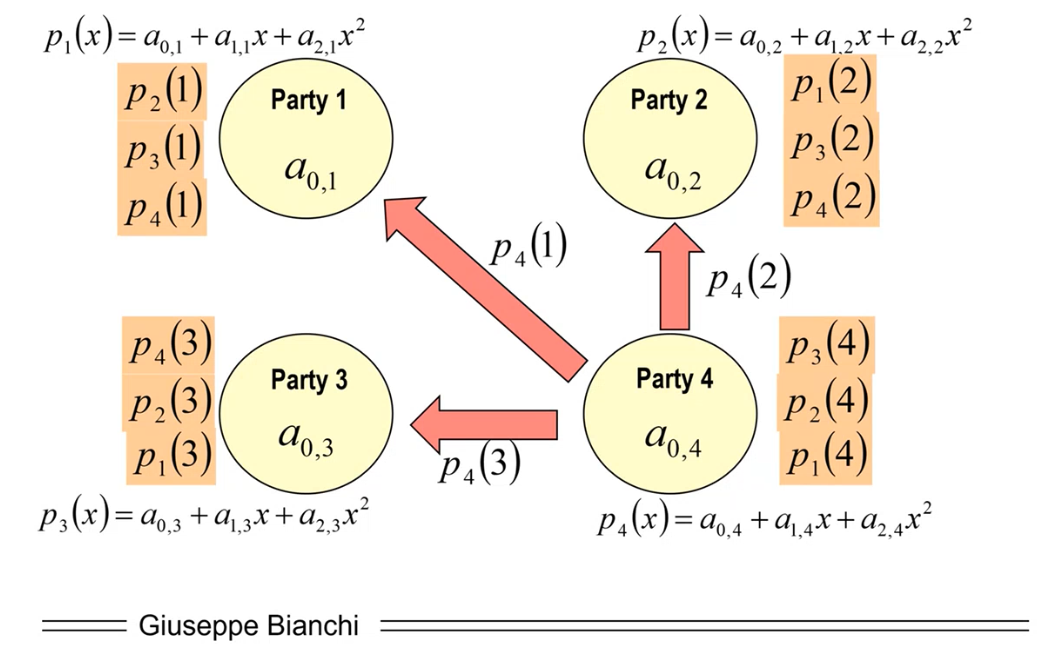
Step 3: Each party securely exchange a share of their own polynomial with every other party.
Step 4: Each party computes "self" share
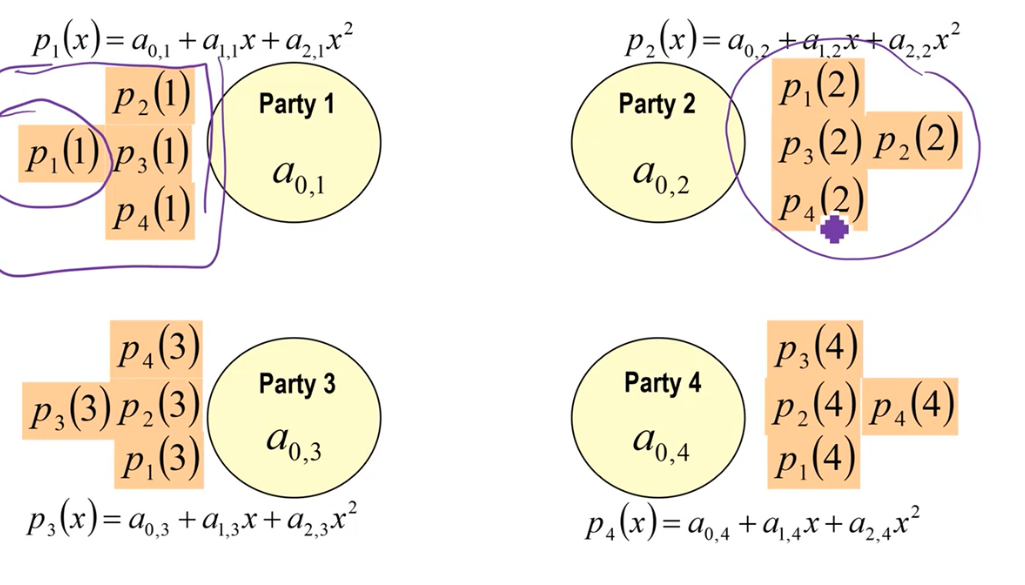
Step 5: Each party computes a "full" share by taking the sum of all the shares received and computed so far.
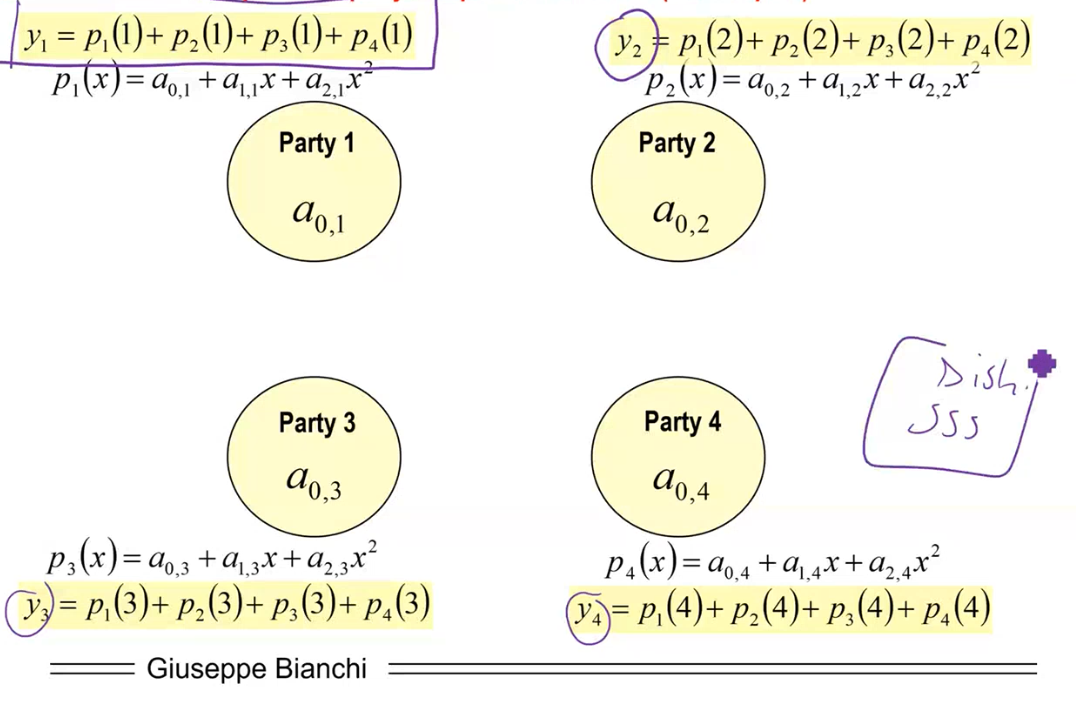
Step 6: Finally, each party broadcasts a commitment value for \(a_{0,i}\). That is, they broadcast the value \(g^{a_{0, i}}\).
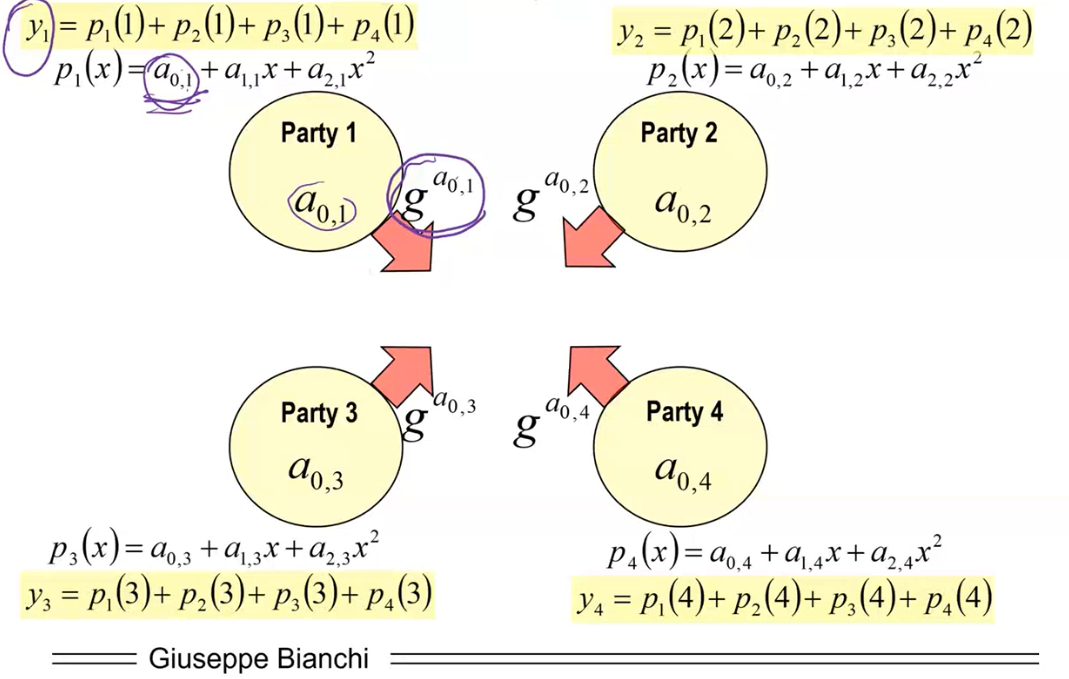
At the end of the day with all these steps we have built a random polynomial \(P(x)\) with \(s\) as the known term.
\[\begin{split} P(x) &= p_1(x) + p_2(x) + p_3(x) + p_4(x) \\ &= a_{0, 1} + a_{1,1}x + a_{2,1}x^2 \\ &\;\;\;\;\;+ a_{0, 2} + a_{1,2}x + a_{2,2}x^2 \\ &\;\;\;\;\;+ a_{0, 3} + a_{1,3}x + a_{2,3}x^2 \\ &\;\;\;\;\;+ a_{0, 4} + a_{1,4}x + a_{2,4}x^2 \\ &= s + \alpha_1 x + \alpha_2 x^2 \end{split}\]
where,
\[\begin{split} s &= a_{0, 1} + a_{0, 2} + a_{0, 3} + a_{0, 4} \\ \alpha_1 &= a_{1, 1} + a_{1, 2} + a_{1, 3} + a_{1, 4} \\ \alpha_2 &= a_{2, 1} + a_{2, 2} + a_{2, 3} + a_{2, 4} \\ \end{split}\]
Notice that the term \(s\) (the private key) is unknown to all, but using the commitment values everyone can compute the relative public key \(g^s\) as follows
\[g^{a_{0, 1}} \cdot g^{a_{0, 2}} \cdot g^{a_{0, 3}} \cdot g^{a_{0, 4}} = g^{a_{0, 1} + a_{0, 2} + a_{0, 3} + a_{0, 4}} = g^s\]
3 Applications of Secret Sharing
The secret sharing techniques we have seen so far can be applied in numerous situations such as:
Threshold encryption
Threshold signatures
(monotone) access control policies
Capture resistance
Delegate security functionalities to proxies
An example of such application is the following: consider a private key which holds a Bitcoin account. Typically people think that when using such private key you can only do the following two things:
You either fully entrust a so-called Wallet, which is a third party that manages your bitcoin account;
You take full responsibility of your bitcoin account, and you have to manage everything on your own.
The truth of the matter is that secret sharing techniques open up the possibility for the following third option: you create a \((2, 3)\) scheme in which you split your private key between \(3\) entities: your PC, the third party (like Coinbase), and a USB in a secret vault. With this approach you get the benefit of working with platforms like Coinbase, but at the same time Coinbase by itself cannot reconstruct the private key on his own, and also, even if Coinbase decides to run away, you can reconstruct your private key using the share left on the protected USB drive.
4 ElGamal Cryptosystem
As a first application of secret sharing lets start from threhsolh encryption, which is used in an encryption scheme called ElGamal, which is a public key encryption scheme based on the DLOG problem. Remember that the other public key crypto scheme we have used so far was the RSA sheme, which is based on the factoring problem. The other thing we have seen that uses the DLOG problem was the Diffie-Hellman key exchange, which is not a full crypto system.
In 1985 ElGamal discovered, in a "columbus egg" fashion, that DH could also be used for encryption. The ElGamal system has the following properties:
Asymmetric cryptosystem
Inspired by DH
Probabilistic cipher
This scheme uses a large prime \(p\) and a group generator \(g\). All the operations are done \(\mod p\), the private key is a value \(s\) and the public key is the value \(h = g^s\). Finally, whenever we want to generate something we first have to generate a random value \(r\). This value is ephemeral, meaning that for each text we want to encrypt a different random value has to be generated.
The encryption operation to encrypt a message \(m\) is the following: we first generate a random value \(r\), then we compute the compute and send the values \(g^r\) and \(m \cdot h^r\).
\[m \overset{\text{enc}}{\longrightarrow} (g^r, m \cdot h^r)\]
When the person of interest receives the encrypted message \((g^r, m \cdot h^r)\) to decrypt it the following operation is performed:
\[(g^r, m \cdot h^r) \overset{\text{dec}}{\longrightarrow} m \cdot h^r \cdot ((g^{r})^{s})^{-1}\]
Notice by computing such value we get the original message back, since
\[m \cdot h^r \cdot ((g^{r})^{s})^{-1} = \frac{m \cdot h^r}{g^{rs}} = \frac{m \cdot g^{sr}}{g^{rs}} = m\]
the basic idea of this system is that \(h^r = (g^s)^r\), and to compute \(g^{sr}\) I can either compute \((g^s)^r\) or I can compute \((g^r)^s\). This is exactly the idea behind the Diffie-Hellman key exchange. Once I have \(g^{sr}\) I can easily compute its inverse, and thus get back the original message \(m\).
5 Threhsold Cryptography
The idea of threshold encryption is to encrypt something to a group of people such that the text can be decrypted only if \(t\) or more people get together. Let us then see how to implement such scheme using the Elgamal cryptosystem.
5.1 Elgamal Treshold
The first idea to implement such type of encryption could be to simply distribute shares of the private key \(s\) and then reconstruct \(s\) when decryption is needed. The problem with this idea is that the moment we reconstruct the private key, every party involved will be able to decrypt subsequente messages on their own. Thus this approach would only work once.
5.1.1 Towards the Solution
Notice that when using ElGamal crypto system when we encrypt two different messages \(m_1, m_2\) we do the following
\[\begin{split} m_1 &\overset{\text{enc}}{\longrightarrow} (g^{r_1}, m_1 \cdot h^{r_1}) \\ m_2 &\overset{\text{enc}}{\longrightarrow} (g^{r_2}, m_1 \cdot h^{r_2}) \end{split}\]
then, when we decrypt, we do the following
\[\begin{split} (g^{r_1}, m_1 \cdot h^{r_1}) &\overset{\text{dec}}{\longrightarrow} \frac{m_1 \cdot h^{r_1}}{(g^{r_1})^s} = m_1 \\ (g^{r_2}, m_2 \cdot h^{r_2}) &\overset{\text{dec}}{\longrightarrow} \frac{m_2 \cdot h^{r_2}}{(g^{r_2})^s} = m_2 \\ \end{split}\]
The idea then is that if we want to decrypt only \(m_1\) and not \(m_2\) we don't have to reconstruct \(s\), but rather we have to reconstruct \(g^{r_1 s}\), which is the quantitiy that is specifically used to decrypt \(m_1\).
Notice also that since \(A^{x_1} \cdot A^{x_2} = A^{x_1 + x_2}\), whenever we need to reconstruct a sum in the exponent we only need to multiply the terms together.
The idea is then to generate the usual polynomial
\[p(x) = s + a_1x + a_2x^2 + \ldots + a_{t-2}x^{t-2} + a_{t-1}x^{t-1}\]
then every party involved will have a share \(y_i = p(x_i)\) and to reconstruct \(s\) the usual lagrange interpolation can be computed
\[s = \sum_{\text{shares} x_i} y_i \Lambda_{x_i}\]
where \(\Lambda_{x_i}\) is the lagrange polynomial computed at \(x = 0\)
\[\Lambda_{x_i} = \Lambda_{x_i}(0) = \prod\limits_{\text{shares } x_k \neq x_i} \frac{x_k}{x_i - x_k}\]
notice that this reconstruction can also be done at the exponent, since for the basic law of the exponents we have mentioned we have
\[\prod A^{y_i \Lambda_{x_i}} = A^{\sum x_i \Lambda_{x_i}} = A^s\]
5.1.2 The Solution
The final solution of the problem can be then be formalized as follows:
Each party owns one share \((x_i, y_i)\) with \(y_i = p(x_i)\)
Before starting each party computes the various lagrange coefficients
\[\Lambda_{x_i} = \prod\limits_{\text{shares } x_k \neq x_i} \frac{-x_k}{x_i - x_k}\]
A message \(m\) is then encryped as \((g^r, m \cdot h^r)\), and each party wants to decrypt this message without actually reconstructing \(s\).
To do this from the ciphertext \((g^r, m \cdot h^r)\) each party extracts the value \(g^r\) and computes the exponent share \((g^r)^{y_i \Lambda_{x_i}}\).
Given a sufficient number of shares then the decryption key \(g^{rs}\) can be reconstructed as follows
\[\prod (g^r)^{y_i \Lambda_{x_i}} = (g^r)^{\sum y_i \Lambda_{x_i}} = (g^r)^s = g^{rs}\]
Notice that this key only allows each party to decrypt the specific message \(m_1\), and not any other message.
Once the value \(g^{rs}\) is reconstructed I can decrypt the ciphertext and get the original message back as follows
\[\frac{m h^r}{g^{rs}} = \frac{m \cdot g^{sr}}{g^{rs}} = m\]
With this scheme nobody can reconstruct the original private key \(s\), because party \(i\) does not reveal his/her share \(i\), but only the value \((g^r)^{y_i \Lambda_{x_i}}\).