CNS - 39 - Applications of Secret Sharing II
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: (43-tresh-crypt.pdf)
Introduction: In this lecture we see futher applications to secret sharing such as how to implement threshold signature using RSA.
1 Why DLOG cryptosystems are better
In TLS we preferred DH instead of RSA because the former guarantees perfect forward secrecy. In general DLOG cryptosystems are preferred instead of RSA, because they ovver an easier implementation over Elliptic Curves Groups.
Observation: Elliptic curve cryptography is preferred over RSA because it scales much better, as is shown in the following table in which the security of three different cryptosystems is measured in terms of bits used.
\[\begin{array}{c | c | c} \text{Symm key} & \text{Modulus Size} & \text{Elliptic Curve}\\ \hline 80 \text{ bits} & 1024 \text{ bits} & 163 \text{ bits} \\ 128 \text{ bits} & 3072 \text{ bits} & 283 \text{ bits} \\ 256 \text{ bits} & 15360 \text{ bits} & 571 \text{ bits} \\ \end{array}\]
2 Hybrid Ciphers
Remember that we can have a "hybrid" usage of public/private key cryptosystems and of symmetric key cryptosystems.
For example, consider a situation where you want to send an e-mail to someone, but that someone is now offline, and thus you cannot use TLS and other protocols that require the presence of the other party. If we encrypt the entire message using the public key of the destination of the message, we incur in the following two problems:
We have to split up the message into different chunks and link those chunks up.
For each chunk we have to compute the RSA encryption, which takes 4-5 orders of magnitude more than a simple symmetric algorithm.
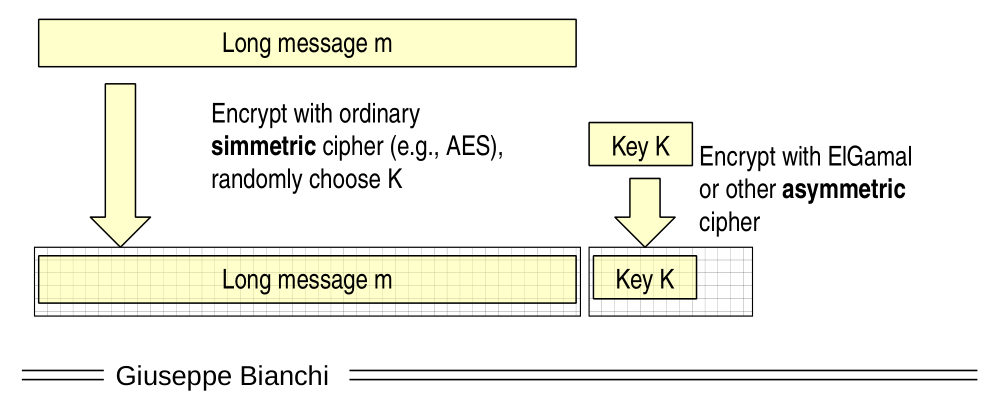
To fix these problems the idea is to use a hybryd encryption, which is done as follows:
First we generate a random key \(k\) and we encrypt the message with the choosen key.
Then we encrypt the symmetric key \(k\) with an asymmetric cipher, like ElGamal, or RSA.
2.1 ECIES
Among the asymmetric ciphers the ECIES cipher is an hybrid encryption scheme which is used in the 5G system. It is conceptually similar to El-Gamal, but is still a different system, and it is specifically used to encrypt your identity.
The approach used is the ECIES one, which stands for Elliptic Curve Integrated Encryption Scheme. This scheme is very technical, but the complexity is mainly due to the fact that it is done over an Elliptic Curve Group. In this discussion we will thus skip the technical details and we will see the general idea behind such approach.
The scheme works as follows: in your sim card you have hardcoded the public key of your operator \(g^{\text{HN}}\). When you want to transfer something you generate a random element \(x\) and compute an ephemeral term \(g^x \mod p\). Then, you use an HKDF (see previous lecture for more details) to derive the encryption and integrity keys \(K = \text{HKDF}(g^{\text{HN} \cdot x})\). You can then use a symmetric cipher like AES followed by an HMAC integrity check.
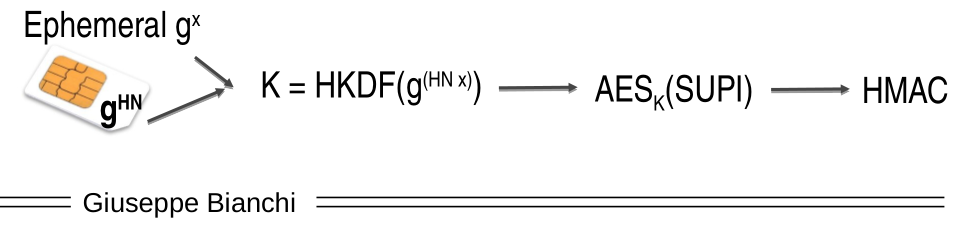
Observation: Notice that the order followed this time was \(\text{ENC} \to \text{MAC}\), which is the correct order. Remember that in TLS the other order was used, and this led to various types of Oracle Padding Attacks.
3 Threshold Signature
The idea of treshhold signature is to let a message to be signed only when at least \(t\) different persons get together. This allows one to place trust in more than a single certificate authority.
3.1 RSA Signature
Remember that in RSA we have two large primes \(p, q\) and the modulus is computed by \(N = pq\). The public key is then \((e, N)\) and the private key is \(d = e^{-1} \mod \Phi(N) = (p-1)(q-1)\).
To then sign a message you compute the following
\[m \longrightarrow (m, H(m)^d)\]
and to verify the signature you check that
\[H(m) = (H(m)^d)^e\]
3.2 Threshold RSA (wrong)
To construct a threshold RSA scheme we proceed as follows: the dealer constructs a polynomial working \(\mod \Phi(N)\)
\[f(x) = d - a_1x + a_2x^2 + \ldots + a_{t-2}x^{t-2} + a_{t-1}x^{t-1}\]
and by using such polynomal gives to party \(i\) the share \((x_i, y_i = f(x_i) \mod \Phi(N))\).
The message to be signed is \(m, H(m)\). The signature share that each party gives is then \(H(m)^{y_i \Lambda_{x_i}} \mod N\). The valid signature is then obtained by multiplying such terms together, to obtain
\[\prod H(m)^{y_i \Lambda_{x_i}} = H(m)^{\sum y_i \Lambda_{x_i}} = H(m)^d\]
WARNING: The approach just described is actually wrong. This is because of the following two problems:
First of all, there is a technical problem: to reconstruct the signature party \(i\) must compute \(H(m)^{y_i \Lambda_{x_i}} \mod N\), where
\[\Lambda_{x_i} = \prod\limits{\text{shares } x_k \neq x_i} \frac{-x_k}{x_i - x_k} = \frac{\alpha_{x_i}}{\beta_{x_i}}\]
and to compute such value you need that \(\beta_{x_i}\) must be coprime with \(\Phi(N)\), which is not a prime number.
But even if we fixed the technical problem, there is a much deeper problem. The real problem is that while the dealer knows \(\Phi(N)\), to compute the various lagrange coefficients one must need to know \(\Phi(N)\). But this information should not be accessible to the various parties involved.
3.3 Threshold RSA (right)
To fix these problems Victor Shoup came up with an article named Pratical Threshold Signatures.
To avoid inverses he used the following idea. assume usual \(x_i = i\) and let \(L\) be the maximum number of players involved. By looking at the Lagrange polynomial denominator we can see that the denominator surely divides \(i!(L-i)!\). Indeed
\[\Lambda_i(x) = \prod\limits_{\text{shares } k \neq i} \frac{x - k}{i - k} = \frac{\text{something}(x)}{(i-1)(i-2) \ldots (i-(i-1))(i - (i+1)) \ldots (i - L)}\]
But remember that the binomial coefficient of \(\binom{L}{i} = L!/(i!(L-i)!)\), and this is an integer value. Which means that the denominator of \(\Lambda_i(x)\) not only divides \(i!(L-i)!\), but it also divides \(L!\). Thus, by multiplying by \(L!\) the Lagrange coefficient we always get an integer
\[\bar{\Lambda}_i(x) := L! \cdot \Lambda_i(x) \implies \bar{\Lambda}_i(x) \text{ is surely integer}\]
The idea is then to compute the signature share as \(H(m)^{y_i \bar{\Lambda}_{x_i}} \mod N\). With this approach we don't need inverses anymore, since Lagrange coefficients are now integers. This also means that we dont need to know the value of \(\Phi(N)\). To re-construct the share then the following value is computed
\[\prod\limits H(m)^{y_i \bar{\Lambda}_{x_i}} = H(m)^{L! \cdot \sum x_i \Lambda_{x_i}} = H(m)^{d \cdot L!} \mod N\]
Notice however that to get the actual signature \(H(m)^d\) we would need to get the \(L!\) rooth, which involves computing inverses. Thus, we still seem to not have solved our original problem. Well, the reality is that we can fix this problem, and to do so we will use, for a good purpose, a well known RSA attack called common modulus attack (discussed in the next section).
In particular the idea is to use a different value, say \(e\), which is coprime with \(L!\) and to compute the value \(H(m)^{de}\). If \(e\) and \(L!\) are coprime, then we can apply the common modulus attack to obtain the message \(H(m)^d\), which is exactly the signature we want. This works as long as \(e\) is a prime number greater than \(L\).
3.3.1 Further Extensions
In 2001 Foque and Stern showed how to apply a Pedersen-type distributed generation to come out with a distributed way to generate strong primes.
3.4 RSA common modulus attack
A well knownattack to the RSA cryptosystem is the so-called common modulus attack. This attack can be performed when two people encrypt the same message \(m\) using two public keys \(e_a\) and \(e_b\) using the same moudlus \(N\) and such that \(\text{GCD}(e_a, e_b) = 1\).
The idea is to use the extended euclidean algorithm to find two values \(r\) and \(s\) such that
\[e_a \cdot r + e_b \cdot s = \text{GCD}(e_a, e_b) = 1\]
In particular, consider the same message encrypted once as \(m^{e_a}\) and once as \(m^{e_b}\). Once we find those \(r\) and \(s\) we can compute the following value
\[(m^{e_a})^r \cdot (m^{e_b})^s = m^{e_a \cdot r + e_b \cdot s} = m^1 = m\]
and thus you have decrypted \(m\). This is why you never want to use the same modulus \(N\) for different public/private key pairs.