CNS - 40 - Applications of Secret Sharing III

Lecture Info

Date: [2020-12-23 mer 11:30]
Lecturer: Giuseppe Bianchi
Slides: (45-mckenzie.pdf)
Introduction: In this lecture we see an example of how to make mobile devices more resilient to capture.

1 Some Statistics

In 2010 a survey on 329 organizations showed that 86400 laptop were lost, for a totaly value of 2.1B $.

Most of the time its not the laptop itself that is the valuable thing lost, but rather the data contained in it.

2 Capture Resilient Device

The idea of a capture resilient device is of a device that cannot be used by anyone else other than the rightful owner. In the following discussion we will assume that in the "core" of the device there is a secret key.

Possible security approaches to protect the device are:

Store secret in tamper-proof hardware box.
Lock/Unlock key via passwd.
Dynamically download key from network repository.

Notice that in these three approaches we must assume something in terms of security, which is not ideal.

2.1 MacKenzie + Reiter, 2003

The approach found out by MacKenzie and Reiter assumes that the device is always connected when used, and it involves a "capture-protection server" in the network, whose purpose is to confirm that the device remains in owner's possession before permitting usage of the key. The key point is that the capture-protection server does not need to be trusted.

To do this there are two different approaches:

A basic one, involving standard crypto used in a clever manner.
An extended one, which uses a $(2, 2)$ secret sharing scheme.

3 Basic Scenario

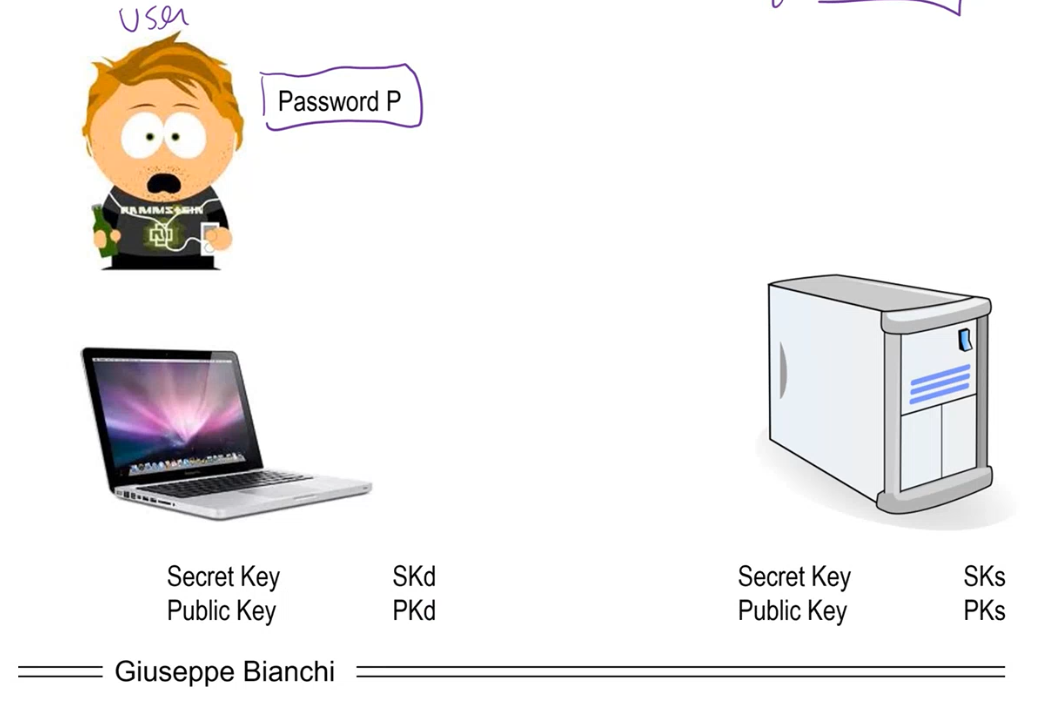
The basic scenario studied by MacKenzie and Reiter is shown below:

3.1 Basic Solution

The basic solution was robust against any of the three attacks if done individually (meaning max $1$ at a time), and also to the following couples of attacks:

Server cracked and pasword known
Device and server cracked.

This means that the basic solution is not robust against device being cracked and a password being known.

Note also that the basic solution does not use any fancy crypto. Before explaining the solution let us assume that the device has access to the network.

The main idea is to share information through the usage of tickets so that you can decrypt it only later on in time. In particular we assume that there is a single device key, which is necessary to use the device. This device key is encrypted, and it can only be decrypted via cooperation with the server.

3.1.1 Device Initialization

At the start the device is initialized as is shown in the following scheme

in more detail:

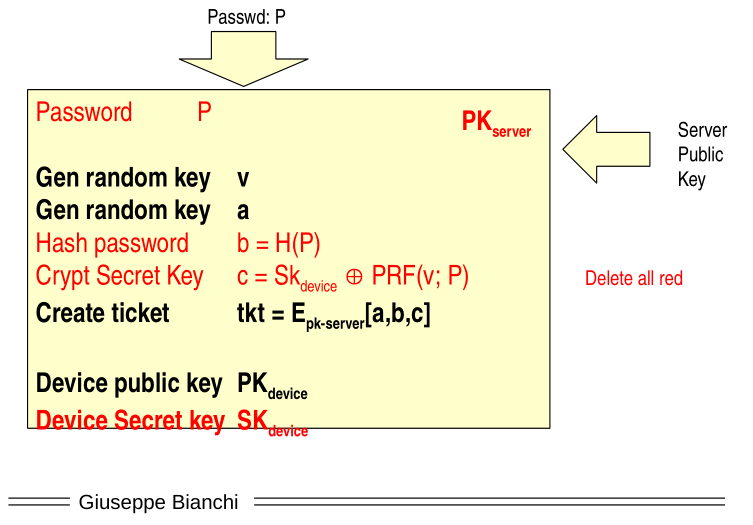
The password of the user $P$ as well as the public key of the server $\text{PK}_{\text{server}}$ are sent to the device.
The device generates two random keys $v$ and $a$.
The password is hashed to obtian $b = H(P)$.
The secret key is encrypted as follows

\[c = \text{Sk}_{\text{device}} \mathbin{\oplus} \text{PRF}(v; P)\]

where the keystream is generated starting from the key $v$ and from the seed $P$. This means that the secret of the device is protected both from the value $v$ as well as the password of the client $P$.
Finally, the values $a$, $b$ and $c$ are encrypted using the public key of the server to create a ticket $\text{tkt}$.

At the end of the process the password $P$, the hashed password $b$, the encrypted device key $c$ as well as the device secret key and the server public key, are deleted from the memory of the device. (in the scheme above all the red lines). This means that when an attacker steals your device, he only finds the two random keys $v$ and $a$, the ticket $\text{tk}$, and the public key of the device.

Notice also that when the server decrypts the ticket, it is still not able to read the secret key of the device, but it is only able to read the encrypted version of the secret key.

3.1.2 Key Retrieval

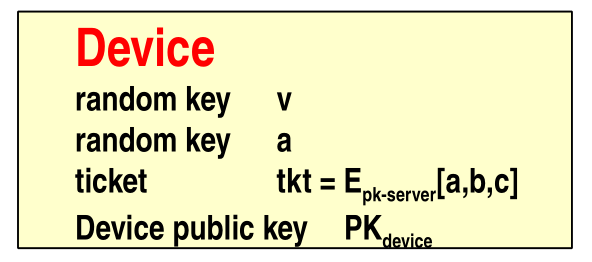
Let us now assume that we are online and that we want to unlock our device. The device by itself can only access the following stuff

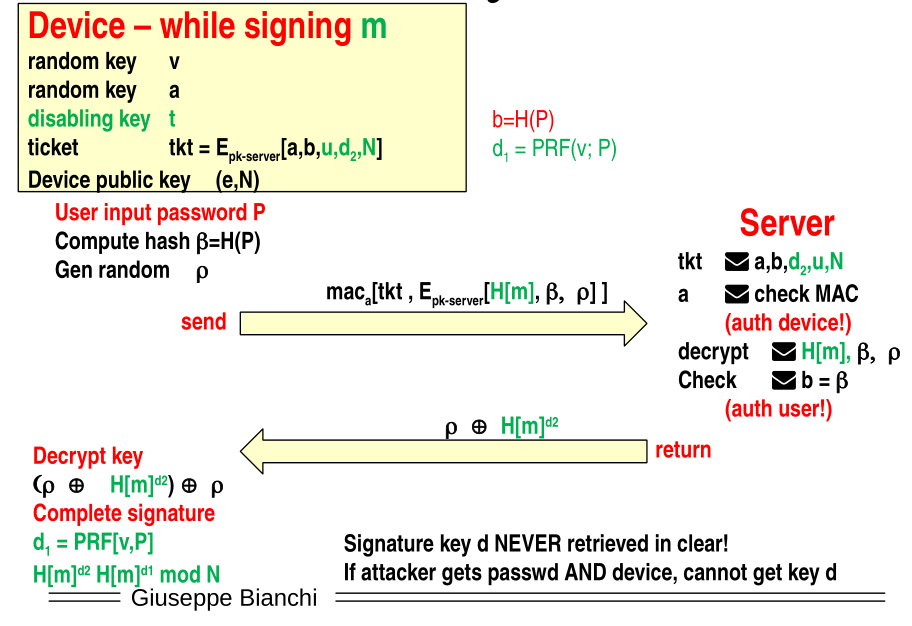
Tu unlock the device the following steps have to take place:

The user inputs the password $P$ and device computes the hash of the password $\beta = H(P)$ and generates a random keystream $\rho$, which will be used by the server to send securely the value $c$.
The devive then sends to the server the tkt as well as the hash of the password encrypted with the public key of the server and the generated keystream. This message is also signed using the key $a$.
When the server receives the message, it opens the ticket, it checks if the signature is correct using the parameter $a$, and then it decrypts the hash of the password and it checks that the decrypted hash of the password corresponds to the $b$ present in the decrypted ticket. In this step thus the server authenticates both the user and the device.
If the user is authenticated correctly, then the server returns the encrypted version of the device secret key $c$ using the keystream $\rho$ as a symmetric cipher.
Once the device receives $\rho \mathbin{\oplus} c$ it can dynamically recompute the secret key of the device as follows

\[(\rho \mathbin{\oplus} c) \mathbin{\oplus} \rho \mathbin{\oplus} \text{PRF}[v, P] \longrightarrow \text{Sk}_{\text{device}}\]

3.1.3 Attacks

Let us now view different attacks scenario and discuss for each one of them a possible solution:

Server cracked AND password known: In this case the security relies on the fact that the key $v$ is in the device, and since the secret key is encrypted with $\text{PRF}[v, P]$, then it cannot be obtained.
Device cracked/stolen: If the device is stolen or cracked, then the attacker can access the random key $v$. Having said that, to actually decrypt the secret key of the device, the attacker also needs to know the password. Notice however that to brute-force the password the attacker cannot do an offline attack, because the hash of the password is not stored on the device, but is rather stored on the server. Therefore an online dictionary attack has to be performed.
Device and Server cracked: In this case I'm protected but only by offline dictionary attacks.

3.2 Better Solution

Notice that the scheme we have previously described does not work if the device is cracked and the password is stolen. In this case an attacker is easily able to decrypt the secret key of the device.

The idea is to improve this scheme by using the secret sharing techniques we have previously discussed and by making sure that the secret key is never disclosed to anyone, even to the device itself.

3.2.1 Secret Sharing (2, 2) for RSA

Notice that if we want a simply sharing scheme $(2, 2)$ we don't need to mess around with the solution discovered by Victor Shoup.

In particular, let $n = p \cdot q$ and let $d$ be the secret key. Then you generate a random value $d_1$ and you compute $d_2 = d - d_1 \mod \phi(n)$. The first share will then be $d_1$, while the second one will be $d_2$. When you want to sign a message you first sign it using both shares, and then you multiply the signed messages to obtain the proper signature

\[H(m)^{d_1} \cdot H(m)^{d_2} = H(m)^{d_1 + d_2} = H(m)^{d_1 + d - d_1} = H(m)^d \mod n\]

3.2.2 Device initialization

The new initialization is then the following

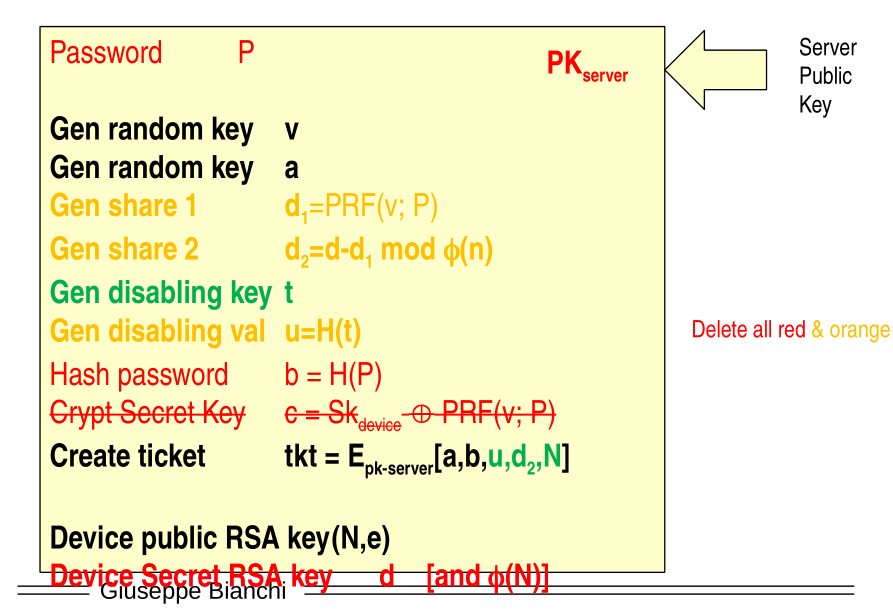
As we can see, the scheme is similar to the previous one, but with the following differences:

Now the device secret key is never encrypted and sent to the server. What is instead sent to the server is the values $a$ and $b$ for the authentication of both the device and the user, as well as the values $d_2$, $N$ and $u$.
The first share $d_1$ is not generated randomly, but rather through a PRF using the random key $v$ and the password $P$. Notice that this choice moves the security of the system from a theoretical information security to a computational security, but at the same time to reconstruct the share both the knowledge of the password as well as of the device are needed.

3.2.3 Key retrieval

Whenever we want to sign a message we have to ask the server for its share. The scheme is the following