CNS - 41 - Linear Secret Sharing
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: (44-lsss.pdf)
Introduction: In this lecture we will see that the concept of secret sharing is much more general than the techniques we have seen so far.
1 Revisiting Schamir Scheme
Let us review how shamir secret sharing scheme works. This time however we will change the presentation, that is we will interpret the various components using concepts taken from linear algebra, such as matices and vectors.
In the scheme we had originally presented we had a secret \(s\) that we wanted to share, and the \(i\) share was the point of a polynomial evaluated at a given \(x_i\) value
\[y_i = s + a_1x_i + a_2x_i^2 + \ldots + a_{t-2}x_i^{t-2} + a_{t-1}x_i^{t-1}\]
Now consider a vector interpretation of the share \((x_i, y_i)\). In this interpretation the share is obtained with a scalar product of the following two vectors: the vector containing powers of \(x_i\) and the vector containg the secret \(s\) random values \(a_i\).
\[y_i = \begin{bmatrix}1 & x_i & x_i^2 & \cdots & x_i^{t-2} & x_i^{t-1} \end{bmatrix} \cdot \begin{bmatrix}s & a_1 & a_2 & \cdots & a_{t-2} & a_{t-1} \end{bmatrix}\]
Since the coefficients are random lets us called them \(r_i\) instead of \(a_i\). Therefore we get
\[y_i = \begin{bmatrix}1 & x_i & x_i^2 & \cdots & x_i^{t-2} & x_i^{t-1} \end{bmatrix} \cdot \begin{bmatrix}s & r_1 & r_2 & \cdots & r_{t-2} & r_{t-1} \end{bmatrix}\]
1.1 As Matrix Form
Let us now write shamir scheme in a matrix form, that is as
\[Ax = b\]
where,
\(A\) is a given matrix of size \(n \times t\).
\(x\) is a vector of size \(t\) made of the secret and the random values \(r_i\).
\(b\) is another vector, this time of size \(n\), containing the resulting shares.
Example (3, 4): For example, in a three out of four secret sharing, we get the following
\[\begin{bmatrix} 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \\ 1 & x_3 & x_3^2 \\ 1 & x_4 & x_4^2 \\ \end{bmatrix} \cdot \begin{bmatrix} s \\ r_1 \\ r_2 \\ \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ \end{bmatrix}\]
Notice that the matrix we obtained is known as the Vandermonde matrix. The idea which will be explored in this lecture is that, by changing the matrix \(A\), we can get different types of secret sharing schemes, which are known as linear secret sharing schemes, in acrynonim LSSS.
1.1.1 Reconstructing the Secret
To reconstruct the share we have to solve the following linear system, where the unknown is the secret \(s\) and the two coefficients of the polynomial \(r_1, r_2\).
\[\begin{bmatrix} 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \\ 1 & x_4 & x_4^2 \\ \end{bmatrix} \cdot \begin{bmatrix} s \\ r_1 \\ r_2 \\ \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ y_4 \\ \end{bmatrix}\]
we know from linear algebra that the determinant of the matrix is \(\neq 0\), which means that the matrix is invertible, and thus the system has at least a solution (or maybe a single solution, I don't remember at the moment). Thus our solution is given by computing
\[\begin{bmatrix} s \\ r_1 \\ r_2 \\ \end{bmatrix} = \begin{bmatrix} 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \\ 1 & x_4 & x_4^2 \\ \end{bmatrix}^{-1} \cdot \begin{bmatrix} y_1 \\ y_2 \\ y_4 \\ \end{bmatrix}\]
Notice that now we can reconstruct the secret by solving a linear system. While this prodecude is different from the one we used before (Lagrange interpolation), the final result is the same, because when we look at the inverse matrix we get the following
\[\begin{bmatrix} 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \\ 1 & x_4 & x_4^2 \\ \end{bmatrix}^{-1} = \begin{bmatrix} \frac{x_2 x_4}{(x_1 - x_2)(x_1 - x_4)} & \frac{x_1 x_4}{(x_2 - x_1)(x_2 - x_4)} & \frac{x_1 x_2}{(x_4 - x_1)(x_4 - x_2)} \\ \ldots & \ldots & \ldots \\ \ldots & \ldots & \ldots \\ \end{bmatrix} = \begin{bmatrix} \Lambda_1(0) & \Lambda_2(0) & \Lambda_4(0) \\ \ldots & \ldots & \ldots \\ \ldots & \ldots & \ldots \\ \end{bmatrix}\]
and so the reconstruction formula is exactly the lagrange interpolation formula
\[\begin{split} s &= y_1 \cdot \frac{x_2 x_4}{(x_1 - x_2)(x_1 - x_4)} + y_2 \cdot \frac{x_1 x_4}{(x_2 - x_1)(x_2 - x_4)} + y_4 \cdot \frac{x_1 x_2}{(x_4 - x_1)(x_4 - x_2)} \\ &= y_1 \cdot \Lambda_1(0) + y2 \cdot \Lambda_2(0) + y_4 \cdot \Lambda_4(0) \end{split}\]
1.2 As Span problem
Let us now offer an alternative interpretation of the scheme presented so far by using the so-called span problem. In particular consider the following scheme
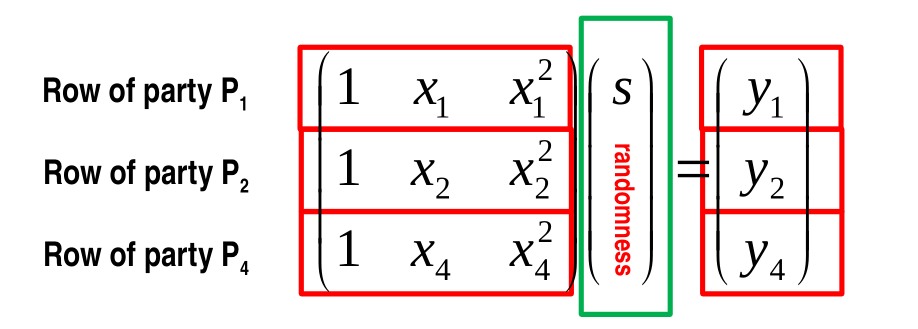
Note that the linear combinations of the row vectors of the matrix \((v_1, v_2, v_3)\) \(A\) form a 3d space. That is, by changing coeficients \(c_1, c_2\) and \(c_3\) we can compute the following expression
\[c_1 \cdot \begin{bmatrix} 1 \\ x_1 \\ x_1^2 \\ \end{bmatrix} + c_2 \cdot \begin{bmatrix} 1 \\ x_2 \\ x_2^2 \\ \end{bmatrix} + c_3 \cdot \begin{bmatrix} 1 \\ x_4 \\ x_4^2 \\ \end{bmatrix}\]
and get a point in a 3D space. In this space we are particulary interested in one point, the point \(\begin{bmatrix} 1 & 0 & 0\end{bmatrix}\). Notice that if such point in contained in the space spanned by the three vectors, then there exist three values \(c_1, c_2\) and \(c_3\) such that
\[c_1 \cdot \begin{bmatrix} 1 \\ x_1 \\ x_1^2 \\ \end{bmatrix} + c_2 \cdot \begin{bmatrix} 1 \\ x_2 \\ x_2^2 \\ \end{bmatrix} + c_3 \cdot \begin{bmatrix} 1 \\ x_4 \\ x_4^2 \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix}\]
To find these three coefficients we have to solve the following linear system
\[\begin{bmatrix} 1 & 1 & 1 \\ x_1 & x_2 & x_4 \\ x_1^2 & x_2^2 & x_4^2 \\ \end{bmatrix} \cdot \begin{bmatrix} c_1 \\ c_2 \\ c_3 \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix}\]
Notice that the solution of such system are exactly the lagrange coefficients of before, that is
\[\begin{split} c_1 = \frac{x_2 x_4}{(x_1 - x_2)(x_1 - x_4)} = \Lambda_1(0) \\ \\ c_2 = \frac{x_1 x_4}{(x_2 - x_1)(x_2 - x_4)} = \Lambda_2(0) \\ \\ c_3 = \frac{x_1 x_2}{(x_4 - x_1)(x_4 - x_2)} = \Lambda_4(0) \\ \\ \end{split}\]
Notice that this result is not a big surprise, because of the following: if we assume that \(c_1\), \(c_2\) and \(c_3\) are the solution to the previous linear system, then we get
\[\begin{split} \Bigg(&c_1 \cdot \begin{bmatrix} 1 & x_1 & x_1^2 \end{bmatrix} + c_2 \cdot \begin{bmatrix} 1 & x_2 & x_2^2 \end{bmatrix} + c_3 \cdot \begin{bmatrix} 1 & x_4 & x_4^2 \end{bmatrix}\Bigg) \cdot \begin{bmatrix} s \\ r_1 \\ r_2 \\ \end{bmatrix} = \\ \\ &= c_1 \cdot \begin{bmatrix} 1 & x_1 & x_1^2 \end{bmatrix} \cdot \begin{bmatrix} s \\ r_1 \\ r_2 \\ \end{bmatrix} + c_2 \cdot \begin{bmatrix} 1 & x_2 & x_2^2 \end{bmatrix} \cdot \begin{bmatrix} s \\ r_1 \\ r_2 \\ \end{bmatrix} + c_3 \cdot \begin{bmatrix} 1 & x_4 & x_4^2 \end{bmatrix} \cdot \begin{bmatrix} s \\ r_1 \\ r_2 \\ \end{bmatrix} = \\ \\ &= c_1 y_1 + c_2 y_2 + c_3 y_4 \\ &= \Lambda_1(0) y_1 + \Lambda_2(0) y_2 + \Lambda_4(0) y_4 \\ &= s \\ \end{split}\]
Thus, we have reconstructed the shamir secret sharing technique as a sort of a span problem, that is given a set of vectors \(v_1, v_2, v_3\) we have to find out if the span of those vectors contains a given point.
Observation: In this other formulation the three vectors do not have to be independent.
2 LSSS Scheme
So far we have shown that the shamir secret sharing scheme can be formalized in three different ways:
As a polynomial interpolation.
As a linear system.
As a span problem.
Let us now introduce a new scheme, called linear secret sharing scheme (LSSS), which is a secret sharing scheme in which the matrix \(A\), instead of being the specific matrix of the shamir scheme, is now an arbitrary matrix, that is we do not make any assumption about the invertibility of the matrix
\[\begin{bmatrix} a_{1,1} & a_{1, 2} & a_{1, 3} \\ a_{2,1} & a_{2, 2} & a_{2, 3} \\ a_{3,1} & a_{3, 2} & a_{3, 3} \\ a_{4,1} & a_{4, 2} & a_{4, 3} \\ \end{bmatrix} \cdot \begin{bmatrix} s \\ r_1 \\ r_2 \\ \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ \end{bmatrix}\]
There is a theorem by Amos Beimel, which demonstrates that linear secret sharing scheme is equivalent to a specific class of span programs.
2.1 Trivial Secret Sharing in LSSS
Consider a \((3, 3)\) secret sharing trivial scheme. Let us now formalize such scheme as a LSSS as follows
\[\begin{bmatrix} 1 & -1 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} s \\ r_1 \\ r_2 \\ \end{bmatrix} = \begin{bmatrix} s - r_1 - r_2 \\ r_1 \\ r_2 \end{bmatrix}\]
The span program in this case consists in finding the three coefficients \(c_1, c_2\) and \(c_3\) such that the following holds
\[ c_1 \cdot \begin{bmatrix} 1 & -1 & -1 \end{bmatrix} + c_2 \cdot \begin{bmatrix} 0 & 1 & 0 \end{bmatrix} + c_3 \cdot \begin{bmatrix} 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0\end{bmatrix}\]
Notice that in this case the solution is \(c_1 = c_2 = c_3 = 1\), since
\[ 1 \cdot \begin{bmatrix} 1 & -1 & -1 \end{bmatrix} + 1 \cdot \begin{bmatrix} 0 & 1 & 0 \end{bmatrix} + 1 \cdot \begin{bmatrix} 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0\end{bmatrix}\]
In this case the share reconstruction then is done as follows
\[c_1 (s - r_1 - r_2) + c_2 r_2 + c_3 r_2 = (s - r_1 - r_2) + r_1 + r_2 = s\]
2.2 Any LSS is Homomorphic
Suppose that you have two random vectors \(x_a\) and \(x_b\) that hide two secret values, \(s_a\) and \(s_b\)
\[\begin{split} x_a = \begin{pmatrix} s_a & r_{1, a} & r_{2, a} & \cdots \end{pmatrix} \\ x_a = \begin{pmatrix} s_b & r_{1, b} & r_{2, b} & \cdots \end{pmatrix} \\ \end{split}\]
and suppose you compute the shares of both secret using a matrix, that is
\[\begin{split} A \cdot x_a = y_a = \begin{pmatrix} \text{share}_{1, a} & \text{share}_{2, a} & \cdots \end{pmatrix} \\ \\ A \cdot x_b = y_b = \begin{pmatrix} \text{share}_{1, b} & \text{share}_{2, b} & \cdots \end{pmatrix} \\ \end{split}\]
then the share of the sum of the secrets is the sum of the shares of the individual secrets
\[\begin{split} y_a + y_b &= Ax_a + Ax_b \\ &= A(x_a + x_b) \\ &= A \begin{pmatrix} s_a + s_b & \text{rand} & \text{rand} & \cdots \end{pmatrix} \\ \end{split}\]
2.3 Span Programs in \(\mathbb{Z}_2\)
Notice that these secret sharing schemes can be implemented in arbitrary modular arithmetic. Let us now see an example of a secret sharing scheme the a binary field GF(2) (Galois Field 2) (also known as \(\mathbb{Z}_2\)), which is made up of two elements \(\{0, 1\}\) and that only the xor operation \(\mathbin{\oplus}\) that combines the elements as follows
\[\begin{split} 0 \mathbin{\oplus} 0 = 0 \\ 0 \mathbin{\oplus} 1 = 1 \\ 1 \mathbin{\oplus} 0 = 1 \\ 1 \mathbin{\oplus} 1 = 0 \\ \end{split}\]
Consider then that we have \(5\) parties, and that one of them, \(P_2\), comes with two vectors.
\[\begin{array}{c | c | c | c | c} \hline P_2 & 1 & 0 & 1 & 1 \\ \hline P_2 & 0 & 1 & 1 & 0 \\ \hline P_1 & 0 & 1 & 1 & 0 \\ \hline P_3 & 1 & 1 & 0 & 0 \\ \hline P_4 & 0 & 0 & 1 & 1 \\ \hline \end{array}\]
The span problem says: given some of the rows of the table above, can I find some combination of these rows so that I can obtain the vector \(\langle 1, 0, 0, 0 \rangle\). Depending on the rows we choose we can get different answers:
Assume for example that \(P_2\) and \(P_4\) get together. Can they obtain the secret? This can be expressed in terms of the following span problem: find \(c_1, c_2\) and \(c3\) such that
\[c_1 \cdot \begin{bmatrix} 1 & 1 & 0 & 1 \end{bmatrix} + c_2 \cdot \begin{bmatrix} 0 & 1 & 1 & 0 \end{bmatrix} + c_3 \cdot \begin{bmatrix} 0 & 0 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0\end{bmatrix}\]
in this case if \(c_1 = c_2 = c_3 = 1\) then we solved our problem.
If instead \(P_2\) meets up with \(P_1\), then we don't find any linear combination of those three rows that lets you obtain the result wanted.
2.3.1 How to get Secret Sharing
To actually get secret sharing from the setup we mentioned we simply need to multiply the matrix containing the rows for the various parties with a random vector containing the secret \(s\) and other random values \(r_i\).
\[\begin{bmatrix} 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} s \\ r_1 \\ r_2 \\ r_3 \\ r_4 \\ \end{bmatrix} = \begin{bmatrix} s + r_2 + r_4 \\ r_2 + r_3 \\ r_2 + r_3 \\ s + r_2 \\ r_3 + r_4 \\ \end{bmatrix}\]
Notice that since \(P_2\) has the first two rows of the matrix, he will receive two shares: \(s + r_2 + r_4\) and \(r_2 + r_3\).
Example: If \(s = 1\) and \(r_2 = r_3 = 0\), \(r_4 = 1\), then the shares for each party are computed as follows
\[\begin{array}{| c | c |} \hline P_2 & 0 \\ \hline P_2 & 0 \\ \hline P_1 & 0 \\ \hline P_3 & 1 \\ \hline P_4 & 1 \\ \hline \end{array}\]
2.3.2 Exam Question
The following question was taken from last year exam.
Question: Consider a secret sharing scheme involving \(3\) parties which uses the following access control matrix working in modulus \(100\)
\[\begin{array}{c | c | c | c} \hline A & 1 & 1 & 0 \\ \hline B & 0 & 1 & 1 \\ \hline C & 0 & 0 & -1 \\ \hline \end{array}\]
assume also that the following shares are revealed
\[\begin{split} A \longrightarrow 51 \\ B \longrightarrow 63 \\ C \longrightarrow 11 \\ \end{split}\]
What is the secret?
Answer: To find out the secret we need to multiply the shares by the coefficients that give us the vector \(\langle 1, 0, 0 \rangle\) by combining the rows of the matrix. Since
\[A - B - C = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}\]
we get that
\[s = 51 - 63 - 11 = -23 = 77 \mod 100\]
3 Access Structure
A LSSS can implement any monotone access structure. Consider that we have some participants, like \(P = \{P_1, P_2, P_3, P_4\}\), and assume we define a predicate, a policy, which defines a monotone access structure \(A \subseteq 2^P\). In our case,
\[A = \{\{P_1, P_2\}, \,\, \{P_1, P_3, P_4\}\}\]
Note that for an access structure like this to be "monotone" it means that we cannot use the NOT operation, and so that we are only "additive".
It can be proved that any such structure can be implemented as a LSSS. That is, we can support with an LSSS any boolean predicate such as
\[P_1 \land (P_2 \lor (P_3 \land P_4))\]
The problem is that this scheme may not be ideal, i.e. it may entail more than \(1\) share per partner.
Observation: The "problem" of the Shamir secret sharing scheme is that its based on "count", that is we only require that \(t\) or more participants get together, but participants are considered all equal. However in the real access control world policies are usually much more complex and subtle than this.
3.1 LSSS Matrix from AC Predicate
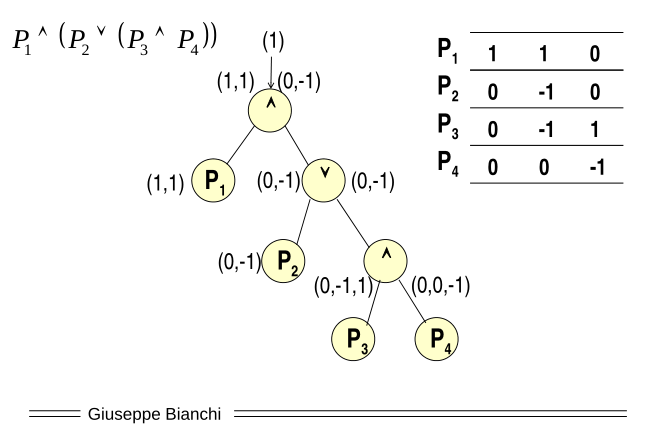
Let us now see how we construct an LSSS scheme starting from an Access Control (AC) predicate. For example assume we have the following predicate
\[P_1 \land (P_2 \lor (P_3 \land P_4))\]
we will start by constructing the tree of such predicate
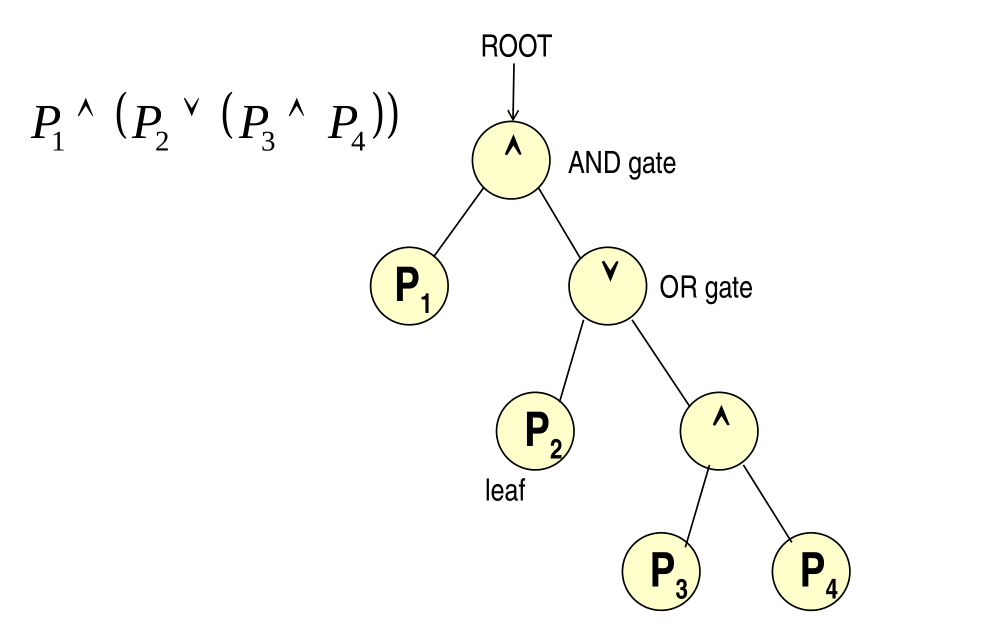
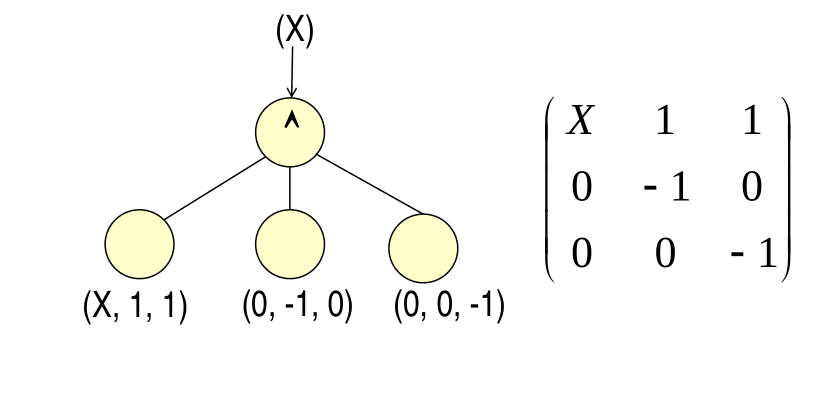
3.1.1 AND Gate
3.1.2 OR Gate
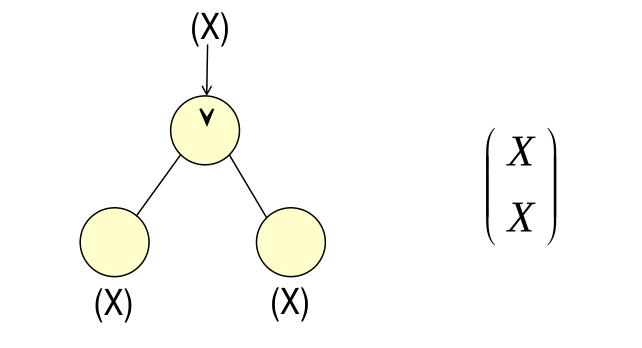
3.1.3 Matrix Construction