CNS - 42 - Elliptic Curve Crypto I
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: (50-ecc-basics.pdf)
Introduction: In this lecture we start with a minimal introduction to the world of elliptic curve cryptography.
1 Why Bother with ECC?
ECC stands for Elliptic Curve Cryptography. If you ask someone "why do we even use ECC?" he might answer that in ECC keys are shorter, and therefore it is more efficient to use such crypto. While this answer is not wrong, it is incomplete.
Remember that we often measure the security of an asymmetric crypto in terms of a what a symmetric crypto system would provide. When using RSA, to double the number of bits in the symmetric equivalent, you'd need to multiply by a factor of 5. Thus, in standard modulus arithmetic, the problem is scalability.

The key point thus is not only the fact that ECC keys are usually shorter, but rather that ECC scale much better than RSA.
Let us now gain an approximate intuition about why this is the case. To this end we note that the DLOG problem can tackled in various ways
In the most easy way it takes linear time to solve it.
Then, for any group, there is the pollard-$algorithm, which takes order \(\text{exp}(O(\sqrt{n}))\).
Finally, for the specific group \(\mathbb{Z}_p^*\) there is an even more efficient algorithm (still exponential), that takes \(\text{exp}(O(n^{1/3}))\).
2 Elliptic Curves
Elliptic curves are not ellipses, they are special cubic curves. The general expression for ane lliptic curve (Weistress) is the following
\[y^2 = x^3 + ax + b\]
where \(a\) and \(b\) are choosen such that \(4a^2 + 27b^3 \neq 0\). This means that by changing these two parameters we change the type of curve we're working with. Every elliptic curve has its own parameters.
Some example:
\(y^2 = x^3 - 3x + 1\)
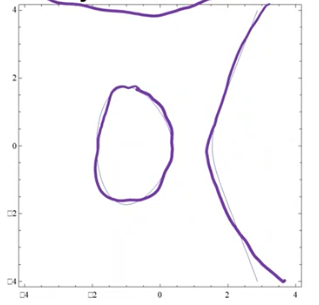
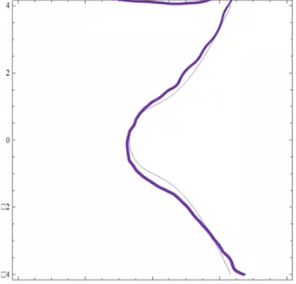
\(y^2 = x^3 + x + 1\)
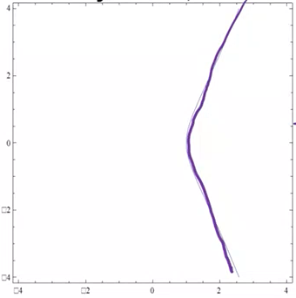
\(y^2 = x^3 - 1\)
2.1 Elliptic Points Addition
To do cryptography we need a group, which requires two things: a set of elements and an operation to be performed on those elements. Lets start with the latter one: the operation.
We will denote our new operation with the symbol \(+\), but its important to keep in mind that the way in which we'll use such symbol is nowhere close to the way it is typically used. The main idea of our operation is to define an operation that is applied to two points, \(P\) and \(Q\), and that gives back a third point \(R\) and such that it gives an algebraic group structure.
2.1.1 \(P + Q\)
The operation is defined by using the following graph:
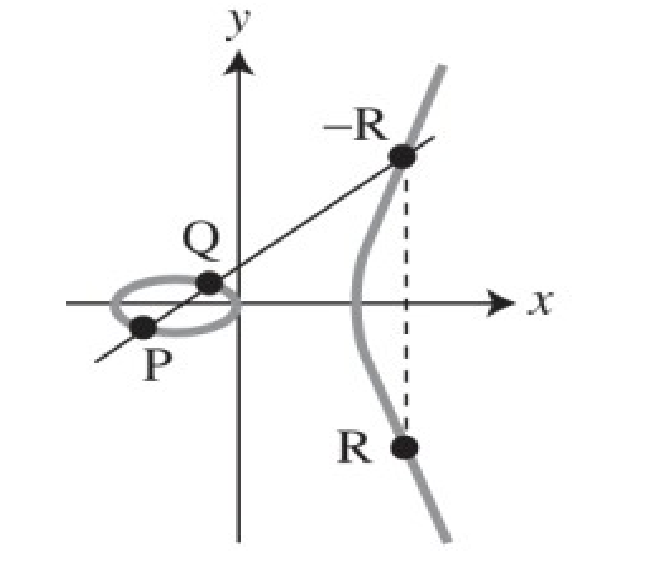
The operation can also described as follows: we take two points \(P\) and \(Q\), and let us cross the line between those two points. This line we just crossed will interesect the graph in another point (this happens expect in \(1\) case, which we will fix later). Let's now reflect the third interesection point of the line on the x-axis, and let us call \(R\) the resulting point.
2.1.2 \(P + P\)
If we instead want to sum the same point, then the operation is defined as follows
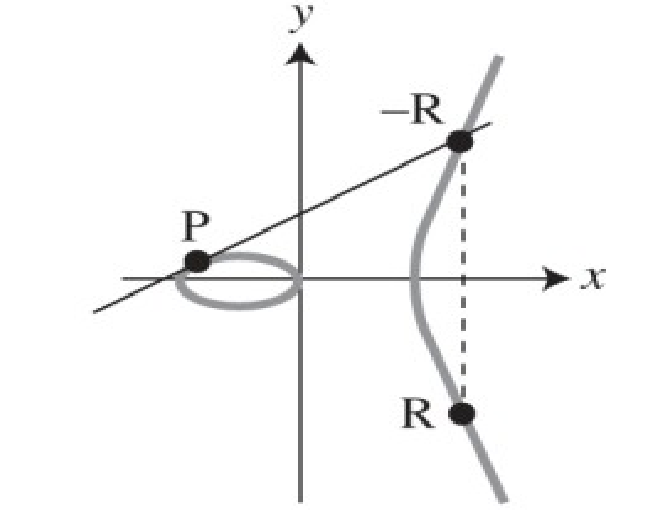
This time we take the tangent on point \(P\). Once again, this tanget will cross the graph in another point, which always exist apart from a single case, which we will fix later on.
2.1.3 \(P + O = P\)
To complete the the curve we add an extra point that we call \(0\) and that represents infinity. Notice that
\[P + O = P\]
graphically,

2.2 Algebraic Expressions
The geometric interpretation that we saw before give rise to the following formulas: consider
\[\begin{split} P &= (x_1, y_1) \\ Q &= (x_2, y_2) \\ R &= P + Q = (x_3, y_3) \\ \end{split}\]
Then the coordinate of the final points are computed as follows
\[\begin{split} x_3 = \lambda^2 -x_1 - x_2 \\ y_3 = \lambda(x_1 - x_3) - y_1 \end{split}\]
where the \(\lambda\) term is different depending on whether \(P = Q\) or \(P \neq Q\).
\[\lambda = \begin{cases} \displaystyle{\frac{y_2 - y_1}{x_2 - x_1}} & P \neq Q \\ \\ \displaystyle{\frac{3x_1^2 + a}{2 y_1}} & P = Q \\ \end{cases}\]
2.2.1 \(P \neq Q\) sketch
Given points \(P = (x_1, y_1)\) and \(Q = (x_2, y_2)\), assuming that \(P \neq Q\) then the line that passes through both of them has the following algebraic expression
\[y = y_1 + \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) = \lambda(x - x_1) + y_1\]
We now need to find the third point where the graph interesects this line. To do so we plug the \(y\) value we have found in our elliptic curve formula to get
\[(\lambda(x - x_1) + y_1)^2 = x^3 + ax + b\]
Notice however that we already know two solutions of such equation: \(x_1\) and \(x_2\). Therefore we know that
\[\begin{split} (\lambda(x - x_1) + y_1)^2 &= x^3 - \lambda^2 x^2 + \ldots \\ &= x^3 + ax + b \\ &= (x - x_1)(x - x_2)(x - x_3) \\ &= x^3 - (x_1 + x_2 + x_3)x^2 + \ldots \\ \end{split}\]
Thus, without any computation we get that
\[\lambda^2 = x_1 + x_2 + x_3 \longrightarrow x_3 = \lambda^2 -x_1 - x_2\]
2.2.2 \(P = Q\) sketch
In this other case we have that the equation of the tangent at point \(P\) is...
3 EC Over \(\mathbb{Z}_p\)
Instead of working with real numbers in \(\mathbb{R}^2\), we will now restrict ourselves to integer numbers and modulus prime. In this case we define a curve, that is a discrete set of points denoted as \(E_p(x, y)\) such that
\[\begin{cases} x, y \in \mathbb{Z}_p \\ y^2 \mod p = x^3 + ax + b \mod p \end{cases}\]
Notice that now, instead of having a curve with infinite points, we have a finite field, that is a curve with a finite number of points.
3.1 Example 1
Consider for example the elliptic curve \(y^2 = x^3 + x + 1\) defined over \(\mathbb{Z}_5\). To generate such set we have to generate all points \((x, y)\) with \(y = 0, \ldots, 4\), \(x = 0, \ldots, 4\) and check if they satisfy the equation. If they do, they are added to the set \((x, y) \in E(\mathbb{Z}_5)\). The final result is
\[E(Z_5) = \{O, (0, 1), (0, 4), (2, 1), (2, 4), (3, 1), (3, 4), (4, 2), (4, 3)\}\]
Notice that the number of points of the curve changes depending on the parameters of the curve. Typically the number of points is even.
Notice also that in this case the point \(P = (0, 1)\) is a generator, because by applying iteratively the "sum" we defined before we can get all the other points.
3.2 Example 2
Consider plotting the points of the curve \(y^2 = x^3 + x\) over \(\mathbb{F}_{23}\).
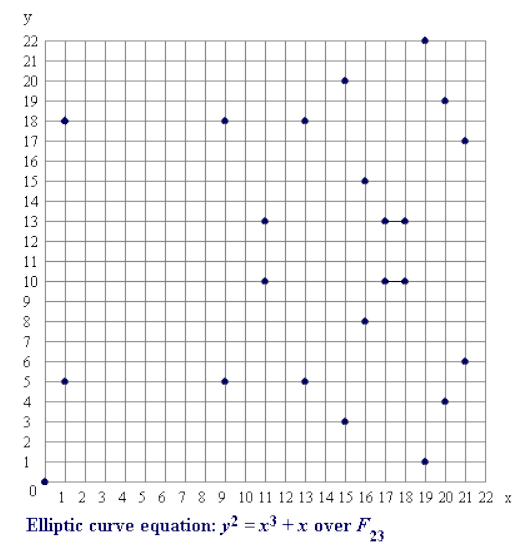
Notice that the plot above is very scattered and irregular. This is exactly why we like Elliptic Curves in crypto: because when we restrict the elliptic curve to finite fields, we get an irregular plot.
3.3 EC Group
It can be proved that \((E(\mathbb{Z}_p), +)\) is an (abelian) group because:
Addition is closed on set \(E\) (by definition).
Addition is commutative.
\(O\) is an identity wrt to addition.
Every point \(P\) in \(E\) has an inverse \(-P\) wrt to addition.
Associative property holds. (harder to prove in generality)
3.3.1 Useful Properties
If we want to use such groups in cryptography we need to find an hard operation that is easy on the other side. Now, given \(P\) and \(k\), it is easy to compute \([k]P\), that is it is easy to compute
\[\underbrace{P + P + \ldots + P}_{k \text{ times }}\]
But, given \(P\) and \([k]P\), it is "generally" hard to compute \(k\).
By "generally" we means that the hardness of the problem depends on the choosen curve. There are standards that recommend certain curves instead of others.