CNS - 43 - Elliptic Curve Crypto II
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: (50-ecc-basics.pdf)
Introduction: In this lecture we will see how elliptic curves can be used to create two specifics cryptography constructions: the diffie-hellman key exchange (ECDH) and the diginal signature (ECDSA).
1 EC Crypto
Ellipic Curve crypto was inveted indipendently in 1985 by two guys, Neal Koblitz and Victor Miller, who both understood how elliptic curve, previoulsy only an algebraic object of study, could be applied to cryptography.
The usage for cryptogaphy is based on the elliptic curve discrete log problem (ECDLP), which can be stated as follows: Given a point \(P\) and another point \([k]P\) obtained by summing \(P\) with itself \(k\) times, and I challenge you to compute such integer \(k\).
We will now enter into the details of the following algorithms, which have been approved by NIST in 2005 and which are considered suite B ciphers from the NSA.
ECDH (Elliptic Curve Diffie Hellman)
ECDSA (Elliptic Curve Digital Signature Algorithm)
2 ECDH
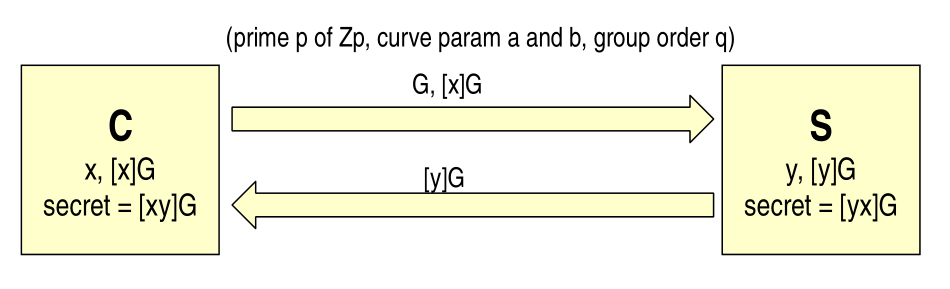
ECDH works exactly as DH, the only difference being is that instead of running the operations on \(\mathbb{Z}_p^*\), we run it over an EC group.
3 Diginal Signature
ECDSA is the ellipic curve version of a standard diginal signature called DSA, which was invented by Vanstone and proposed by INST in august 1991. Its a variant of ElGamal, which means its Dlog based.
Observation 1: Pure cryptographers do not like DSA, because there is no security proof about it. Unfortunately a better signature, which is called Schnorr signature, was patented.
Trivia: ECDSA was broken in the Playstation network in 2010 because of incorrect usage.
3.1 DSA
Let's start with the standard digital signature algorithm constituents:
A multiplicative group \(\mathbb{Z}_p^*\), with \(p > 2\) usually a strong prime, that is \(p = 2q + 1\) with \(q\) large prime.
A generator \(g\) such that \(g^x \mod p\) spans all group elements.
A private/public key pair \(d, y = g^d \mod p\).
3.1.1 Signing
When we want to sign a message \(m\) the following steps have to be taken:
We first generate a random \(k\) in the \((1, q)\), which is the first half of the group.
We then compute \(r = (g^k \mod p)\), but since this value might be greater than \(q\) we also chop it using \(\mod q\). At the end thus we have the following value
\[r = (g^k \mod p) \mod q\]
We also compute the following
\[s = k^{-1} \cdot (H(m) + d \cdot r) \mod q\]
The final signature is \((r, s)\).
3.1.2 Verifying
When instead we want to verify the signature \((r, s)\) of a given message \(m\) we do the following:
We first invert \(s\) and compute
\[u_1 = s^{-1}H(m) \mod q = \frac{k}{H(m) + dr} \cdot H(m) \mod q = \frac{k H(m)}{H(m) + dr} \mod q\]
Then we compute
\[u_2 = s^{-1}r \mod q = \frac{k}{H(m) + dr} \cdot r \mod q = \frac{kr}{H(m) + dr} \mod q\]
Finally, we verify that
\[((g^{u_1} \cdot y^{u_2} \mod p) \mod q) = r\]
This check makes sense since
\[\begin{split} ((g^{u_1} \cdot y^{u_2} \mod p) \mod q) &= \bigg(g^{\frac{k H(m)}{H(m) + dr}} \cdot (g^{d})^{\frac{kr}{H(m) + dr}} \mod p \bigg) \mod q \\ &= \Bigg(g^{\frac{k H(m)}{H(m) + dr} + \frac{krd}{H(m) + dr}} \mod p\Bigg) \mod q \\ &= \Bigg(g^{\frac{k(H(m) + dr)}{H(m) + dr}} \mod p\Bigg) \mod q \\ &= \Bigg(g^{k} \mod p\Bigg) \mod q \\ &= r \\ \end{split}\]
3.2 ECDSA
In ECDSA initially we setup the various parameters:
The curve \(E(\mathbb{Z}_p)\)
The order of the curve \(n\), which is a prime number. Note that \(n\) can either be greater or lower than \(p\).
A point \(P\), which generates the curve.
A value \(d\), which is our private key \(\mod n\).
A point \(Q = [d]P\), which is our public key.
3.2.1 Signing
When we want to sign a message \(m\) using ECDSA the following steps have to be taken:
We generate a random integer \(K \in (1, \ldots, n-1)\).
We compute the point \(kP = (x_1, y_1)\) using our elliptic curve group we have previously defined.
We compute \(r = x_1 \mod n\)
We compute \(k^{-1} \mod n\)
We compute \(s = k^{-1} \cdot(H(m) + dr)\)
The final signature is then given by \((r, s)\).
Note that the only operation regarding elliptic curves is when we compute the point \(kP\). Since this operation can be computationally expensive, it might get optimized. Doing so however might break the signature.
Also note that the integer \(k\) must be unique per signature and unpredictable. If these requirements are not met, then the signature might be broken.
3.2.2 Verfying
When instead we want to verify the signature \((r, s)\) of a given message \(m\) we do the following:
From the message \(m\) we compute the hash \(H(m)\).
From \(s\) we compute
\[w = s^{-1} \mod n = \frac{k}{H(m) + dr} \mod n\]
We then compute \(u_1\), \(u_2\) as follows
\[\begin{split} u_1 &= H(m) w &\mod n &= \frac{H(m) k}{H(m) + dr} \mod n \\ u_2 &= r w &\mod n &= \frac{r k}{H(m) + dr} \mod n \\ \end{split}\]
Then we compute the elliptic point
\[\begin{split} u_1 P + u_2 Q &= u_1 P + u_2 (d P) \\ &= \frac{H(m) k}{H(m) + dr} P + \frac{r k d}{H(m) + dr} P \\ &= \frac{k(H(m) + rd)}{H(m) + dr} P \\ &= (x_0, y_0) \\ \end{split}\]
Finally, we check that given \(v = x_0 \mod n\) we have that
\[v = r\]
3.2.3 What if \(k\) is predicted?
Notice that if \(k\) is predicted, then the knowledge of the longterm private key would be disclosed. Indeed, consider a signature \((r, s)\) and assume we know \(k\), then we know that
\[s = k^{-1}(H(m) + rd) \mod n\]
but notice that this gives us an equation in which the only unknown is \(d\). By solving for \(d\) we get
\[d = (sk - H(m))r^{-1} \mod n\]
and thus \(d\) is easily computed.
3.2.4 What if \(k\) is repeated?
Assume now that \(k\) is repeated. That is, assume we have two signatures \((r, s_1)\) and \((r, s_2)\). Notice that the \(r\) value is the same in both signature because we assume that the underlying \(k\) vale is also teh same. But then we have that
\[\begin{cases} s_1 = k^{-1}(H(m_1) + rd) \mod n \\ s_2 = k^{-1}(H(m_2) + rd) \mod n \\ \end{cases} \implies \begin{cases} k = s_1^{-1} (H(m_1) + rd) \mod n \\ k = s_2^{-1} (H(m_1) + rd) \mod n \\ \end{cases}\]
which means that we have two equations in two unknowns \(k\) and \(d\). We can solve it to find
\[d = (s_1 H(m_2) - s_2 H(m_1))r^{-1}(s_2 - s_1)^{-1} \mod n\]
to once again compute \(d\).
Observation: This type of attacked happend for real in \(2010\), and the target was Sony's Playsation 3 signature.