IR - 01 - Inverted-Index I
Data:
Sito corso: link
In questa prima lezione abbiamo introdotto la principale struttura dati utilizzata per risolvere i problemi di indicizzazione, l'indice inverso (inverted-index).
L'information retrieval (IR) studia una serie di tecniche e metodologie che permettono ad un utente di cercare delle informazioni all'interno di una collezione di dati non strutturata, in modo da soddisfare l'information need dell'utente. Tipicamente per "dati non strutturati" si intende documenti testuali.
Le tecniche sviluppate e studiare dal campo dell'IR sono utilizzate in molti contesti diversi. Tra questi troviamo anche i motori di ricerca come Google. Tali motori ci permettono di trovare, tra tutte le pagine presenti nel web, quelle che sono più "adeguate" rispetto alla nostra query. Detto oquesto, le problematiche di retrieval non sono solamente presenti in un contesto di web search. Altri contesti in cui è necessario poter effettuare delle ricerche su vaste collezioni di documenti sono:
E-mail search.
Computer filesystem search.
Legal information retrieval.
Prima di iniziare è importante menzionare che nella prima parte del corso assumeremo sempre di lavorare con collezioni di documenti statiche, ovvero di collezioni che non cambiano nel tempo.
Il modello classico di ricerca che dobbiamo sempre tenere in mente mentre definiamo la struttura dei nostri indici di retrieval è descritto dal seguente diagramma
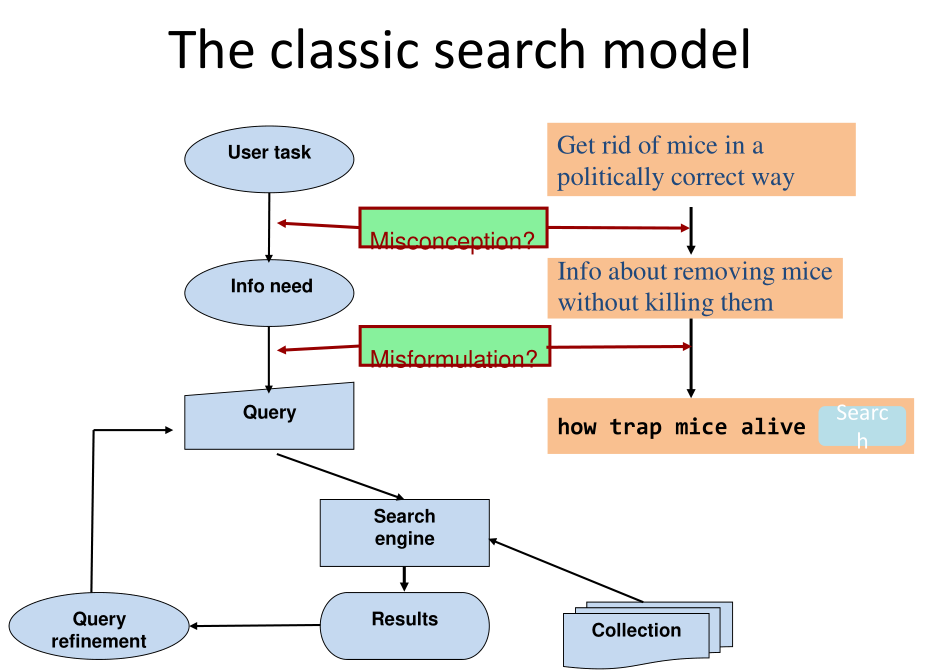
L'utente, che vuole risolvere un determinato problema (user task), necessita di un qualche tipo di informazione (information need). Al fine di ottenere questa informazione effettua delle richieste (queries), ad un sistema di retrieval, come ad esempio una search engine online. La search engine utilizza delle strutture dati interne, costruite a partire da una collezione documentale (collection) per ottenere una serie di risultati iniziali (results). Se l'utente non è soddisfatto dei risultati ottenuti può provare a modificare la sua query (query refinement), al fine di esplicitare in modo più chiaro cosa sta cercando.
Osservazione: quando scriviamo una query su google, il link fornito da google non punta direttamente al sito su cui vogliamo andare, ma punta ad un server di google, che a sua volta fa un re-indirizzamento al sito richiesto. Questa operazione viene fatta da google per ottenere del feedback dall'utente ed essere in grado di capire qual è stato il particolare link scelto dall'utente tra tutti quelli riportati dalla search engine. Questo dato può poi essere utilizzato per cercare di migliorare i documenti scelti nelle successive query.
Dato che molto spesso è difficile stabilire quale sia effettivamente l'informazion need dell'utente, in quanto molto spesso questa informazione è ignota perfino all'utente stesso, abbiamo bisogno di metodi più chiari e concreti per stimare quanto buoni siano i risultati trovati da un sistema di IR.
A tale fine vengono definite due misure, che ritroveremo più avanti e che sono:
Precision: definita come la frazione dei documenti ritornati che sono rilevanti per lo specifico information need dell'utente rispetto al numero totale di documenti ritornati.
\[ \text{Precision } = \frac{\text{# relevant returned docs}}{ \text{# total returned docs}} \]
Recall: definita come la frazione dei documenti rilevanti ritornati rispetto al numero totale di documenti rilevanti presenti nella collezione.
\[ \text{Recall } = \frac{\text{# relevant returned docs}}{\text{# total relevant docs in collection}} \]
Notiamo che queste due misure presentano tra loro il seguente trade-off:
Più preciso un sistema di IR è, e meno recall avrà, in quanto, al fine di ritornare solamente i documenti utili, limiterà inevitabilmente il numero di documenti ritornati.
Viceversa, più un sistema di IR avrà una recall alta, e meno sarà preciso, in quanto pur di prendere tutti i documenti utili ritornerà necessariamente alcuni documenti non utili, ovvero alcuni falsi-positivi.
Per cercare di capire quali documenti ritornare e quali documenti non ritornare, è possibile utilizzare una funzione di ranking, che permette di ordinare i documenti ritornati in base alla loro rilevanza per l'utente. Queste funzioni saranno discusse in una futura lezione.
Andiamo adesso a vedere un primo modello di retrieval che ci permette di rispondere ad alcune semplici query.
Vogliamo fornire un sistema che sia in grado di ritornare i documenti in cui appaiono determinate solo parole e non altre. In particolare vogliamo essere in grado di soddisfare query del tipo
\[ \text{Brutus AND Caesar but NOT Calpurnia} \]
Senza utilizzare dei meccanismi di IR, potremmo risolvere questo problema con i seguenti metodi:
SQL query: così facendo però mi devo scorrere tutti i documenti presenti nella mia base dati in modo iterativo più volte, andando quindi a pagare un costo lineare.
Grep, tool di unix/linux ottimizzato per trovare delle stringhe in un documento. Anche se ottimizzato, ci mette comunque un tempo lineare, ed inoltre non ci permette di matchare query più generale della forma
\[ \text{"Generale \k Cesare"}\]
dove con \(\text{\k}\) si intende la presenza di \(k\) parole qualsiasi tra la parola \(\text{Generale}\) e la parola \(\text{Cesare}\). Infine, grep non ha criteri per ordinari i risultati.
Andiamo quindi a vedere una prima soluzione offerta dal campo del retrieval.
L'idea fondamentale per cercare di rispondere a query del genere è l'utilizzo di una struttura dati di tipo bitmap, che viene utilizzata per memorizzare le occorrenze dei termini nei vari documenti. Possiamo visualizzare la bitmap di interesse nel seguente modo
Notiamo come le righe della bitmap rappresentano parole (o termini) diversi, mentre le colonne della bitmap rappresentano documenti diversi. Se indichiamo con \(B[i, j]\) il contenuto della bitmap nelal cella \([i, j]\) troviamo che
\[B[i, j] = \begin{cases} 1 \,&,\,\, \text{il termine } i \text{-esimo è presente nel } j \text{-esimo documento} \\ 0 \,&,\,\, \text{il termine } i \text{-esimo non è presente nel } j \text{-esimo documento} \\ \end{cases}\]
Questa struttura dati prende il nome di matrice di incidenza dei termini nei documenti, e ci permette di stabilire, per ogni termine \(t\), i documenti \(d\) in cui compare il termine \(t\).
Una volta che abbiamo questa struttura dati, per rispondere a query come quella riportata in precedenza possiamo sostituire ogni termine della query con il rispettivo vettore riga presente nella bitmap e combinare i vari vettori tra loro tramite delle operazioni logiche bit-a-bit di \(\text{AND, OR o NOT}\), come riportato dal seguente esempio
\[\begin{split} \text{Caesar} &\longrightarrow \text{11011} \\ \text{Brutus} &\longrightarrow \text{11010} \\ \text{Calpurnia} &\longrightarrow \text{01000} \\ \text{Brutus AND Caesar} &\longrightarrow \text{11010} \land \text{11011} = \text{11010} \\ \text{NOT Calpurnia} &\longrightarrow \neg \text{01000} = \text{10111} \\ \text{Brutus AND Caesar BUT NOT Calpurnia} &\longrightarrow \text{11010} \land \text{11011} \land \neg \text{01000}= \text{10010} \\ \end{split}\]
NOTA BENE: Questo tipo di rappresentazione è detta rappresentazione densa in quanto vengono memorizzate sia le entrate nulle e sia quelle non nulle. È facile vedere che questo tipo di rappresentazione non è molto efficiente in termine di risorse utilizzate. Supponiamo infatti di avere la seguente situazione
\[\begin{cases} \text{totale documenti} &= 1000000 \,\, \text{(1 milione)} \\ \text{token per documento} &= 1000 \\ \text{bytes per token in media} &= 6 \\ \text{numero di termini distinti} &= 500000 \\ \end{cases}\]
segue quindi che la nostra collezione peserà intorno ai
\[\begin{split} \text{size collection} &= \text{totale documenti } \times \text{token per documento} \times \text{bytes per token in media} \\ &= 1000000 \times 1000 \times 6 \\ &= 6 \times 10^{9} \\ &= 6 \text{GB} \\ \end{split}\]
mentre la matrice di incidenza avrà un numero di \(0\) e \(1\) pari a
\[\begin{split} \text{size matrice} &= \text{totale termini distinti} \times \text{totale documenti} \\ &= 500000 \times 1000000 \\ &= 500000000000 \\ &= 5 \times 10^{11} \\ \end{split}\]
e sarà composta principalmente da \(0\), con non più di \(1\) miliardo di bit \(1\), in quanto tendenzialmente un testo contiene un numero di parole distinte limitate. Utilizzare questo tipo di struttura dati porta dunque ad un estremo spreco di risorse.
Dato che non possiamo utilizzare la bitmap interamente per le ragioni riportate precedentemente, l'idea è quella di convertire la bitmap utilizzando una rappresentazione sparsa, in cui vengono memorizzate solamente le entrate della bitmap con il bit a \(1\). La struttura dati risultante prende il nome di inverted index, e contiene, per ogni termine \(t\), una lista che identifica tutti e soli i documenti \(d\) che contengono il termine \(t\). All'interno dell'indice i documenti sono identificati da dei numeri seriali, chiamati \(\text{docIDs}\).
L'invertex index è quindi strutturato come segue: abbiamo un dizionario che contiene una lista di termini, e per ogni termine \(t\) nel nostro dizionario abbiamo un puntatore che punta alla lista dei \(\text{docIDs}\) relativi a documenti in cui è presente quel termine. Queste liste sono anche chiamate posting lists.
\[\begin{split} \text{Brutus} &\longrightarrow [1, 2, 4, 11, 31, 45] \\ \text{Caesar} &\longrightarrow [1, 2, 4, 5, 6, 16] \\ \text{Calpurnia} &\longrightarrow [2, 31, 54, 101] \\ \end{split}\]
Le posting lists associate ad ogni termine del dizionario sono liste di dimensioni variabile in quanto, anche sotto ipotesi di collezione statica, queste liste crescono durante la fase di indicizzazione. Infine, i \(\text{docIDs}\) contenuti in queste liste vengono poi ordinati tra loro per favorire determinate operazioni successive.
Andiamo adesso a vedere come è possibile costruire e utilizzare questa struttura dati.
Prima di poter iniziare la vera e propria costruzione dell'inverted index, ci sono varie fasi di elaborazione e processamento che i documenti devono subire. Queste fasi vengono effettuate per trasformare la sequenza di simboli che appare in un documento in una sequenza di elementi atomici che possono poi essere inseriti all'interno dell'indice. Tra questi steps troviamo anche i seguenti
Estrazione dei dati testuali dal documento: Potenzialmente molto complicato, specialmente se vogliamo parsare file come pdfs memorizzati come immagini. In questa fase potrebbe anche essere presente un modulo che capisce la particolare lingua che si sta estraendo, nel caso in cui si stanno analizzando collezioni contenenti documenti scritti in lingue diverse.
Tokenizzazione: Spazi e punteggiatura possono essere utilizzati per dividere il testo in elementi linguistici distinti, anche se bisogna stare attenti, in quanto questo tipo di processamento può perdere delle informazioni.
Utilizzo di modelli linguistici: Nell'inglese si usa lo stemming, che consiste nel matchare varie parole rispetto alla propria radice. Lo stemming separa la radice dalla desinenza, e memorizza solo la radice. Per le lingue morfologicamente ricche come l'italiano lo stemming non riesce a dare dei grandi risultati. Si applica quindi un altro processamento, chiamato lemmatizzazione, che consiste nel riportare ogni parola alla sua "forma base". Per i verbi la forma base è la forma all'infinito. In questo step si può anche scegliere di eliminare alcune parole molto comuni, chiamate stop words. Ad esempio nella lingua inglese parole come \(\text{the}\), \(\text{a}\), \(\text{to}\), \(\text{of}\), possono essere eventualmente tolte. Questa scelta non viene fatta per migliorare la qualità del modello, ma solo per risparmiare lo spazio utilizzato, in quanto le posting lists associate alle stop-words tendenzialmente saranno molto grandi. Infine ci può essere anche un processo di normalizzazione, in cui termini simili tra loro vengono matchati ad una stessa forma. Ad esempio "U.S.A." viene matchata con USA.
Indexer: Ultimo step nel processo, in cui i token generati dalla tokenizzazione e modificati dal passo precedente vengono utilizzati per costruire l'indice inverso finale.
In generale la fase di pre-processamento è un aspetto molto critico e problematico, e bisogna quindi porre molta attenzione a come vengono pre-processati i documenti. Ad esempio, se si sceglie di applicazione lo stemming per la costruzione dell'indice, lo si dovrà anche applicare successivamente, durante il processamento delle query.
La costruzione dell'inverted index viene effettuata in vari steps, riporati a seguire
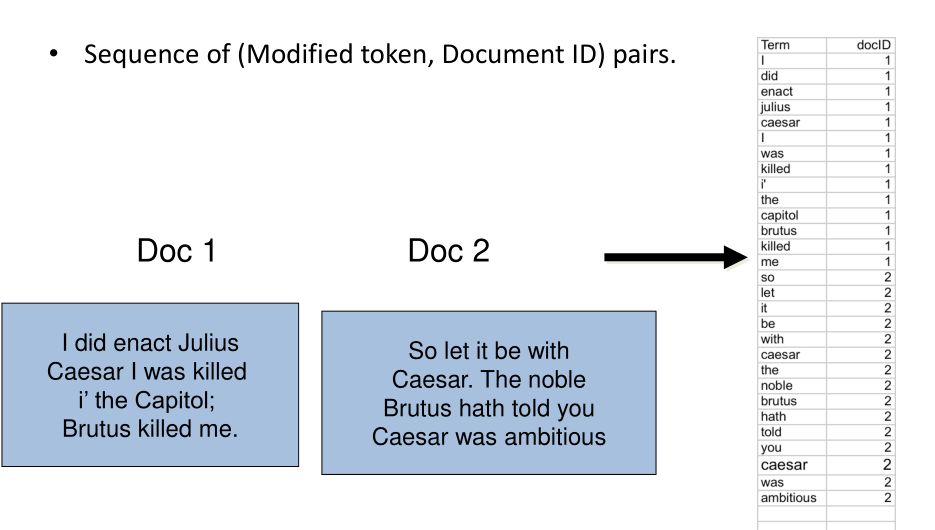
Token sequence: Come prima cosa ci si costruisce una sequenza di coppie \(\text{(modified token, docID)}\), che esprimono il fatto che quel modified token si trova nel documento associato a docID. Per collezioni veramente grandi potrebbe essere impossibile far entrare questa sequenza direttamente in memoria. Esistono quindi dei metodi che permettono di dividere questa operazione in vari blocchi, oppure di splittare questa operazione su più macchine diverse.
Sort: La sequenza di coppie viene ordinata, prima rispetto al termine e poi rispetto al docID.

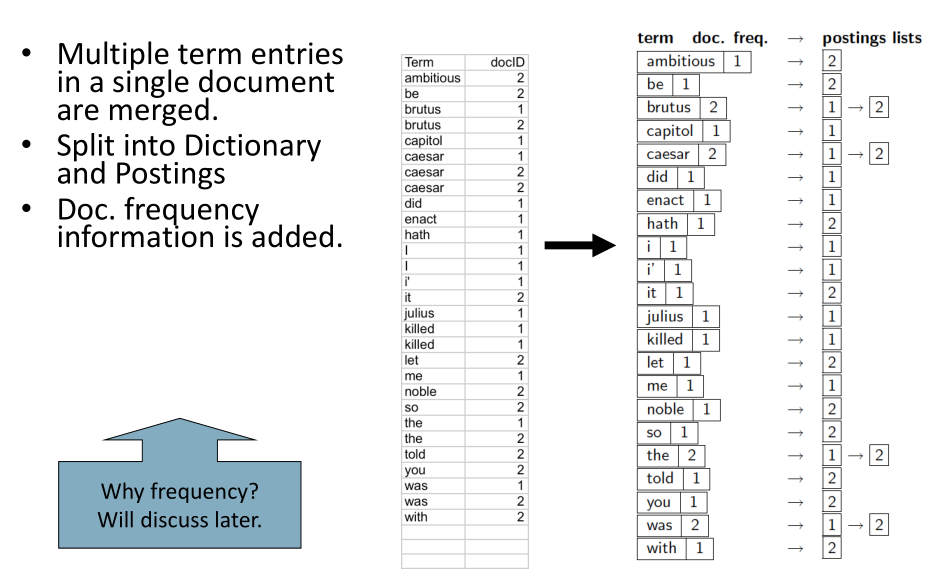
Dictionary and Postings: Le entry multiple con la stessa coppia \(\text{(term, docID)}\) vengono unite assieme, andando eventualmente ad inserire informazioni sulla frequenza del termine all'interno del documento. Informazioni di questo tipo vengono utilizzate nelle trattazione delle funzioni di ranking, che vedremo successivamente nel corso.
Continuando, si procede scansionando la sequenza di coppie e costruendo le postings lists per ogni termine. Una volta che ho terminato tutte le coppie con un particolare termine, aggiungo l'informazione sulla docFrequency del termine, che rappresenta il numero di documenti in quel quel termine appare, e mi muovo sul prossimo termine.
Una volta che abbiamo costruito l'indice,per processare una query con un AND, come
\[\text{Brutus AND Caesar}\]
possiamo procedere come segue:
Prendere la posting list associata a Brutus;
Prendere la posting list associata a Caesar;
Fare il merge delle due posting lists.
Un esempio di pseudo-codice scritto in python in grado di rispondere a delle query della forma \(\text{term1 AND term2}\) è il seguente
def intersect(term1, term2): answer = [] # return posting lists associated with each terms p1 = InvIndex(term1) p2 = InvIndex(term2) while p1 is not None and p1 is not None: if p1.docID == p2.docID: answer.append(p1.docID) p1 = p1.nextDoc p2 = p2.nextDoc elif p1.docID < p2.docID: p1 = p1.nextDoc else: p2 = p2.nextDoc return answer
Notiamo che dato che le posting lists sono entrambe ordinate, fare il loro merging richiede tempo \(O(x + y)\), dove \(x\) e \(y\) sono le lunghezze delle due posting lists.
Infine, il modo in cui viene processato un \(\text{OR}\) o un \(\text{NOT}\) è molto simile a quanto appena visto per l'\(\text{AND}\), in quanto si basa sempre su uno scansionamento lineare delle posting lists dei termini presenti nella query.
Osservazione 1: Come abbiamo appena visto, nella costruzione di un sistema IR ci sono sempre due fasi, che sono:
Costruzione dell'indice.
Data la query, sfrutto l'indice per arrivare al risultato.
Osservazione 2: La differenza tra rappresentazione densa e rappresentazione sparsa è fondamentale da tenere a mente durante il proseguimento del corso. Quando abbiamo una matrice che contiene molte entrate nulle, possiamo scegliere due modalità diverse per rappresentare la matrice:
Nella rappresentazione densa si memorizzano sia le entrate nulle che le entrate non nulle. Questo comporta un maggiore costo di memoria, ma potrebbe rendere l'esecuzione di alcune operazioni più efficienti.
Nella rappresentazione sparsa si memorizzano solamente le entrate non nulle. Questo mi permette di salvare delle risorse di memoria, ma potrebbe rallentare l'esecuzione di alcune operazioni.