IR - 03 - Distributed and Dynamic Indexing
Data:
Sito corso: link
In questa lezione abbiamo trattato due temi principali: inizialmente abbiamo visto delle teniche e dei metodi che ci permettono di costruire un indice distribuito tra più macchine, e poi abbiamo visto delle tecniche che ci permettono di gestire un indice con una collezione dinamica di documenti.
Fino al 2004 Google utilizzava approcci simili a quelli descritti nella precedente lezione per gestire la costruzione degli indici. In particolare l'indicizzazione veniva fatta su una macchina, o comunque in modo indipendente su più macchine. Ad un certo punto però è stato necessario effettuare una indicizzazione distribuita su più macchine. È nato quindi il famoso paradigma MapReduce, che si basa sull'utilizzo di una architettura distribuita master/slave per risolvere problemi che necessitano l'elaborazione di grandi quantità di dati.
Esempio: Consideriamo di avere una server farm di \(1000\) computers, in cui ogni nodo ha il \(99.9\%\) di uptime. Qual è l'uptime del sistema, ovvero qual è la percentuale di tempo in cui tutte le macchina sono accese? Tale probabilità è così calcolata
\[P(\text{tutte macchine accese}) = (0.999)^{1000} \approx 0.367\]
Notiamo che lavorare in modo distribuito con tanti server garantisce delle proprietà interessanti. Ad esempio la probabilità che tutti i nodi siano spenti o rotti è pari a
\[P(\text{tutte macchine spente}) = (0.0001)^{1000}\]
che è una probabilità estremamente bassa.
L'idea alla base della maggior parte delle tecniche per gestire un indice in modo distribuito è quella di classificare le macchine del nostro cluster in due classi: i masters, e gli slaves.
Le macchine master sono considerate safe da eventuali guasti, e dunque bisogna continuamente controllare che stiano lavorando in modo corretto. Il loro compito consiste nel coordinare il lavoro da svolger assegnando ai vari slaves particolari segmenti del lavoro globale. Tipicamente esistono delle macchine master di backup in caso quelle correnti smettino di funzionare. In generale però i masters occupano una frazione molto ridotta del cluster di macchine a nostra disposizione.
Gli slaves invece sono semplici macchine che eseguono gli ordini dei masters. Possono essere sostituiti e non è un problema se smettono di funzionare per un tempo limitato.
La divisione del lavoro effettuata dai masters deve avvenire sia a livello di macchina--ovvero più macchine devono lavorare contemporaneamente--e sia a livello di task--ovvero il compito da eseguire viene spezzato in parti atomiche da assegnare ai vari slaves.
Con questo punto di vista distribuito il processo di costruzione dell'indice non viene più visto come una singola, monolitica, attività che viene assegnata, con dati diversi, a diverse macchine, ma viene invece spezzato in vari sotto-tasks, che possono essere eseguiti in modo parallelo.
Nel caso della costruzione di un indice distribuito, abbiamo i seguenti due sotto-tasks paralleli:
Parsing: Il parsing è il processo che permette, partendo da un documento in input, di ottenere le coppie \((\text{term}, \text{docID})\). Le macchine slave che eseguono questo processo sono chiamate parsers. Un master node assegna ad un idle parser un dato documento, e i parsers scrivono le coppi \((\text{term}, \text{docID})\) che hanno trovato in \(j\) partizioni. Ogni partizione contiene un range di termini ordinati rispetto alla prima lettera.
Inverting: Il processo di inverting si occupa invece di collezionare le coppie \((\text{term}, \text{docID})\) per una data term-partition al fine di effettuare un sorting delle coppie utilizzando gli algoritmi visti nella lezione precedente e generare le posting lists. Le coppie \((\text{term}, \text{docID})\) relative ad una data term-partition possono essere generate da più parsers. L'inverter mano a mano che i vari parsers gli inviano le loro coppie si deve mettere a lavorare per costruire l'indice parziale. Gli indici parziali che vengono costruiti dagli inverters vengono poi uniti tra loro.
Questa suddivisione del task principale nei sotto-task, da noi chiamati parsing e inverting è anche legata al costo delle singoli operazioni, che può essere molto costosa. Nel nostro esempio abbiamo che i parsers fanno le coppie e gli inverters le ordinano per costruire gli indici inversi parziali.
Un esempio in cui l'indice originale è diviso in tre blocchi diversi è mostrato nel seguente schem
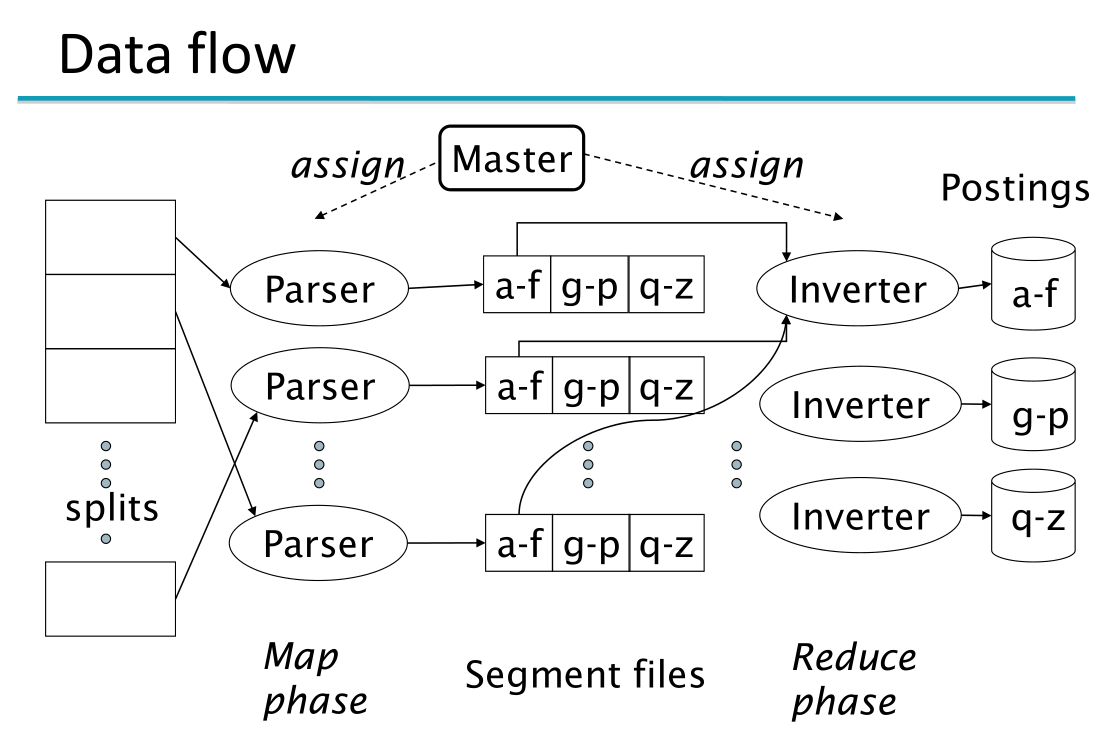
Ci possiamo quindi chiedere: a quale livello vogliamo scalare? Potremmo anche pensare di suddividere il processo in modo estremo, andando a costruire un indice inverso per ogni lettera. Arrivare a questi livello di granularità però potrebbe causare vari problemi, come ad esempio il fatto che i sistemi operativi moderni non permettono di avere un numero arbitrario di files in una directory. Si deve quindi trovare un giusto bilanciamento tra la granularità del lavoro e i benefici di performance ottenuti.
Abbiamo almeno due modi diversi per suddividere un indice tra più macchine: un primo metodo si basa sui termini, mentre un altro metodo si basa sui documenti.
Un term-partitioned distributed index è un indice distribuito partizionato in base al valore dei termini. A ciascuna macchina assegno un range di valori che rappresentano i termini che quella macchina deve gestire. Ad esempio, posso assegnare alla macchina \(1\) il range \((\text{a-f})\), mentre alla macchina \(2\) il range \((\text{g-z})\). Così facendo tutte le query contenenti parole che si trovano nel primo range vengono gestite dalla macchina \(1\), e vengono invece gestite dalla macchina \(2\) le query con parole che si trovano nel secondo range.
Anche se dividere l'indice rispetto ai termini potrebbe funzionare, non è questo l'approccio utilizzato nella pratica. Nella pratica la maggior parte delle grandi search engine preferiscono partizionare l'indice distribuito basandosi sui documenti. Tramite un procedimento di tipo MapReduce è infatti possibile trasformare un indice distribuito partizionato rispetto ai termini in un indice distribuito partizionato rispetto ai documenti.
L'approccio MapReduce non serve solamente per costruire indici inversi in modo distribuito. Esso infatti è infatti un framework generale introdotto da Jeffrey Dean e Sanjay Ghemawat nel seguente paper ed è stato introdotto al fine di implementare il calcolo distribuito su sistemi reali.
La potenza di MapReduce sta nel fatto che i singoli step di reduce() e map() sono lasciati al particolare contesto, mentre il modo in cui il calcolo viene distribuito è definito dal framework stesso.
Apache hadoop è un open-source framework che implementa meccanismi di MapReduce.
Osservazione: Possiamo pensare ad un framework come ad un insieme di soluzioni, tecniche e metodi messe a disposizioni per risolvere problemi noti.
Supponiamo di voler applicare il paradigma MapReduce per andare a calcolare la term frequency \(\text{tf})\), dei vari termini, che ricordiamo essere definita come il numero di occorrenze totali di ciascun termine nei vari documenti. Per risolvere questo problema possiamo procedere assumendo che ogni parsers genera delle triple della forma
\[\text{(term, doc, occ_term)}\]
dove \(\text{occ_term}\) è il numero di occorrenze del termine \(\text{term}\) nel documento \(\text{doc}\). Una volta ottenute tutte le triple, il parser le invia ad un inverter, che avrà il compito di combinare le occorrenze dei vari termini nei vari documenti al fine di contare il numero totale di occorrenze per ogni termine.
Fino ad adesso abbiamo lavorato assumendo di lavorare con collezioni di documenti statiche. Andiamo adesso a trattare l'indicizzazione di una collezione di documenti che cambia nel tempo. Abbiamo tre diversi metodi per gestire collezioni dinamiche, che sono:
Lavorare sempre con collezioni statiche e aggiornare la nostra collezione statica, per poi indicizzare nuovamente tutto da capo.
Utilizzare due indici: uno principale, grosso, e un altro ausilario e piccolo.
Utilizzando il logarithmic merge.
Per il primo approccio non c'è molto di dire al riguardo. Osserviamo solamente che tale tecnica era la tecnica utilizzata da google nei suoi primi anni di lavoro, quando il carico era tale da rendere tale soluzione accettabile. Andiamo adesso a trattare in più dettaglio gli altri due metodi.
In questo approccio l'indice ausiliario viene utilizzato per indicizzare i documenti più recenti, mentre quello grosso contiene i documenti più vecchi.
Quando un utente fa una query, entrambi gli indici vengono utilizzati. Per gestire le operazioni di delete, al posto di eliminare subito i documenti, che sarebbe una operazione onerosa, si utilizzano delle bitmask. L'idea infatti è di filtrare i documenti cancellati quando sto rispondendo ad una query. In questo modo siamo in grado di supportare tutte le operazioni CRUD (Create, Read, Update, Delete).
Alla fine si può scegliere se re-indicizzare il tutto tutto, oppure fare il merge dei due indici. Notiamo che il merge dei due indici può essere efficiente se manteniamo un file separato per ogni posting list, in quanto basterebbe fare una append operation. Creare troppi file però non è molto efficiente nei moderni sistemi operativi.
Questo metodo assume che il tasso di documenti nuovi è abbastanza piccolo, ed era il metodo utilizzato fino a qualche anno fa. Attualmente si utilizzano degli schemi ibridi.
Dato che la creazione di vari indici ausiliari non è molto efficiente, assumiamo adesso di lavorare con un unico grande indice.
Per poter supportare le operazioni di inserimento di un documento all'interno dell'indice nel modo più efficiente possibile, dobbiamo cercare di lavorare direttamente in memoria fisica, senza passare per il disco. Ovviamente, dato che la memoria fisica è più limitata del disco in termine di spazio disponibile, ogni tanto si sarà costretti ad interagire con il disco per memorizzare i nuovi dati indicizzati. L'idea è quindi quella di minimizzare il più possibile queste interazioni col disco e renderle il più efficienti possibili.
Per fare questo si mantengono una serie di indici, ciascuno il doppio più grande del precedente. Il più piccolo di questi indici, \(Z_0\), è istanziato in memoria, mentre gli altri sono istanziati sul disco \(l_0\), \(l_1\),... .Ogni volta che \(Z_0\) diventa troppo grande, lo vado a scrivere sul disco come \(l_0\), oppure faccio il merge con \(l_0\) (se \(l_0\) è già esistente), per ottenere \(Z_1\). \(Z_1\) lo posso poi o scrivere sul disco come \(l_1\), oppure lo posso mergare con \(l_1\) (se \(l_1\) è già esistente), per ottenere \(Z_2\), e via dicendo.
Questo procedimento è descritto dal seguente algoritmo

Il logarithmic merge ci permette di diminuire il numero di merge, andando comunque a limitare il numero di indici ausiliari utilizzati. In particolare il numero di merge cresce in modo logaritmico al crescere del size totale del mio indice. Sia \(T\) il numero totale dei postings e sia \(n\) il size dell'indice ausiliario, allora ho che
Utilizzando lo schema con un indice principale e uno ausilario, la costruzione dell'indice necessita tempo \(O(T^2/n)\).
Utilizzando il log merge invece ho un costo di \(O(T \cdot \log T)\), in quanto effettuo \(O(\log T)\) merge, e ciascun merge necessita di \(O(T)\).
Il query processing time invece è aumentato, in quanto posso avere \(O(\log T)\) diversi indici, e quindi per rispondere alla query potrei dover fare il merge di \(O(\log T)\) indici.
Il logarithmic merge può essere implementato sugli inverter nello schema MapReduce visto precedentemente e può dire agli inverter come scrivere sul disco.
Osservazione 1: Se il tasso di documenti è abbastanza alto, è possibile far vedere che le statistiche relative agli indici più grandi sono abbastanza significative rispetto a tutti quanti gli indici.
Osservazione 2: Come faccio a definire un indice che sia performante su tempistiche estremamente veloci, e che sia in grado, per esempio, di trovare gli ultimi tweet? L'idea base è quella di scrivere i dati, non dal primo all'ultimo, ma dall'ultimo al primo. In certi contesti, come twitter, non mi interessa nemmeno di costruire una funzione di ranking, dato che la rilevanza di un tweet è principalmente data dal numero di hashtags.