IR - 04 - Compression I
Data:
Sito corso: link
Slides: IR - Slides - 03 Compression.pdf
In questa lezione abbiamo cominciato a vedere le prime tecniche utilizzate per comprimere gli indici inversi, con un particolare focus per la compresione del dizionario.
Uno schema di compressione, per poter essere applicato nel campo dell'IR, deve rispettare almeno le seguenti richieste:
Lossless compression: Non ci deve essere perdita di informazioni
Decodifica efficiente: Il tempo per leggere i dati compressi e rimuovere la compressione deve essere minore del tempo necessario a leggere i dati non compressi.
Se queste richieste non sono rispettate da un particolare schema di compressione, allora non ha senso utilizzare quello schema, in quanto non porterebbe a nessun beneficio significativo.
NOTA BENE: Prima di iniziare è importante premettere che le tecniche che andremo a descrivere devono sempre essere utilizzate in modo critico, e a seconda del contesto potrebbe essere necessario combinare tra loro tecniche di compressione diverse.
Una compressione è detta lossless quando tutte le informazioni contenute nel dato compresso sono mantenute. In IR utilizziamo esclusivamente compressioni lossless. Esistono però altre tipologie di compressione, come quella jpeg, che sono lossy.
Alcuni step nel processamento dei documenti per la creazione dell'indice possono essere di tipo lossy, come ad esempio quando andiamo ad eliminare le stop-words, oppure quando facciamo case folding. Tra queste tecniche troviamo anche le seguenti
No numbers: rimuovo i numeri.
Case folding: non considero le maiuscole.
30 stopwords: rimuovo le top 30 stopwords.
150 stopwords: rimuovo le top 150 stopwords.
stemming:
In termine di compressione ci vogliamo concentrare su due aspetti della nostra struttura dati principale: il dizionario e le posting lists. A tale fine può essere utile ricordare le seguenti leggi empiriche.
Anche se il dizionario non contiene troppe parole, la sua dimensione cresce comunque rispetto alla dimensione della collezione. In generale, se abbiamo al più parole di 20 caratteri, un possibile upper bound per il dizionario è \(70^{20} \approx 10^{37}\), dove \(70\) è la dimensione dell'alfabeto con cui costruiamo le nostre parole.
Esiste poi una legge empirica, chiamata Heap's law, che ci permette di relazionare la dimensione del dizionario alla dimensione della collezione. La legge in particolare ci dice che, denotato con \(\text{M}\) il size del dizionario e con \(\text{T}\) il numero di tokens nella collezione, abbiamo che
\[M = kT^b\]
dove valori tipici per \(k\) sono \(30 \leq k \leq 100\), e \(b \approx 0.5\). Tramite questa legge siamo quindi in grado di stimare approssimatamente il size del vocabolario sapendo il numero di tokens nella collezione.
Esempio: Se consideriamo il dataset RCV1 (Reuters dataset), già introdotto in una lezione precedente, abbiamo che la legge di Heap riesce ad approssimare molto bene la relazione tra la dimensione del dizionario e la dimensione della collezione. Il seguente grafico mostra come la retta tratteggiata, ottenuta dalla legge di Heap con i paramatri \(k=10^{1.64}, b=0.49\), approssima sempre meglio la relazione tra la dimensione del dizionario e quella della collezione al crescere del numero di tokens.
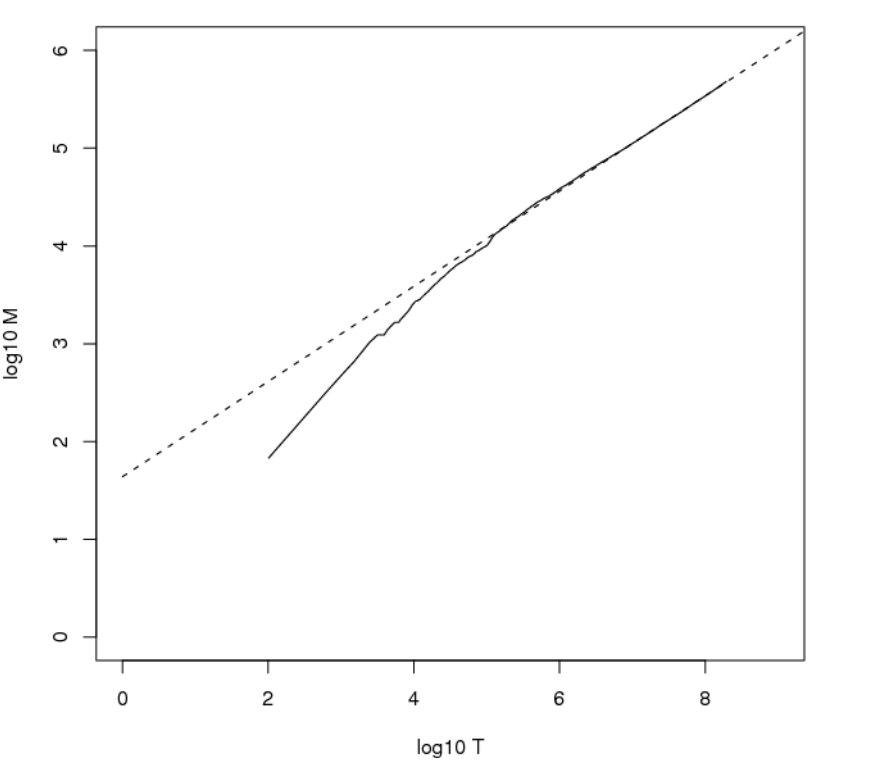
Lo spazio occupato dalle posting lists dipende, tra le tante cose, anche dalla frequenza dei token nei vari documenti. In particolare, più frequente è un token, e più sarà presente in vari documenti, e quindi più \(\text{docIDs}\) dovrò memorizzare nella postings list di quel token.
La legge di Zipf (Zipf's law) può essere utilizzata per stimare la frequenza relativa di ogni termine. Essa ci dice che nei linguaggi naturali ci sono, tendenzialmente, poche parole con una elevata frequenza, e tante parole con una frequenza molto più bassa. Volendo essere più precisi, la legge afferma che ordinando i tokens per frequenza dal più frequente al meno frequente, si stima che l' \(i\) esimo termine più frequente ha una frequenza proporzionale a \(1/i\). In particolare
\[\text{cf}_i \approx \frac{1}{i} = \frac{K}{i}\]
dove \(K\) è una costante di normalizzazione, mentre \(\text{cf}_i\) indica la collection frequency dell' \(i\) esimo termine più frequente nella collezione.
Una conseguenza della legge di Zipfs è che se il termine più frequente appare \(\text{cf}_1\) volte, allora il secondo termine più frequente apparirà più o meno \(\text{cf}_1/2\), il terzo termine più frequente apparirà più o meno \(\text{cf}_1/3\) volte, e via dicendo.
Le ragioni principali per cui vogliamo comprimere il dizionario sono le seguenti: come prima cosa, la ricerca nell'indice parte andando a cercare il termine nel dizionario; inoltre, il dizionario deve anche essere mantenuto in memoria. Questo ci incentiva a trovare metodi per far si che la memoria utilizzata dal dizionario sia la più piccola possibile.
Andiamo adesso a vedere delle possibili tecniche che ci permettono di comprimere il dizionario. Prima di iniziare però descriviamo brevemente la struttura dati iniziale utilizzata per memorizzare il dizionario.
Supponiamo di lavorare con un dizionario rappresentato da una tabella con delle righe a grandezza fissata e con una struttura dati di ricerca che ci permette di cercare velocemente i termini d interesse nel nostro dizionario.
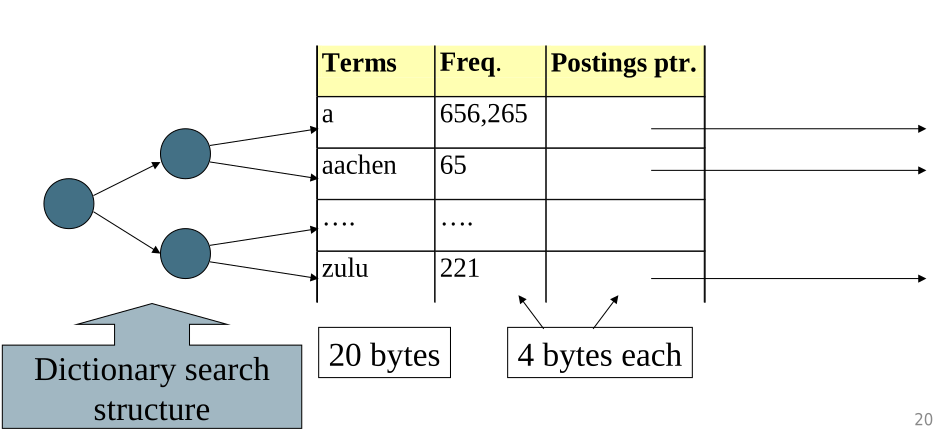
Il dizionario è quindi formato da entry con le seguenti dimensioni
Memorizzando in questo modo il dataset di Reuters abbiamo una dimensione totale di \(11.2 \text{MB}\).
Notiamo che lavorare con delle fixed-width entry porta ad un grande spreco, in quanto la maggior parte dei bytes utilizzati nella colonna dei termini sono sprecati. Per memorizzare un termine di una lettera infatti, al posto di utilizzare un solo byte, ne utilizziamo 20.
Per cercare di eliminare lo spreco di bytes utilizzati per memorizzare i termini l'idea è quella di memorizzare i termini del dizionario in una lunga stringa di caratteri. Il dizionario quindi non avrà più i termini, ma conterrà invece dei puntatori che puntano al primo carattere del relativo termine nella stringa dei termini del dizionario.
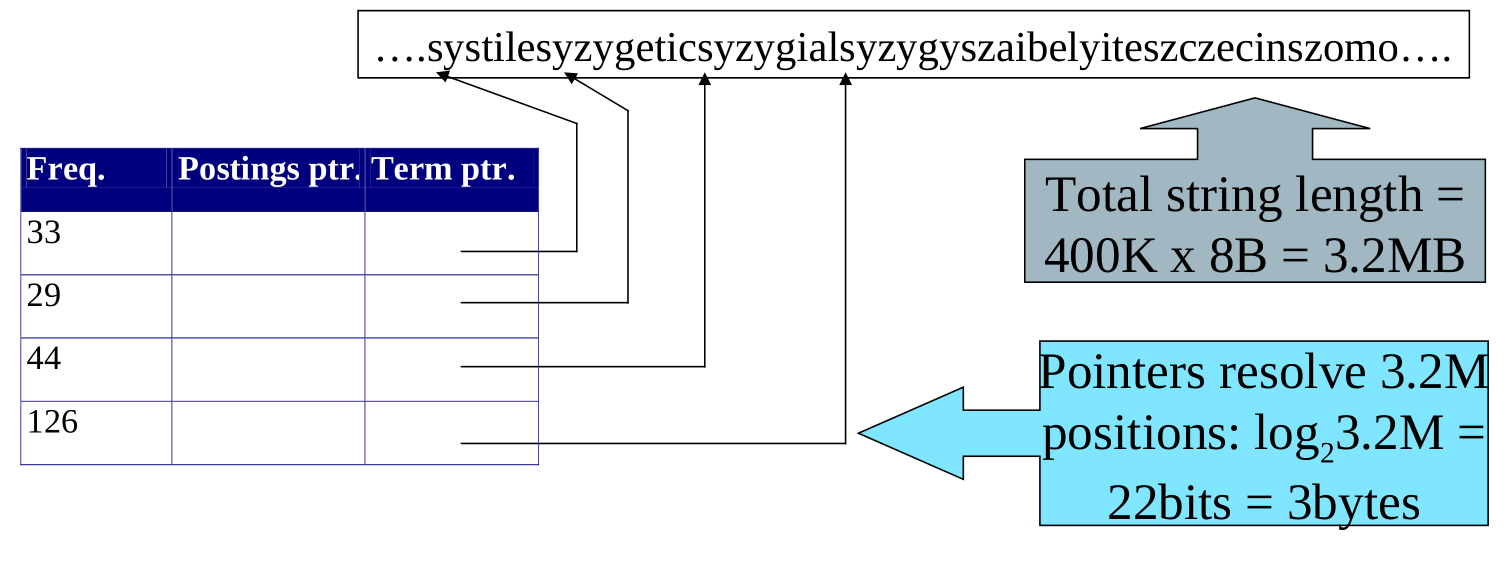
Il dizionario viene quindi modificato nel seguente modo
Nell'esempio del database Reuters, lo spazio utilizzato è quindi calcolato utilizzando i seguenti dati:
Frequenza del termine: \(4\) bytes
Pointer alla postinng list: \(4\) bytes
Term pointer: \(3\) bytes
Bytes in media per term in term string: \(8\) bytes
Dove i bytes per term pointer sono stati calcolati utilizzando la lunghezza della term string, che è \(400 \text{k} \cdot 8 \text{B} = 3.2 \text{MB}\).
In totale quindi il dizionario è memorizzato con
\[400 \text{k} \cdot 19 = 7.6 \text{MB}\]
Notiamo come non siamo stati in grado di risparmiare molto, in quanto adesso, oltre a memorizzare i termini, dobbiamo anche memorizzare i puntatori per capire dove si trova il termine all'interno della term-string.
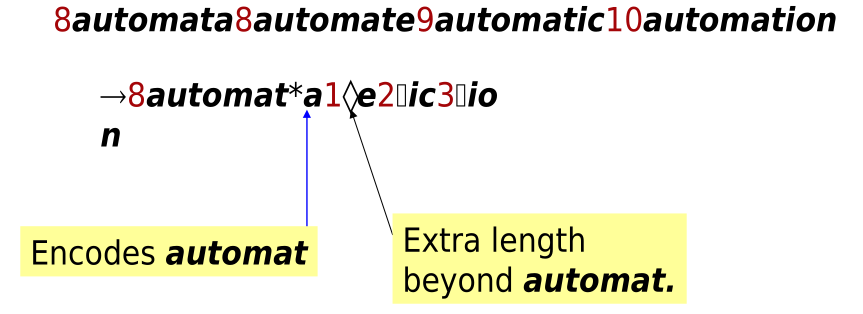
Il blocking consiste nel prendere la struttura descritta prima, ma al posto di memorizzare ogni puntatore, andiamo a memorizzare i puntatori solamente per ogni \(k\) -esimo termine, dove \(k\) è detto block size. Per capire dove una stringa finisce quindi necessitiamo di memorizzare, assieme ai termini, le lunghezze dei termini stessi, il che richiede uno o due bytes extra.
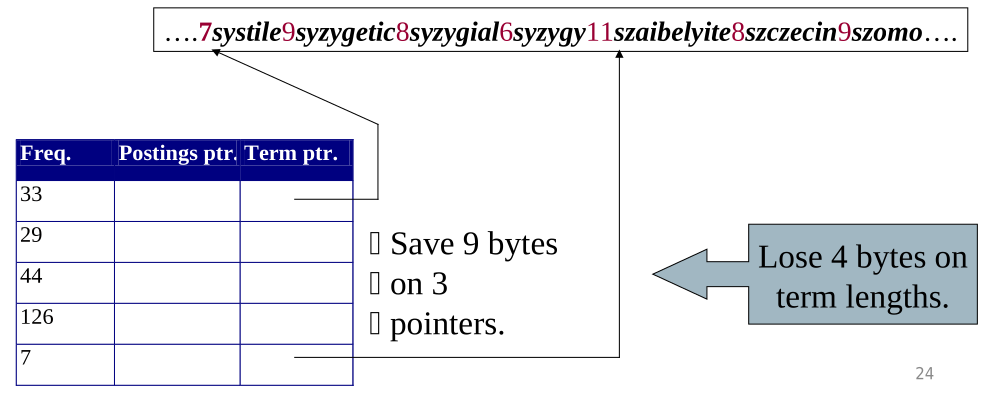
Così facendo la stringa che rappresenta il dizionario ha la seguente forma,
\[\text{7systile9syzygetic8syzygial6syzygy11szaibelyite8szczecin9szomo}\]
dove le lunghezze delle stringhe non vengono memorizzate come numeri, ma vengono espresse come caratterti. Questo viene fatto per risparmiare spazio, in quanto memorizzare un intero richiederebbe 4 bytes in architetture a 32 bit.
In generale più grande è il block size \(k\) e più sarà lo spazio risparmiato. Il costo di avere un block size elevato però viene pagato con il tempo necessario per trovare la parola: più \(k\) è grande e più sarà grande la parte di stringa che devo scorrere lineramente ad ogni ricerca.
Nel dataset di Reuters, con un block size \(k=4\) abbiamo che se prima utilizzavamo \(3\) bytes per ogni \(4\) records, per un totale di \(12\) bytes per \(4\) records, adesso utilizziamo solamente \(3 + 4 = 7\) bytes. Abbiamo quindi i seguenti costi di occupazione della memoria
Total bytes for freq: \(400k \times 4\)
Total bytes for pointer to postings list: \(400k \times 4\)
Total bytes for term pointers: \(100k \times 7\)
Total bytes for term in term string: \(400k \times 8\)
che se sommati danno un totale di
\[400k \times 4 + 400k \times 4 + 100k \times 7 + 400k \times 8 = 7.1 \text{MB}\]
Esercizio: Stimare lo spazio utilizzare con il blocking per i block size di \(k = 4, 8\) e \(16\), e notare lo spazio salvato.
Notiamo che senza fare il blocking il dizionario, che è rappresentato da una struttura alborea, fa un determinato numero di confronti.
È poi possibile stimare il numero medio di confronti effettuati andando a calcolare, per ogni parola, il numero di confronti necessari per arrivare a quella parola, e dividere per il numero totale delle parole.
\[\text{Avg comparisons} = \sum_{i} \frac{\text{# comparisons for term i }}{\text{# total terms}}\]
Se invece effettuiamo il blocking, allora inizialmente abbiamo comunque una binary search, ma poi ad un certo punto continuiamo con una ricerca lineare. Notiamo come scegliere \(k\) abbastanza piccolo non fa cambiare di tanto il numero medio di confronti.
Il front coding viene utilizzato per comprimere parole che hanno un lungo prefisso in comune. L'idea quindi è quella di memorizzare solo le differenze rispetto al prefisso condivisso.
Notiamo che per utilizzare questo approccio devo aver eliminato i numeri dal mio dizionario, in quanto gli unici numeri presenti devono rappresentare solo le continuazioni a partire dallo stesso prefisso.
Le posting lists, che sono liste di \(\text{docIDs}\), sono molto più grandi del dizionario. La compressione delle posting lists si basa su delle tecniche che cercano di utilizzare il numero minore di bytes possibili per rappresentare i \(\text{docIDs}\).
Consideriamo il dataset di Reuters, con i suoi 800.000 documenti. Se utilizziamo un \(\text{docID}\) di 4 bytes, siamo in grado di identificare ogni singolo documento. Quello che vogliamo fare però è utilizzare meno di \(4\) bytes per rappresentare ciascun documento.
In generale abbiamo due possibili modi per gestire le postings lists:
Le posting lists associate a termini poco frequenti, come il termine \(\text{arachnocentric}\), vengono gestite andando ad utilizzare il numero di bits necessario per indicizzare ogni doc. Nel caso di reuters questo equivale a 20 bits.
Le posting lists associate a termini molto frequenti vengono invece rappresentate come bitmap vectors. Notiamo infatti che sarebbe estremamente inefficiente memorizzare ogni doc con 20 bits.
Ricordiamo che per rispondere alle query in modo efficiente inseriamo i \(\text{docIDs}\) in modo ordinato nelle varie posting lists. Una prima idea di compressione delle posting lists si basa quindi su un cambio di rappresentazione: al posto di avere un sistema di riferimento assoluto per i vari \(\text{docIDs}\), passiamo ad uno relativo, andando a memorizzare solamente i gaps tra i vari identificativi, e non il valore assoluto.
Consideriamo il termine \(\text{computer}\), e vediamo la differenza tra un riferimento assoluto ad uno relativo
\[\begin{split} \text{absolute} &\longrightarrow 33, \,\,\, 47, \,\,\, 154, \,\,\, 159, \,\,\, 202 \\ \text{relative} &\longrightarrow 33, \,\,\, 14, \,\,\, 107, \,\,\, 5, \,\,\, 43 \\ \end{split}\]
Con questo cambiamento di rappresentazione non stiamo perdendo informazione, in quanto per capire qual è il docID nella \(i\) esima posizione della nuova lista contenente i gaps, ci basta solamente sommare tutte i valori presenti nella lista fino all' \(i\) esimo. La speranza è che la maggior parte dei gaps può essere memorizzata con meno di 20 bits. Questa tecnica porta i migliori risultati quando viene applicata alle posting lists associate a termini che non sono né eccessivamente presenti e né eccessivamente non presenti.