IR - 06 - Ranking I
Data:
Sito corso: link
Slides: IR - Slides - 04 Ranking I
Argomenti:
Ranking Retrieval
Jaccard Coefficient
Term frequency
Document frequency
tf-idf weight
Vector Space Model
In questa lezione abbiamo introdotto il problema del ranking retrieval.
In un Boolean Search Model (BSM), un documento può solamente o matchare o non matchare una data query. Questa natura binaria porta a varie conseguenze.
Per iniziare, scrivere le giuste query utilizzando gli operatori booleani
\[\text{AND}, \text{OR}, \text{ NOT}\]
che ritornano il giusto numero di documenti rispetto all'information need dell'utente è una operazione molto complessa, e può essere gestita in modo adeguato solamente da utenti esperti, e non dalla maggior parte degli utenti.
Un'altra conseguenza della natura binaria del modello è il fatto che molto spesso può succedere di avere o troppi risultati, oppure troppo pochi. Nel caso in cui abbiamo troppi risultati, a meno che questi documenti non sono trattati da una applicazione, risulta difficile gestirli tutti da un utente medio. Viceversa, nel caso in cui ne abbiamo troppo pochi, non siamo in grado di soddisfare l'information need dell'utente. Questo problema è noto con il nome di "Feast or Famine". Per gestire questo problema quindi l'utente deve gestire il numero di \(\text{AND}\) e il numero di \(\text{OR}\) all'interno della query. Troppi \(\text{AND}\) portano a pochi documenti, mentre troppi \(\text{OR}\) portano a troppi documenti.
Per cercare di risolvere le problematiche derivanti dall'utilizzo di un boolean search model è stata introdotta l'idea del ranking, che consiste nell'assegnare, per ogni query effettuata dall'utente, un valore di ranking ad ogni documento. Questo ranking intuitivamente esprime la rilevenza del documento rispetto alla query. Una volta che questi ranking sono stati assegnati è possibile ritornare i documenti ordinandoli rispetto al ranking a loro assegnato. L'idea di ordinare i documenti rispetto al ranking fu una delle prime innovazioni introdotte da Google nel campo delle search engines.
Osservazione: Notiamo che per implementare questi sistemi di ranking devono essere affrontati importanti problemi algoritmici importanti, tra i quali troviamo:
Come assegno ai documenti gli scores, nel caso di collezioni di documenti enormi?
Come ordino i documenti, sempre nel caso di collezioni di documenti enormi?
Per via dell'elevata quantità di documenti, nei sistemi moderni questi problemi non possono essere risolti in modo ottimale. Si cercano quindi delle euristiche che permettono di ottenere delle buone approssimazioni.
Consideriamo una coppia \((\text{query}, \text{doc})\). Come facciamo ad assegnare uno rank a questa coppia? Per rispondere a questa domanda possiamo utilizzare le seguenti osservazioni:
Se nessun termine della query appare nel documento, tale score deve intuitivamente essere \(0\).
Dato un termine presente nella query, al crescere della frequenza del termine nel documento, lo score deve crescere.
Al crescere del numero di termini della query che sono presenti anche nel documento, lo score deve crescere.
Utilizzando queste "linee-guida" base, possiamo definire varie funzioni matematiche che ci permettono di calcolare il ranking.
Consideriamo due insiemi \(A\) e \(B\). Il coefficiente di Jaccard è definito come il rappporto tra la cardinalità dell'intersezione e la cardinalità dell'unione dei due insiemi. In formula,
\[ \text{Jaccard}(A, B) = \frac{| A \cap B |}{| A \cup B |}\]
Notiamo che almeno uno dei due insiemi deve essere diverso dall'insieme vuoto. Alcuni valori particolari del coefficiente di Jaccard sono:
\(\text{Jaccard}(A, A) = 1\)
\(\text{Jaccard}(A, B) = 0 \text{ if } A \cap B = 0\)
Utilizzando il coefficiente di Jaccard siamo quindi sempre in grado di assegnare un numero tra \(0\) e \(1\) a una coppia di insiemi. In particolare poi questo numero cresce al crescere degli elementi in comune tra i due insiemi.
Esempio: Consideriamo la query \(q\) e il documento \(d\) dati da
\[\begin{split} q &= \text{"ides of March"} \\ q &= \text{"Caesar died in March"} \\ \end{split}\]
Utilizzando un approccio bag of words (discusso a seguire), in cui sia i documenti che le query vengono visti come dei multi-insiemi di termini è possibile il coefficiente di jaccard della coppia query-documento, che in particolare è dato da
\[\text{Jaccard}(q, d) = \frac{| \{\text{March}\} | }{ \{|\text{ideas}, \text{of}, \text{March}, \text{died}, \text{Caesar}, \text{in}|\}} = \frac16\]
Un problema fondamentale del coefficiente di Jaccard è che non tiene conto della frequenza dei termini.
Ricordiamo che, utilizzando nozioni riprese dalla teoria delle informazioni (information theory), i termini più rari sono anche quelli che contengono più informazione, mentre quelli più frequenti contengono meno informazione. Tutto questo non viene preso in considerazione utilizzando il coefficiente di Jaccard.
Anche il tipo di normalizzazione utilizzata con Jaccard può essere migliorata.
Supponiamo di considerare solo delle one-term query, ovvero delle query formate da un solo termine. Abbiamo vari modi per rappresentare la nostra collezione di documenti. Tra questi troviamo:
Binary incidence matrix: Ogni documento è rappresentato da un vettore binario.
Count Matrix: Ogni documento è rappresentato da un count vector.
Consideriamo poi un modello bag of words, caratterizzato dal fatto che non si preoccupa del particolare ordine in cui i termini appaiono nel documento, ma che tiene conto solo della loro presenza ed eventualmente del numero di occorrenze di ciascun termine in ciascun documento. Definiamo quindi la term fequency del termine \(t\) nel documento \(d\), indicata con \(\text{tf}_{t, d}\), come il numero di volte in cui \(t\) occorre in \(d\).
Cerchiamo ora di utilizzare questa quantità per andare a calcolare il ranking da assegnare ad ogni coppia \((\text{query}, \text{doc})\). Come facciamo a fare questo?
Una prima idea potrebbe essere quella di utilizzare la \(\text{tf}\) stessa, senza ulteriori trasformazioni. Notiamo però che utilizzare direttamente la raw term frequency non è una soluzione ideale, in quanto la rilevenza di un documento non cresce in modo lineare con il crescere della frequenza di un termine. Infatti, un documento con \(\text{tf} = 10\), è si più rilevante di un documento con \(\text{tf} = 1\), ma non dieci volte più rilevante.
Una seconda idea, questa volta più sensata, è quella di far crescere lo score di una coppia in modo logaritmico rispetto alla term fequency. In particolare si definisce
\[ w_{t, d} = \begin{cases} 1 + \log{(\text{tf}_{t, d})} \,\,\,\,&,\,\,\,\, \text{tf}_{t, d} > 0 \\ 0 &,\,\,\,\, \text{ else} \\ \end{cases}\]
Così facendo abbiamo definito lo score per una coppia \((\text{term}, \text{doc})\), coprendo il caso in cui la query è composta da un solo termine. Ci manca quindi da coprire il caso in cui la query è composta da più termini.
Per definire lo score di una coppia \((\text{term}, \text{doc})\) nel caso in cui la query è composta da più termini l'idea è quella di sommare lo score della coppia per ogni termine presente sia nella query che nel documento. In particolare definiamo
\[ \text{tf-matching-score}(q, d) = \sum\limits_{t \in q \cap d} w_{t, d}\]
Notiamo che questa formalizzazione rispetta tutte le nozioni su cui avevamo riflettuto precedentemente.
Con il ranking introdotto prima utilizziamo solo la loro frequenza per calcolare il ranking. In particolare quindi non scaliamo l'importanza di un termine in base a quanto raro è il termine. Questo non è ideale, in quanto tipicamente sono proprio i termini rari quelli che contengono più informazioni. Un documento che condivide con la query un termine raro sarà dunque più rilevante rispetto ad un altro documento che non lo contiene.
Il concetto di "rarità" di un termine può essere formalizzato utilizzando la frequenza del termine rispetto all'intera collezione di documenti. Così facendo si lavora quindi con due tipi di frequenze:
La term frequency, che avevamo indicato con \(\text{tf}_{t, d}\) e che indica la frequenza del termine \(t\) nel documento \(d\).
La document frequency, che indichiamo con \(\text{df}_t\) e che indica il numero di documenti che contengono il termine \(t\) rispetto all'intera collezione documentale.
L'idea è quindi quella di assegnare dei pesi maggiori ai termini rari e dei pesi più bassi, ma comunque positivi, ai termini più comuni. Per aggiungere questa ulteriore pesature utilizzo la document frequency.
In particolare sia \(\text{df}_t\) la document frequency del termine \(t\). Notiamo che \(\text{df}_t\) è una misura inversa del contenuto informativo del termine \(t\): più è alta, e più comune è \(t\), e quindi meno informazioni contiene l'eventuale presenza del termine \(t\). Sia \(N\) il numero di documenti nella collezione. Definiamo il peso associato al termine \(t\) rispetto alla sua document frequency come segue
\[\text{idf}_t = \log { \frac{N}{\text{df}_t} } \]
dove il termine \(\text{idf}\) sta per inverse document frequency, ed è una misura del "contenuto informativo" del termine. Analogamente a quanto visto prima, utilizziamo la funzione log per smorzare l'effetto dell'idf di base. L'aggiunta dell'idf ha un effetto molto limitato per le query con un solo termine.
Abbiamo adesso tutto quello che ci serve per definire uno degli schemi più semplici e utilizzati per pesare coppie \((\text{query}, \text{doc})\). Tale schema prende il nome di pesatura tf-idf, ed è definito come segue: ad ogni termine \(t\) in ogni documento \(d\) possiamo assegnare il suo peso tf-idf, definito come segue
\[w_{t, d} := (1 + \log\text{tf}_{t, d}) \cdot \log{\frac{N}{\text{df}_t}}\]
notiamo come il peso tf-idf è ottenuto moltiplicando la versione scalata della term frequency con la versione scalata della inverse document frequency.
Osservazione: Una variante della pesatura tf-idf viene utilizzata nel noto sistema IR chiamato elasticsearch.
Utilizzando la pesatura tf-idf possiamo definire la weight matrix per una collezione di documenti.
La costruzione della weight-matrix non necessita il riferimento alla query, e può essere calcolata in una fase di pre-processamento. Una volta che abbiamo costruito la nostra weight-matrix, abbiamo vari approcci per rispondere alle query degli utenti. Due di questi sono descritti a seguire:
Per ogni documento sommiamo i valori associati ai termini presenti nella query. Il documento con la somma maggiore sarà quello più rilevante. Notiamo come questo tipo di approccio non è normalizzato rispetto alla lunghezza dei documenti. Facendo la somma documenti più lunghi, solo per il fatto di essere più lunghi, hanno inevitabilmente più peso, e quindi più rilevenza, rispetto ai documenti più brevi.
Un altro approccio è l'utilizzo del Vector Space Model, che sarà il focus della parte finale della lezione.
Sia \(V\) il numero di termini. Tramite la weight matrix siamo in grado di vedere ogni documento \(d\) come un vettore di numeri reali, con una componente per ogni termine distinto del vocabolario, composto dal peso tf-idf di ogni termine presente nel documento \(d\). In particolare quindi possiamo considerare uno spazio \(|V|\) dimensionale, dove i termini sono gli assi dello spazio e i documenti sono punti, o vettori, in questo spazio. Quanto fatto per i vettori può anche essere fatto per la query, ovvero possiamo vedere le query come vettori, o punti, nello stesso spazio \(|V|\) dimensionale. Questo modello di rappresentazione prende il nome di Vector Space Model.
Utilizzando il vector space model siamo in grado di effettuare il ranking dei documenti utilizzando il concetto di somiglianza tra i vettori che rappresentano i documenti e il vettore che rappresenta la query. A tale fine risulta fondamentale la seguente osservazione
\[\text{similarity} = \text{proximity} \approx \text{negative distance}\]
Dunque, se utilizziamo una qualche norma vettoriale, come ad esempio la distanza euclidea, per misurare la distanza dei vettori, siamo anche in grado di misurare una approssimazione della loro prossimità, e dunque della loro similarità. Così facendo siamo in grado di effettuare un ranking dei documenti rispetto ad una query.
Concludiamo la lezione notando che la distanza euclidea non è molto utile per i nostri scopi, in quanto prende molto in considerazione la lunghezza dei vettori in considerazione, e può essere molto grande semplicemente perché i vettori hanno diverse lunghezze. In particolare può succedere di avere due punti che sono considerati come essere molto distanti rispetto alla distanza euclidea ma che hanno una distribuzione di termini molto simile tra loro.
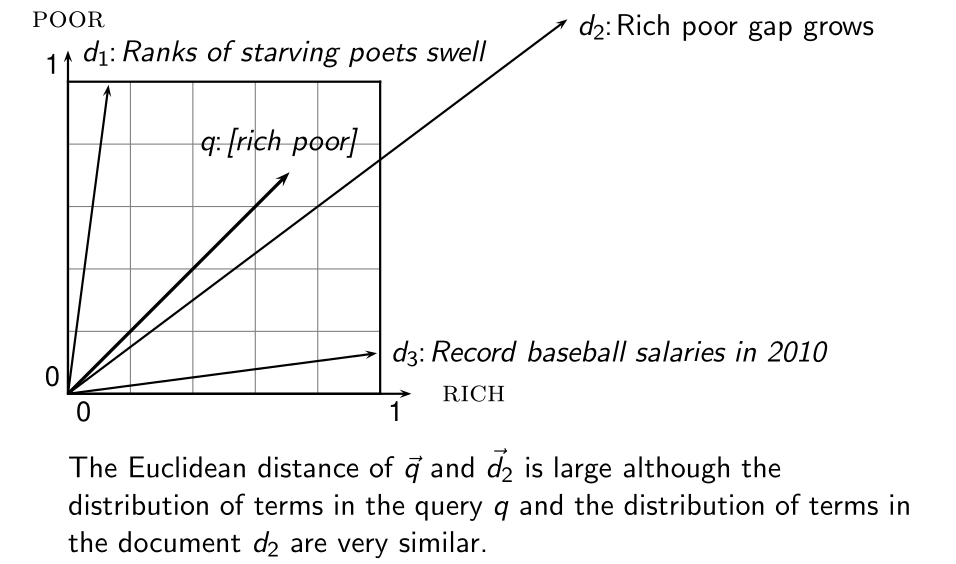
Nella prossima lezione andremo a vedere la cosine similarity, che ci offre un concetto di similarità migliore per effettuare questo tipo di ranking, in quanto non misura la similarità tramite l'inverso della distanza tra i due vettori ma bensì utilizzando l'angolo sotteso.